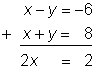El método de eliminación
Objetivos de aprendizaje
· Resolver un sistema de ecuaciones cuando no es necesaria la multiplicación para eliminar una variable.
· Resolver un sistema de ecuaciones cuando es necesaria la multiplicación para eliminar una variable.
· Reconocer sistemas que no tienen solución o que tienen un número infinito de soluciones.
· Resolver problemas de aplicación usando el método de eliminación.
Introducción
El método de eliminación para resolver sistemas de ecuaciones lineales usa la propiedad de la igualdad de la suma. Puedes sumar el mismo valor a cada lado de la ecuación.
Entonces si tienes un sistema: x – 6 = −6 y x + y = 8, puedes sumar x + y al lado izquierdo de la primera ecuación y suma 8 a la derecha de la ecuación. Y como x + y = 8, estas sumando el mismo valor a cada lado de la primera ecuación.
Si sumas las dos ecuaciones, x – y = −6 y x + y = 8 como explicamos arriba, observa lo que pasa.
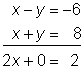
Has eliminado el término y y esta ecuación puede resolverse usando los métodos para resolver ecuaciones con una variable.
Veamos cómo se resuelve este sistema usando el método de eliminación.
| Ejemplo | ||||
| Problema | Usa eliminación para resolver el sistema. x – y = −6 x + y = 8 |
| ||
|
|
| Suma las ecuaciones. | ||
|
| 2x = 2 x = 1 | Resuelve x. | ||
|
| x + y = 8 1 + y = 8 y = 8 – 1 y = 7 | Sustituye x = 1 en una de las ecuaciones originales y resuelve y. | ||
|
| x – y = −6 1 – 7 = −6 −6 = −6
VÁLIDO | x + y = 8 1 + 7 = 8 8 = 8
VÁLIDO | ¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos. | |
| Respuesta | La solución es (1, 7). |
| ||
Desafortunadamente no todos los sistemas resultan tan fáciles. Por ejemplo, un sistema como 2x + y = 12 y −3x + y = 2. Si usamos estas ecuaciones, no se elimina ninguna variable.
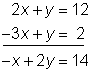
Pero quieres eliminar una variable. Por lo que sumas el opuesto de una de las ecuaciones con la otra ecuación.
2x + y =12 → 2x + y = 12 → 2x + y = 12
−3x + y = 2 → − (−3x + y) = −(2) → 3x – y = −2
5x + 0y = 10
Has eliminado la variable y, y ahora el problema puede resolverse. Veamos el ejemplo siguiente.
| Ejemplo | ||||
| Problema | Usa eliminación para resolver el sistema. 2x + y = 12 −3x + y = 2 |
| ||
|
| 2x + y = 12 −3x + y = 2 | Puedes eliminar la variable y si sumas el opuesto de una de las ecuaciones a la otra ecuación. | ||
|
| 2x + y = 12 3x – y = −2 5x = 10 | Reescribe la segunda ecuación como su opuesto. Suma. | ||
|
| x = 2 | Resuelve x. | ||
|
| 2(2) + y = 12 4 + y = 12 y = 8 | Sustituye y = 2 en una de las ecuaciones originales y resuelve y. | ||
|
| 2x + y = 12 2(2) + 8 = 12 4 + 8 = 12 12 = 12
VÁLIDO | −3x + y = 2 −3(2) + 8 = 2 −6 + 8 = 2 2 = 2
VÁLIDO | ¡Asegúrate de comprobar tu respuesta en ambas ecuaciones!
Los resultados son correctos. | |
| Respuesta | La solución es (2, 8). |
| ||
Los siguientes son dos ejemplos mostrando cómo resolver un sistema lineal de ecuaciones usando eliminación.
| Ejemplo | |||||||||||||||||||||||||||||||||||
| Problema | Usa eliminación para resolver el sistema. −2x + 3y = −1 2x + 5y = 25 | ||||||||||||||||||||||||||||||||||
|
|
| Observa los coeficientes de cada variable en la ecuación. Si sumas estas dos ecuaciones, el término x será eliminado porque −2x + 2x = 0. | |||||||||||||||||||||||||||||||||
|
|
| Suma y resuelve y. | |||||||||||||||||||||||||||||||||
|
| 2x + 5y = 25 2x + 5(3) = 25 2x + 15 = 25 2x = 10 x = 5 | Sustituye y = 3 en una de las ecuaciones originales. | |||||||||||||||||||||||||||||||||
|
| −2x + 3y = −1 −2(5) + 3(3) = −1 −10 + 9 = −1 −1 = −1
VÁLIDO | 2x + 5y = 25 2(5) + 5(3) = 25 10 + 15 = 25 25 = 25
VÁLIDO | Comprueba las soluciones.
Los resultados son correctos. | ||||||||||||||||||||||||||||||||
| Respuesta | La solución es (5, 3). |
| |||||||||||||||||||||||||||||||||
| Ejemplo | ||||||||||||||||||||||||||||
| Problema | Usa eliminación para resolver x y y. 4x + 2y = 14 5x + 2y = 16 |
| ||||||||||||||||||||||||||
|
|
| Observa los coeficientes de cada variable en cada ecuación. Necesitarás sumar el opuesto de una de las ecuaciones para eliminar la variable y, porque 2y + 2y = 4y, pero 2y + (−2y) = 0. | ||||||||||||||||||||||||||
|
|
| Cambia una de las ecuaciones por su opuesto, suma y resuelve x.
| ||||||||||||||||||||||||||
|
| 4x + 2y = 14 4(2) + 2y = 14 8 + 2y = 14 2y = 6 y = 3 | Sustituye x = 2 en una de las ecuaciones originales y resuelve y. | ||||||||||||||||||||||||||
| Respuesta | La solución es (2, 3). |
| ||||||||||||||||||||||||||
Comprueba el último ejemplo — sustituye (2, 3) en ambas ecuaciones. Obtienes dos enunciados válidos: 14 = 14 y 16 = 16!
Observa que pudiste haber usado el opuesto de la primera ecuación en lugar del de la segunda ecuación y obtenido el mismo resultado.
Muchas veces, sumar las ecuaciones o sumar el opuesto de una de las ecuaciones no resultará en la eliminación de una variable. Observa el sistema siguiente.
3x + 4y = 52
5x + y = 30
Si sumas las ecuaciones anteriores o si sumas el opuesto de una de las ecuaciones, obtendrás una ecuación que sigue teniendo dos variables. Entonces, primero usemos la propiedad multiplicativa de la igualdad. Puedes multiplicar ambos lados de las ecuaciones por un número que hará que el coeficiente de una de las variables quede opuesto a la misma variable en la otra ecuación.
Es aquí donde la multiplicación es útil. Observa que la primera ecuación contiene el término 4y, y la segunda ecuación contiene el término y. Si multiplicas la segunda ecuación por −4, cuando sumes las dos ecuaciones las variables y se sumarán para ser 0.
3x + 4y = 52 → 3x + 4y = 52 → 3x + 4y = 52
5x + y = 30 → −4(5x + y) = −4(30) → −20x – 4y = −120
−17x + 0y = −68
Veamos el siguiente ejemplo.
| Ejemplo | |||||||||||||||||||
| Problema | Resuelve x y y. Ecuación A: 3x + 4y = 52 Ecuación B: 5x + y = 30 | ||||||||||||||||||
|
|
| Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes.
| |||||||||||||||||
|
|
| Multiplica la segunda ecuación por −4 para que tengan el mismo coeficiente. | |||||||||||||||||
|
|
| Reescribe el sistema y suma las ecuaciones. | |||||||||||||||||
|
|
| Resuelve x. | |||||||||||||||||
|
| 3x + 4y = 52 3(4) + 4y = 52 12 + 4y = 52 4y = 40 y = 10 | Sustituye x = 4 en una de las ecuaciones originales para encontrar y. | |||||||||||||||||
|
| 3x + 4y = 52 3(4) + 4(10) = 52 12 + 40 = 52 52 = 52
VÁLIDO | 5x + y = 30 5(4) + 10 = 30 20 + 10 = 30 30 = 30
VÁLIDO | Comprueba tu respuesta.
Los resultados son correctos. | ||||||||||||||||
| Respuesta | La solución es (4, 10). |
| |||||||||||||||||
Existen otras maneras de resolver este problema. En lugar de multiplicar una ecuación para eliminar una variable cuando las ecuaciones se suman, pudiste haber multiplicado ambas ecuaciones por números distintos.
Ahora eliminemos la variable x. Multiplica la Ecuación A por 5 y la Ecuación B por −3.
| Ejemplo | |||||||||||||||||||||||||||||||
| Problema | Resuelve x y y. 3x + 4y = 52 5x + y = 30 |
| |||||||||||||||||||||||||||||
|
|
| Busca los términos que pueden ser eliminados. Las ecuaciones no tienen ningún término x o y con los mismos coeficientes
| |||||||||||||||||||||||||||||
|
|
| Para usar el método de eliminación, debes crear variables con el mismo coeficiente, luego puedes multiplicarlas. Multiplica la primera ecuación por 5. | |||||||||||||||||||||||||||||
|
|
| Ahora multiplica la segunda ecuación −3. | |||||||||||||||||||||||||||||
|
|
| Luego suma las ecuaciones, y resuelve y. | |||||||||||||||||||||||||||||
|
| 3x + 4y = 52 3x + 4(10) = 52 3x + 40 = 52 3x = 12 x = 4 | Sustituye y = 10 en una de las ecuaciones originales para encontrar x. | |||||||||||||||||||||||||||||
| Respuesta | La solución es (4, 10). | Llegas a la misma solución que antes. | |||||||||||||||||||||||||||||
Estas ecuaciones fueron multiplicadas por 5 y −3 respectivamente, porque eso te daba los términos que suman 0. Asegúrate de multiplicar todos los términos de la ecuación.
| Félix necesita encontrar x y y del siguiente sistema. Ecuación A: 7y − 4x = 5 Ecuación B: 3y + 4x = 25
Si quiere usar el método de eliminación para eliminar una de las variables, ¿cuál es la manera más eficiente de hacerlo?
A) Sumar la Ecuación A y la Ecuación B
B) Sumar 4x a ambos lados de la Ecuación A
C) Multiplicar la Ecuación A por 5
D) Multiplicar la Ecuación B por −1
|
Al igual que con el método de sustitución, el método de eliminación a veces elimina ambas variables y te quedas con un enunciado válido o inválido. Recuerda que un enunciado inválido significa que no hay solución.
Veamos otro ejemplo.
| Ejemplo | ||
| Problema | Resuelve x y y. -x – y = -4 x + y = 2 |
|
|
| -x – y = -4 x + y = 2 0 = −2 | Suma las ecuaciones para eliminar el término x. |
| Respuesta | No hay solución. |
|
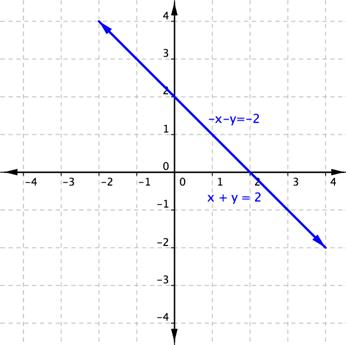
Graficar estas rectas muestra que son paralelas y como tales no comparten ningún punto, verificando que no hay solución.
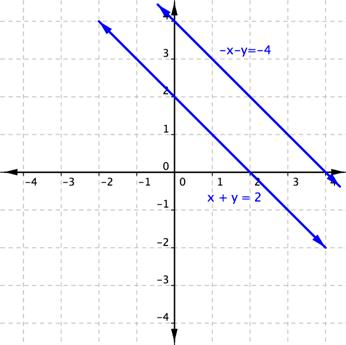
Si ambas variables son eliminadas y te quedas con un enunciado válido, significa que hay un número infinito de pares ordenados que satisfacen ambas ecuaciones. De hecho, las ecuaciones son la misma recta.
| Ejemplo | ||
| Problema | Resuelve x y y. x + y = 2 -x − y = -2 |
|
| x + y = 2 -x − y = -2 0 = 0 | Suma las ecuaciones para eliminar el término x. | |
| Respuesta | Hay un número infinito de soluciones. | |
Graficar estas dos ecuaciones te ayudará a ilustrar lo que está sucediendo.
El método de eliminación puede aplicarse para resolver sistemas de ecuaciones que modelan situaciones del mundo real. Dos ejemplos del uso del método de eliminación se muestran a continuación.
| Ejemplo | |||
| Problema | La suma de dos números es 10. La resta es 6. ¿Cuáles son estos números? | ||
|
| x + y = 10 x – y = 6 | Escribe un sistema de ecuaciones para modelar la situación. x = un número y = el otro número | |
|
| x + y = 10 + x – y = 6 2x = 16 x = 8 | Suma las ecuaciones para eliminar el término y y luego resolver x. | |
|
| x + y = 10 8 + y = 10 y = 2 | Sustituye el valor por x en una de las ecuaciones originales para encontrar y. | |
|
| x + y = 10 8 + 2 = 10 10 = 10
VÁLIDO | x – y = 6 8 – 2 = 6 6 = 6
VÁLIDO | Comprueba tu respuesta sustituyendo x = 8 y y = 2 en el sistema original.
Los resultados son correctos. |
| Respuesta | Los números son 8 y 2. | ||
| Ejemplo | ||||
| Problema | Un teatro vendió 800 boletos para el espectáculo del viernes en la noche. Un boleto de niño cuesta $4.50 y un boleto de adulto cuesta $6.00. LA cantidad total recolectada fue de $4,500. ¿Cuantos boletos de vendieron de cada tipo? | |||
|
| El número total de boletos vendidos es 800. a + c = 800 La cantidad de dinero recolectado es $4,500 6a + 4.5c = 4,500
Sistema de ecuaciones: a + c = 800 6a + 4.5c = 4,500 | Escribe un sistema de ecuaciones para modelar la situación de la venta de boletos. a = número de boletos de adulto vendidos c = número de boletos de niño vendidos | ||
|
| 6(a + c) = 6(800) 6a + 4.5c = 4,500
6a + 6c = 4,800 6a + 4.5c = 4,500 | Usa la multiplicación para reescribir la primera ecuación.
| ||
|
| 6a + 6c = 4,800 −6a – 4.5c = −4,500 1.5c = 300
c = 200 | Suma el opuesto de la segunda ecuación para eliminar el término y resolver c. | ||
|
| a + 200 = 800 −200 −200 a = 600 | Sustituye 200 por c en una de las ecuaciones originales. | ||
|
| a + c = 800 600 + 200 = 800 800 = 800
VÁLIDO
| 6a + 4.5c = 4,500 6(600) + 4.5(200) = 4,500 3,600 + 900 = 4,500 4500 = 4,500
VÁLIDO | Comprueba tu respuesta sustituyendo a = 600 y c = 200 en el sistema original. Los resultados son correctos. | |
| Respuesta | Se vendieron 600 boletos de adulto y 200 boletos de niño. |
| ||
Sumario
La combinación de ecuaciones es una herramienta útil para resolver sistemas de ecuaciones. A la suma o resta de dos ecuaciones con el fin de eliminar una variable común se le llama método de eliminación (o suma). Una vez que una variable ha sido eliminad, es mucho más fácil resolver la otra variable. La multiplicación se puede usar para obtener términos semejantes en ecuaciones antes de combinarlas. Cuando usamos el método de multiplicación, es importante multiplicar todos los términos a ambos lados de la ecuación, no sólo el término que estás tratando de eliminar.