El método de sustitución

 

Objetivos de Aprendizaje

·         Resolver un sistema de ecuaciones usando el método de sustitución.

·         Reconocer sistemas de ecuaciones que no tienen solución o que tienen un número infinito de soluciones.

·         Resolver problemas de aplicación usando el método de sustitución.

 

Una gráfica puede usarse para mostrar la solución de un sistema de ecuaciones lineales. Sin embargo, determinar la solución de manera precisa a partir de una gráfica no siempre es fácil. Por ejemplo ¿dónde crees que las dos rectas siguientes se intersectan?

 

 

Parece que se intersectan en (1.8, –0.7) — aunque esto es sólo un estimado. En casos como este, puedes usar métodos algebraicos para encontrar soluciones exactas. Un método para esto es el método de sustitución. Resuelves la variable de una ecuación y luego sustituyes esta expresión en la otra ecuación.

 

En el método de sustitución resuelves una variable y luego sustituyes esa expresión en la otra ecuación. Lo importante aquí es que siempre sustituyes valores que son equivalentes.

 

Por ejemplo:

 

Sean es 5 años mayor que cuatro veces la edad de su hija. Su hija tiene 7 años. ¿Cuántos años tiene Sean?

 

Podrías resolver este problema con la mente. La hija de Sean tiene 7 años, entonces “cuatro veces la edad de su hija” es 28, y si sumamos 5 años nos da 33. Sean tiene 33 años.

 

Si resolviste el problema de esa forma, hiciste una sustitución simple — sustituiste el valor “7” de “la edad de su hija.” Y supiste en la segunda parte del problema que “su hija tiene 7 años.” Entonces sustituiste el valor de “7” por “la edad de su hija” en la primera parte del problema porque sabías que estas dos cantidades son iguales.

 

Veamos otro ejemplo simple de ecuaciones que pueden resolverse con sustitución.

 

 

 

 

Puedes sustituir un valor por una variable incluso si es una expresión. Aquí hay un ejemplo.

 

 

 

 

Recuerda, una solución de un sistema de ecuaciones debe ser la solución para cada una de las ecuaciones en el sistema. El par ordenado (4, −1) funciona para ambas ecuaciones, por lo que sabes que es una solución del sistema.

 

Veamos otro ejemplo cuya sustitución incluye la propiedad distributiva.

 

 

 

 

En los ejemplos anteriores, una de las ecuaciones ya estaba dada en términos de la variable x y y. Esto nos permitió sustituir rápidamente el valor en la otra ecuación y resolver una de las incógnitas.

 

Algunas veces primero tendrás que reescribir una de las ecuaciones en términos de una de las variables antes de que puedas sustituir. Observa el ejemplo siguiente.

 

 

 

 

Resuelve el sistema para x y y. 2y = x + 8 2y − 10 = 2x   A) x = −3, y = 2   B) x = −2, y = 3   C) x = −5, y = 2   D) x = 0, y = -5   Mostrar/Ocultar Respuesta A) x = −3, y = 2 Incorrecto. Si sustituyes los valores x = −3 y y = 2 en la primera ecuación, obtienes el enunciado inválido: 2(2) = −3 + 9. Para resolver este sistema, intenta reescribiendo la primera ecuación como x = 2y − 8. Luego sustituye 2y − 8 por x en la segunda ecuación y resuelve y. La respuesta correcta es x = −2, y = 3.   B) x = −2, y = 3 Correcto. Si sustituyes estos valores en cualquiera de las ecuaciones obtienes el enunciado válido: 2(3) = −2 + 8, y 2(3) − 10 = 2(−2).   C) x = −5, y = 2 Incorrecto. Si sustituyes los valores x = −5 y y = 2 en la segunda ecuación, obtienes el enunciado inválido: 2(2) − 10 = 2. Para resolver este sistema, intenta reescribiendo la primera ecuación como x = 2y − 8. Luego sustituye 2y − 8 por x en la segunda ecuación y resuelve y. La respuesta correcta es x = −2, y = 3.   D) x = 0, y = -5 Incorrecto. Si sustituyes los valores x = 0 y y = −5 en la segunda ecuación, obtienes el enunciado inválido: 2(−5) − 10 = 2(0). Para resolver este sistema, intenta reescribiendo la primera ecuación como x = 2y − 8. Luego sustituye 2y − 8 por x en la segunda ecuación y resuelve y. La respuesta correcta es x = −2, y = 3.

 

 

Hay algunos casos donde usar el método de sustitución dará resultados que, a primera vista, no tienen sentido. Veamos algunos de estos casos y estudiemos lo que está pasando.

 

 

 

 

Obtienes el enunciado falso −8 = 4. ¿Qué significa? La gráfica de este sistema nos da una pista de lo que está pasando.

 

 

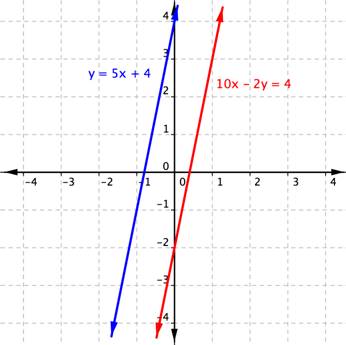
Las rectas son paralelas, nunca se intersectan y no hay solución para este sistema de ecuaciones lineales. Observa que el resultado −8 = 4 no es una solución. Es simplemente un enunciado inválido e indica que no hay solución.

 

Ahora veamos este problema, que también es interesante.

 

Resolver x y y.

y = −0.5x

9y = −4.5x

 

Sustituyendo −0.5x por y en la segunda ecuación, encuentras lo siguiente:

 

 

Esta ves obtienes un enunciado válido: −4.5x = −4.5x. Pero ¿qué significa este tipo de resultado? Una vez más, graficamos para ayudarnos a entender este sistema.

 

 

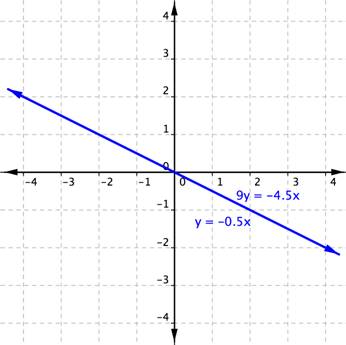
Este sistema consiste en dos ecuaciones que representan la misma recta; las rectas son colineales. Cada punto en la recta será una solución del sistema y es por eso que el método de sustitución resultó en un enunciado válido. En este caso, hay un número infinito de soluciones.

 

 

Aubrey está usando el método de sustitución para resolver el siguiente sistema de ecuaciones:   y − x = 21 2y = 2x + 16   Llega a la solución 8 = 21. Ella piensa que el resultado significa que las rectas son paralelas y que el sistema no tiene solución.   Aubrey quiere comprobar su respuesta. ¿Cuál de las siguientes acciones la ayudará mejor a corroborar que las dos ecuaciones del sistema son, de hecho, paralelas?   A) Comprobar si las pendientes de ambas rectas son iguales, y las intersecciones en y son distintas.   B) Comprobar si alguna de las rectas pasa por el origen.   C) Comprobar si las rectas tienen la misma intersección en y.   D) Comprobar si ambas rectas pasan por el punto (8, 21).   Mostrar/Ocultar Respuesta A) Comprobar si las pendientes de ambas rectas son iguales, y las intersecciones en y son distintas. Correcto. Las rectas paralelas tienen la misma pendiente, pero también debe comprobar que tienen distintas intersecciones en y porque las rectas podrían ser colineales (recuerda que dos rectas colineales son la misma recta). Si Aubrey encuentra que las pendientes de las rectas son las mismas y que las intersecciones en y son distintas, entonces puede estar segura de que su respuesta es correcta.   B) Comprobar si alguna de las rectas pasa por el origen. Incorrecto. El origen no tiene nada que ver con saber si dos rectas son paralelas. En el caso de este sistema, ninguna de las rectas pasa por el origen, pero las rectas son paralelas. Si Aubrey encuentra que las pendientes de las rectas son las mismas y que las intersecciones en y son distintas, entonces puede estar segura de que su respuesta es correcta.   C) Comprobar si las rectas tienen la misma intersección en y. Incorrecto. Es cierto que las rectas con la misma intersección en y nunca son paralelas, porque las rectas paralelas no se intersectan. Pero sólo comprobar que las intersecciones en y no son la misma no es suficiente. Para ser paralelas, las rectas también deben tener la misma pendiente. Si Aubrey encuentra que las pendientes de las rectas son las mismas y que las intersecciones en y son distintas, entonces puede estar segura de que su respuesta es correcta.   D) Comprobar si ambas rectas pasan por el punto (8, 21). Incorrecto. Si bien ella llegó a la respuesta 8 = 21, esto no significa que las rectas se intersectan en el punto (8, 21). Si Aubrey encuentra que las pendientes de las rectas son las mismas y que las intersecciones en y son distintas, entonces puede estar segura de que su respuesta es correcta.

 

 

Los sistemas de ecuaciones son herramientas muy útiles para modelar situaciones reales y contestar preguntas sobre ellas. Si puedes traducir la aplicación a dos ecuaciones lineales con dos variables, entonces tienes un sistema de ecuaciones que puedes resolver para encontrar la solución. Puedes usar cualquier método para resolver el sistema de ecuaciones. Usa el método de sustitución en este ejemplo.

 

Con el objetivo de vender más producto, una granja local vende costales de manzanas de dos tamaños: mediano y grande. Un costal mediano contiene 4 manzanas Macintosh y 1 manzana Granny Smith y cuesta $2.80. Un costal grande contiene 8 manzanas Macintosh y 4 manzanas Granny Smith y cuesta $7.20. El precio de una manzana Granny Smith es el mismo en el costal mediano que en el costal grande. El precio de una manzana Macintosh es el mismo en el costal mediano que en el costal grande. ¿Cuál es el precio de cada tipo de manzana?

 

Empecemos creando un sistema de ecuaciones que represente lo que está sucediendo en el problema. Hay dos tipos de manzanas y dos tipos de costales. Sea m el costo de una manzana Macintosh y g el costo de una manzana Granny Smith. Hagamos una tabla para ver lo que sabemos.

 

 

Ahora que tienes dos ecuaciones con la misma variable puedes resolver el sistema. Usarás sustitución. Los pasos se muestran en el ejemplo siguiente:

 

 

 

 

Usar el método de sustitución puede ser una estrategia efectiva para resolver problemas geométricos.

 

 

 

 

El método de sustitución es una manera de resolver sistemas de ecuaciones. Para usar el método de sustitución, toma una ecuación y encuentra una expresión para una de las variables en términos de la otra variable. Luego sustituye esa expresión por la variable en la segunda ecuación. Puedes entonces resolver esta ecuación como si ahora tuviera una variable. Resolver ecuaciones usando el método de sustitución nos da tres resultados posibles: un valor para cada variable en el sistema (indicando una solución), un enunciado inválido (indicando que no hay soluciones), o un enunciado válido (indicando un número infinito de soluciones).