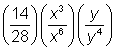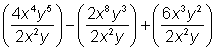Operaciones con Polinomios

 

Objetivos de Aprendizaje

·         Sumar polinomios con más de una variable.

·         Restar polinomios con más de una variable.

·         Multiplicar polinomios con más de una variable.

·         Dividir polinomios con más de una variable.

 

 

Así como puedes realizar las cuatro operaciones en polinomios con una variable, puedes sumar, restar, multiplicar, y dividir polinomios con más de una variable. El proceso es exactamente el mismo, pero tienes más variables que tomar en cuenta. Cuando estás sumando o restando polinomios con más de una variable, debes tener cuidado de combinar sólo los términos semejantes. Cuando multiplicas o divides, también debes poner atención a todas las variables y términos. Puedes multiplicar y dividir términos que no son semejantes, pero al sumar o restar términos, deben ser semejantes.

 

 

Para sumar polinomios, primero necesitas identificar los términos semejantes en los polinomios y luego combinarlos de acuerdo con operaciones correctas. Como los términos semejantes deben tener exactamente las mismas variables elevadas a la misma potencia, hay que poner atención al identificarlos en los polinomios de múltiples variables. Algunas veces se usan paréntesis para distinguir entre la suma de dos polinomios y la suma de una colección de monomios. En el caso de la suma, puedes simplemente eliminar los paréntesis y realizar la suma.

 

 

 

 

A algunas personas se les hace más fácil escribir una suma polinomial de manera vertical para combinar los términos semejantes. El proceso de sumar polinomios es el mismo, pero el arreglo de los términos es diferente. El ejemplo siguiente muestra este método “vertical” de sumar polinomio:

 

 

 

 

Cuando no hay un término semejante para cada polinomio, habrá espacios vacíos en el arreglo vertical de los polinomios. Este arreglo hace más fácil comprobar que estas combinado sólo términos semejantes.

 

 

 

 

Suma. (8a3b2 + 6a2b – 4b2 + 5) + (10a2b – 4a3b2 + 6a2 – 7)   A) 18a3b2 + 2a2b + 2b2 – 2   B) 4a3b2 + 16a2b + 6a2 – 4b2 – 2   C) 18a3b2 + 2a2b + 6a2 – 4b2 – 2   D) 4a6b4 + 16a4b2 + 6a2 – 4b2 – 2   Mostrar/Ocultar Respuesta A) 18a3b2 + 2a2b + 2b2 – 2 Incorrecto. Asegúrate de sólo combinar los términos semejantes. La secuencia de términos en los polinomios no es la misma. Además, los ´terminos −4b2 y 6a2 no son términos semejantes y no pueden ser combinados. La respuesta correcta es 4a3b2 + 16a2b + 6a2 – 4b2 – 2.   B) 4a3b2 + 16a2b + 6a2 – 4b2 – 2 Correcto. (8a3b2 + 6a2b – 4b2 + 5) + (10a2b – 4a3b2 + 6a2 – 7)   = 8a3b2 – 4a3b2 + 6a2b + 10a2b – 4b2 + 6a2 – 7+ 5   = 4a3b2 + 16a2b + 6a2 – 4b2 – 2.   C) 18a3b2 + 2a2b + 6a2 – 4b2 – 2 Incorrecto. Asegúrate de sólo combinar los términos semejantes. La secuencia de términos en los polinomios no es la misma. La respuesta correcta es 4a3b2 + 16a2b + 6a2 – 4b2 – 2.   D) 4a6b4 + 16a4b2 + 6a2 – 4b2 – 2 Incorrecto. Cuando sumes términos semejantes, no sumes los exponentes, sólo los coeficientes. La respuesta correcta es 4a3b2 + 16a2b + 6a2 – 4b2 – 2.

 

 

 

Para restar polinomios con más de una variable, puedes aplicar el mismo proceso usado para restar polinomios con una variable. Para eliminar los paréntesis después del signo de resta, debes multiplicar cada término por −1.

 

 

 

 

Una manera alternativa de resolverlo es el método vertical para arreglar el problema de resta. Este método se muestra a continuación para un problema distinto. Ambos métodos son efectivos para restar polinomios — la idea es identificar y organizar los términos semejantes para poder operarlos.

 

 

 

Los ejemplos siguientes ilustran los métodos de izquierda a derecha y vertical para ella misma resta de polinomios. Piensa en qué método te parece más fácil.

 

 

 

 

 

 

 

Los polinomios con más de una variable también pueden multiplicarse unos con otros. Usas las mismas técnicas que cuando multiplicas polinomios con una variable. Considera el siguiente ejemplo.

 

(4x²y³)(5x⁴y²)

 

Ese es un ejemplo de una multiplicación de dos polinomios, específicamente monomios, con dos variables. Para hacer esta multiplicación, multiplica los coeficientes y usas las reglas de los exponentes para encontrar el exponente para cada variable y calcular el producto. Veamos.

 

(4x²y³)(5x⁴y²) = (4 • 5)(x²⁺⁴)(y³⁺²) = 20x⁶y⁵

 

Para multiplicar uno monomio por un binomio, usas la propiedad distributiva de la misma forma que cuando multiplicas polinomios de una variable.

 

 

 

 

Para multiplicar dos binomios que contienen más de una variable, puedes usar el método FOIL (First, Outer, Inner, Last) que funciona para binomios de una variable. Después de todo, FOIL es simplemente un atajo para usar la propiedad distributiva para multiplicar cada término en un binomio por cada término en el otro binomio. Este proceso funciona para multiplicar cualquier par de binomios. A continuación se muestran dos ejemplos.

 

 

 

 

El siguiente ejemplo muestra el producto de un binomio y un trinomio, cada uno con dos variables. Como FOIL sólo puede usarse con el producto de dos binomios, necesitas multiplicar sistemáticamente cada término en el binomio con cada término en el trinomio.

 

 

 

 

Al multiplicar polinomios multivariable de esta manera, algunas personas prefieren acomodar la multiplicación de manera vertical — como lo harías al multiplicar 45 • 189. El ejemplo siguiente muestra (9b – ab)(5a²b + 7ab – b) acomodado de manera vertical.

 

 

 

 

Observa que los productos de los dos ejemplos son iguales, aunque el orden individual de los términos es diferente debido a los métodos diferentes de solución.

 

 

Encuentra el producto. −4pt2(5pt3 + 3pt2 – t)   A) −20p2t5 – 12p2t4 + 4pt3   B) −20t5 + 12p2t4 – 4pt3   C) −20pt6 – 12pt4 + 4pt2   D) −20p2t5 + 3pt2 – t   Mostrar/Ocultar Respuesta A) −20p2t5 – 12p2t4 + 4pt3 Correcto. Al reescribir la resta como una suma de opuestos obtienes −4pt2(5pt3 + 3pt2 + (−t)). Distribuyendo el monomio −4pt2 obtienes −4pt2 • 5pt3 + (−4pt2 • 3pt2) + (−4pt2 • −t), que es −20p2t5 – 12p2t4 + 4pt3.   B) −20t5 + 12p2t4 – 4pt3 Incorrecto. El negativo debe ser distribuido a todos los términos con el 4pt2. Esto cambia el signo de los términos de en medio y el último. La respuesta correcta es −20p2t5 – 12p2t4 + 4pt3.   C) −20pt6 – 12pt4 + 4pt2 Incorrecto. Por las leyes de los exponentes, sumas (no multiplicas) los exponentes cuando estas multiplicando: −4pt2 • 5pt3 + (−4pt2 • 3pt2) + (−4pt2 • −t) es −20p2t5 – 12p2t4 + 4pt3.La respuesta correcta es −20p2t5 – 12p2t4 + 4pt3.   D) −20p2t5 + 3pt2 – t Incorrecto. Debes distribuir el monomio a los tres términos en el polinomio, no sólo al primero: −4pt2 • 5pt3 + (−4pt2 • 3pt2) + (−4pt2 • −t). La respuesta correcta es −20p2t5 – 12p2t4 + 4pt3.

 

 

 

La cuarta operación aritmética es la división. Los polinomios con más de una variable también pueden dividirse. Cuando divides monomios con más de una variable, divides los coeficientes y luego divides las variables. Cuando hay exponentes con la misma base, las reglas de los exponentes dicen que puedes dividir al restar los exponentes. Considera el siguiente ejemplo.

 

 

Ahora vemos otro ejemplo de dividir un trinomio con más de una variable entre un monomio con más de una variable. Se sigue el mismo procedimiento que cuando tenías una variable, pero necesitas poner atención al distinguir entre variables.

 

 

 

 

 

Dividir.   A) 5st2 – 2s2t + 1   B) 5st2 – 10s3t3 + 5st2   C) 20st2 – 5s2t   D)   Mostrar/Ocultar Respuesta A) 5st2 – 2s2t + 1 Correcto. Divide cada término en el polinomio entre el monomio: .   B) 5st2 – 10s3t3 + 5st2 Incorrecto. Sólo dividiste el primer término. Divide cada término en el polinomio entre el monomio: . La respuesta correcta es 5st2 – 2s2t + 1.   C) 20st2 – 5s2t Incorrecto. Debes dividir, no restar, los coeficientes. La respuesta correcta es 5st2 – 2s2t + 1.   D) Incorrecto. Realiza la división para simplificar. No hay problema con que no sean términos semejantes, de todos modos puedes dividir. Debes tener términos semejantes cuando sumas o restas términos, no cuando multiplicas o divides. Divide cada término en el polinomio entre el monomio: . La respuesta correcta es 5st2 – 2s2t + 1.

 

 

 

Al realizar sumas, restas, multiplicaciones , y divisiones de polinomios con más de una variable se siguen los mismos pasos que al operar polinomios de una variable. Las cosas importantes en las que hay que poner atención son que debes combinar sólo términos semejantes, aplicar correctamente las reglas de los exponentes, las operaciones con enteros, y el orden de las operaciones.