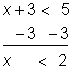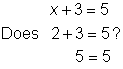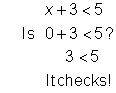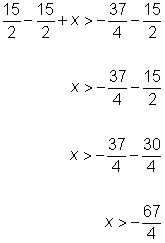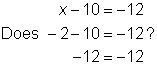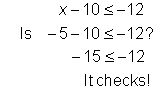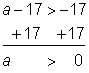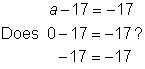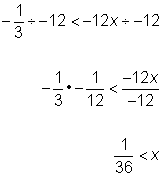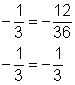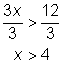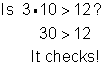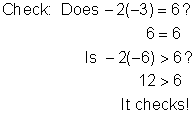Solving One-Step Inequalities
Learning Objective(s)
· Represent inequalities on a number line.
· Use the addition property of inequality to isolate variables and solve algebraic inequalities, and express their solutions graphically.
· Use the multiplication property of inequality to isolate variables and solve algebraic inequalities, and express their solutions graphically.
Introduction
Sometimes there is a range of possible values to describe a situation. When you see a sign that says “Speed Limit 25,” you know that it doesn’t mean that you have to drive exactly at a speed of 25 miles per hour (mph). This sign means that you are not supposed to go faster than 25 mph, but there are many legal speeds you could drive, such as 22 mph, 24.5 mph or 19 mph. In a situation like this, which has more than one acceptable value, inequalities are used to represent the situation rather than equations.
What is an Inequality?
An inequality is a mathematical statement that compares two expressions using an inequality sign. In an inequality, one expression of the inequality can be greater or less than the other expression. Special symbols are used in these statements. The box below shows the symbol, meaning, and an example for each inequality sign.
|
Inequality Signs
x Example: The number of days in a week is not equal to 9.
x > y x is greater than y. Example: 6 > 3 Example: The number of days in a month is greater than the number of days in a week.
x < y x is less than y. Example: The number of days in a week is less than the number of days in a year.
Example: 31 is greater than or equal to the number of days in a month.
Example: The speed of a car driving legally in a 25 mph zone is less than or equal to 25 mph.
|
The important thing about inequalities is that there can be multiple solutions. For example, the inequality “31 ≥ the number of days in a month” is a true statement for every month of the year—no month has more than 31 days. It holds true for January, which has 31 days (31 ≥ 31); September, which has 30 days (31 ≥ 30); and February, which has either 28 or 29 days depending upon the year (31 ≥ 28 and 31 ≥ 29).
The inequality x > y can also be written as y < x. The sides of any inequality can be switched as long as the inequality symbol between them is also reversed.
Inequalities can be graphed on a number line. Below are three examples of inequalities and their graphs.
x < 2
![]()
x ≤ −4
![]()
x ³ −3
![]()
Each of these graphs begins with a circle—either an open or closed (shaded) circle. This point is often called the end point of the solution. A closed, or shaded, circle is used to represent the inequalities greater than or equal to (![]() ) or less than or equal to (
) or less than or equal to (![]() ). The point is part of the solution. An open circle is used for greater than (>) or less than (<). The point is not part of the solution.
). The point is part of the solution. An open circle is used for greater than (>) or less than (<). The point is not part of the solution.
The graph then extends endlessly in one direction. This is shown by a line with an arrow at the end. For example, notice that for the graph of ![]() shown above, the end point is −3, represented with a closed circle since the inequality is greater than or equal to −3. The blue line is drawn to the right on the number line because the values in this area are greater than −3. The arrow at the end indicates that the solutions continue infinitely.
shown above, the end point is −3, represented with a closed circle since the inequality is greater than or equal to −3. The blue line is drawn to the right on the number line because the values in this area are greater than −3. The arrow at the end indicates that the solutions continue infinitely.
You can solve most inequalities using the same methods as those for solving equations. Inverse operations can be used to solve inequalities. This is because when you add or subtract the same value from both sides of an inequality, you have maintained the inequality. These properties are outlined in the blue box below.
|
Addition and Subtraction Properties of Inequality If a > b, then a + c > b + c If a > b, then a − c > b − c
|
Because inequalities have multiple possible solutions, representing the solutions graphically provides a helpful visual of the situation. The example below shows the steps to solve and graph an inequality.
| Example | |||
| Problem | Solve for x.
|
| |
|
| Isolate the variable by subtracting 3 from both sides of the inequality. | ||
| Answer | x < 2 |
| |
The graph of the inequality x < 2 is shown below.
![]()
Just as you can check the solution to an equation, you can check a solution to an inequality. First, you check the end point by substituting it in the related equation. Then you check to see if the inequality is correct by substituting any other solution to see if it is one of the solutions. Because there are multiple solutions, it is a good practice to check more than one of the possible solutions. This can also help you check that your graph is correct.
The example below shows how you could check that x < 2 is the solution to x + 3 < 5.
| Example | ||||
| Problem | Check that x < 2 is the solution to x + 3 < 5. |
| ||
|
| Substitute the end point 2 into the related equation, x + 3 = 5. | |||
|
| Pick a value less than 2, such as 0, to check into the inequality. (This value will be on the shaded part of the graph.) | |||
| Answer | x < 2 is the solution to x + 3 < 5. |
| ||
The following examples show additional inequality problems. The graph of the solution to the inequality is also shown. Remember to check the solution. This is a good habit to build!
| Advanced Example | |||
| Problem | Solve for x.
|
| |
|
| Subtract | ||
| Answer |
|
| |
| Example | |||
| Problem | Solve for x.
|
| |
|
| Isolate the variable by adding 10 to both sides of the inequality. | ||
| Answer | x |
| |
The graph of this solution in shown below. Notice that a closed circle is used because the inequality is “less than or equal to” (![]() ). The blue arrow is drawn to the left of the point −2 because these are the values that are less than −2.
). The blue arrow is drawn to the left of the point −2 because these are the values that are less than −2.
![]()
| Example | |||||
| Problem | Check that |
| |||
|
|
| Substitute the end point −2 into the related equation x – 10 = −12. | |||
|
|
| Pick a value less than −2, such as −5, to check in the inequality. (This value will be on the shaded part of the graph.) | |||
| Answer |
|
| |||
| Example | |||
| Problem | Solve for a.
|
| |
|
| Isolate the variable by adding 17 to both sides of the inequality. | ||
| Answer |
|
| |
The graph of this solution in shown below. Notice that an open circle is used because the inequality is “greater than” (>). The arrow is drawn to the right of 0 because these are the values that are greater than 0.
![]()
| Example | |||
| Problem | Check that | ||
|
| Substitute the end point, 0 into the related equation. | ||
|
| Pick a value greater than 0, such as 20, to check in the inequality. (This value will be on the shaded part of the graph.) | ||
| Answer |
|
| |
| Advanced Question Solve for x:
A) x ≤ 0 B) x > 35 C) x ≤ 7 D) x ≥ 5
|
Solving an inequality with a variable that has a coefficient other than 1 usually involves multiplication or division. The steps are like solving one-step equations involving multiplication or division EXCEPT for the inequality sign. Let’s look at what happens to the inequality when you multiply or divide each side by the same number.
| Let’s start with the true statement: | 10 > 5 |
| Let’s try again by starting with the same true statement: | 10 > 5 |
| Next, multiply both sides by the same positive number: | 10 • 2 > 5 • 2 | This time, multiply both sides by the same negative number: | 10 • −2 > 5 • −2 | |
| 20 is greater than 10, so you still have a true inequality: | 20 > 10 | Wait a minute! −20 is not greater than −10, so you have an untrue statement. | −20 > −10 | |
| When you multiply by a positive number, leave the inequality sign as it is! |
| You must “reverse” the inequality sign to make the statement true: | −20 < −10 |
When you multiply by a negative number, “reverse” the inequality sign.
Whenever you multiply or divide both sides of an inequality by a negative number, the inequality sign must be reversed in order to keep a true statement.
These rules are summarized in the box below.
|
Multiplication and Division Properties of Inequality
If a > b, then ac > bc, if c > 0 If a > b, then ac < bc, if c < 0
If a > b, then If a > b, then
|
Keep in mind that you only change the sign when you are multiplying and dividing by a negative number. If you add or subtract a negative number, the inequality stays the same.
| Advanced Example | |||
| Problem | Solve for x.
|
| |
|
| Divide both sides by -12 to isolate the variable. Since you are dividing by a negative number, you need to change the direction of the inequality sign. | ||
|
Check | Does
Is
It checks! | Check your solution by first checking the end point
Pick a value greater than | |
| Answer |
|
| |
| Example | |||
| Problem | Solve for x. 3x > 12 |
| |
|
|
| Divide both sides by 3 to isolate the variable. | |
|
|
| Check your solution by first checking the end point 4, and then checking another solution for the inequality. | |
| Answer |
|
| |
The graph of this solution is shown below.
![]()
There was no need to make any changes to the inequality sign because both sides of the inequality were divided by positive 3. In the next example, there is division by a negative number, so there is an additional step in the solution!
| Example | ||||
| Problem | Solve for x. −2x > 6 |
| ||
|
|
| Divide each side of the inequality by −2 to isolate the variable, and change the direction of the inequality sign because of the division by a negative number. | ||
|
|
|
| ||
|
| Check your solution by first checking the end point −3, and then checking another solution for the inequality. | |||
| Answer |
|
| ||
Because both sides of the inequality were divided by a negative number, −2, the inequality symbol was switched from > to <. The graph of this solution is shown below.
![]()
| Solve for y: −10y ≥ 150
A) y = −15 B) y ≥ −15 C) y ≤ −15 D) y ≥ 15
|
| Advanced Question Solve for a:
A) B) C) D)
|
Summary
Solving inequalities is very similar to solving equations, except you have to reverse the inequality symbols when you multiply or divide both sides of an inequality by a negative number. Since inequalities can have multiple solutions, it is customary to represent the solution to an inequality graphically as well as algebraically. Because there is usually more than one solution to an inequality, when you check your answer you should check the end point and one other value to check the direction of the inequality.