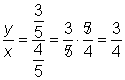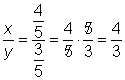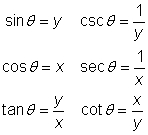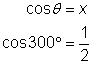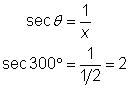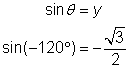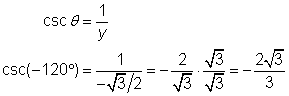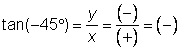El Círculo Unidad en Trigonometría
Objetivos de Aprendizaje
· Entender el círculo unidad, ángulo de referencia, lado terminal, posición estándar.
· Encontrar los valores exactos de la función trigonométrica para ángulos que miden 30°, 45°, y 60° usando el círculo unidad.
· Encontrar los valores exactos de la función trigonométrica para cualquier ángulo cuyo ángulo de referencia mida 30°, 45°, o 60°.
· Determinar los cuadrantes donde el seno, coseno, y tangente son positivos y negativos.
Introducción
Los matemáticos crean definiciones porque tienen una utilidad para resolver ciertos tipos de problemas. Por ejemplo, las seis funciones trigonométricas se definieron originalmente en términos de triángulos rectángulos porque eran útiles para resolver problemas del mundo real que involucran triángulos rectángulos, como por ejemplo encontrar ángulos de elevación. El dominio, o conjunto de valores de entrada, de estas funciones es el conjunto de ángulos entre 0° y 90°. Ahora aprenderás nuevas definiciones para estas funciones en las que el dominio es el conjunto de todos los ángulos. Las nuevas funciones tendrán los mismos valores que las funciones originales cuando la entrada sea un ángulo agudo. En un triángulo rectángulo sólo puedes tener ángulos agudos, pero verás que la definición se extiende para incluir otros ángulos.
Un uso de estas nuevas funciones es que pueden ser utilizadas para encontrar los lados y medidas de ángulos desconocidos en cualquier triángulo. Estas nuevas funciones pueden usarse en muchas situaciones que no tienen nada que ver con triángulos.
Antes de ver las nuevas definiciones, necesitas familiarizarte con la manera estándar que usan los matemáticos para dibujar y nombrar ángulos.
En geometría, sabes que un ángulo está formado por dos rayos. Los rayos se unen en un punto llamado vértice.
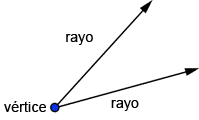
En trigonometría, los ángulos se posicionan en ejes de coordenadas. El vértice siempre se coloca en el origen y uno de los rayos siempre se coloca en el eje-x positivo. Este rayo se llama lado inicial del ángulo. El otro rayo se llama lado terminal del ángulo. A este posicionamiento del ángulo se llama posición estándar. La letra Griega teta (![]() ) se usa normalmente para representar una medida de un ángulo. A continuación se muestran dos ángulos en la posición estándar.
) se usa normalmente para representar una medida de un ángulo. A continuación se muestran dos ángulos en la posición estándar.
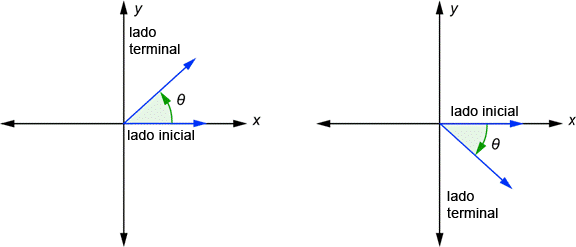
Cuando se dibuja un ángulo en la posición estándar, no tiene dirección. En el dibujo anterior, observa que hay flechas curvas pequeñas. La de la izquierda va en contra de las manecillas del reloj y se define como un ángulo positivo. La de la derecha va a favor de las manecillas del reloj y se define como un ángulo negativo. Si usas un transportador para medir los ángulos, tendrás que miden 50° en ambos casos. Nos referimos al primero como un ángulo de 50°, y al secundo como un ángulo de ![]() .
.
¿Por qué es necesario tener ángulos negativos? Al igual que todas las definiciones, es una cuestión de conveniencia. Una nave espacial en una órbita circular alrededor del ecuador de la Tierra podría estar viajando en cualquiera de las dos direcciones. Entonces podrías decir que viaja en un ángulo de ![]() para indicar que va en la dirección opuesta que otra nave que viaja en un ángulo de 50°. ¿Por qué ir en contra de las manecillas del reloj es positivo? Es simplemente una convención — algo en lo que los matemáticos se han puesto de acuerdo — porque una dirección debe ser positiva y la otra debe ser negativa.
para indicar que va en la dirección opuesta que otra nave que viaja en un ángulo de 50°. ¿Por qué ir en contra de las manecillas del reloj es positivo? Es simplemente una convención — algo en lo que los matemáticos se han puesto de acuerdo — porque una dirección debe ser positiva y la otra debe ser negativa.
Par ver cómo ángulos positivos resultan de una rotación en contra de las manecillas del reloj, y ángulos negativos de una rotación a favor de las manecillas del reloj, intenta con el ejercicio interactivo siguiente. Ya sea que introduzcas una medida de un ángulo en el campo llamado “Ángulo” y presionas enter o usas el control deslizante para mover el lado terminal de ángulo θ pasando por los cuadrantes.
| Ejemplo | |
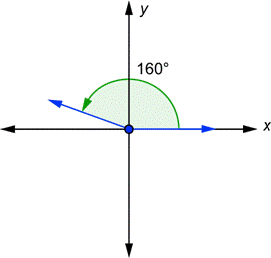
| Problema | Dibujar un ángulo de 160° en la posición estándar. |
|
| El ángulo es positivo, por lo que empiezas en el eje-x y vas hasta 160° a favor de las manecillas del reloj. |
| Respuesta |
|
| Ejemplo | |
| Problema | Dibujar un ángulo de |
|
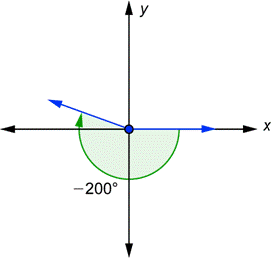
| El ángulo es negativo, por lo que empiezas en el eje-x y vas hasta 200° en contra de las manecillas del reloj. Recuerda que 180° es una línea recta. Eso significa que llegarás al eje-x negativo, y lo pasarás otros 20°. |
| Respuesta |
|
Observa que los lados terminales en los dos ejemplos anteriores son el mismo, pero representan ángulos distintos. A esos pares de ángulos se les llama ángulos coterminales.
Para cada ángulo dibujado en la posición estándar, existe un ángulo relacionado conocido como ángulo de referencia. Este es el ángulo formado por el lado terminal y el eje-x. El ángulo de referencia siempre se considera positivo, y tiene un valor entre 0° y 90°. A continuación se muestran dos ángulos en la posición estándar.
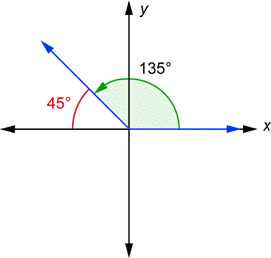
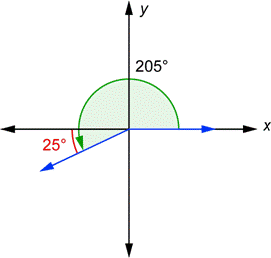
Puedes ver que el lado terminal del ángulo 135° y el eje-x forman un ángulo de 45° grados (esto es porque los dos ángulos deben sumar 180°). El ángulo de 45° mostrado en rojo, es el ángulo de referencia para 135°. El lado terminal del ángulo de 205° y el eje-x forman un ángulo de 25°. Es de 25° porque ![]() . Este ángulo de 25°, mostrado en rojo, es el ángulo de referencia para 205°.
. Este ángulo de 25°, mostrado en rojo, es el ángulo de referencia para 205°.
Aquí hay otros dos ángulos en la posición estándar.
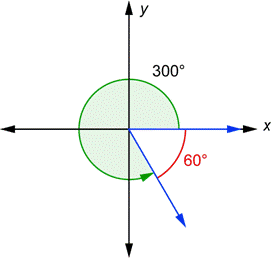
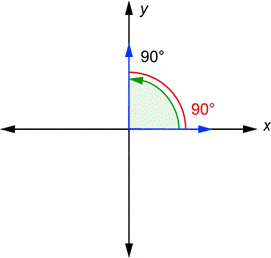
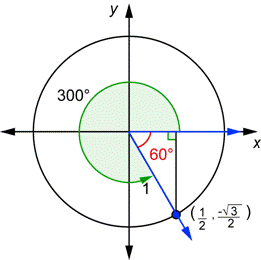
El lado terminal del ángulo de 300° y el eje-x forman un ángulo de 60° (esto es porque los dos ángulos deben sumar 360°). Este ángulo de 60°, mostrado en rojo, es el ángulo de referencia para el ángulo de 300°. El lado terminal del ángulo de 90° y el eje-x forman un ángulo de 90°. El ángulo de referencia es el mismo que el ángulo original. De hecho, cualquier ángulo entre 0° y 90° es igual a su ángulo de referencia.
| Ejemplo | ||
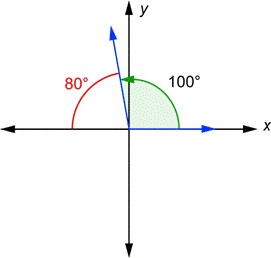
| Problema | ¿Cuál es el ángulo de referencia para 100°? | |
|
|
| El lado terminal está en el Cuadrante II. El ángulo original y el ángulo de referencia forman juntos una línea recta por el eje-x, por lo que su suma es 180°. Entonces el ángulo de referencia es 80°. |
| Respuesta | El ángulo de referencia para 100° es 80°. |
|
| Ejemplo | ||
| Problema | ¿Cuál es el ángulo de referencia para | |
|
|
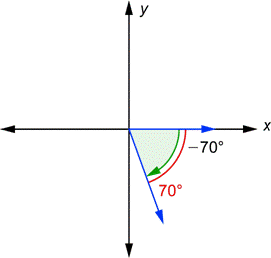
| El lado terminal y el eje-x forman el “mismo” ángulo que el original. Un ángulo de referencia siempre es un número positivo, por lo que el ángulo de referencia aquí es 70°, mostrado en rojo. |
| Respuesta | El ángulo de referencia para |
|
| ¿Cuál es el ángulo de referencia para 310°?
A) 40° B) 50° C) D)
|
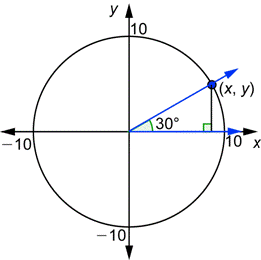
Un círculo unidad es un círculo con centro en el origen y con radio igual a 1, como se muestra abajo.
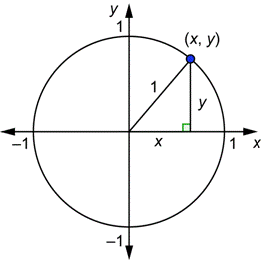
Si ![]() son las coordenadas de un punto en el círculo, entonces puedes ver del triángulo rectángulo en el dibujo y del Teorema de Pitágoras que
son las coordenadas de un punto en el círculo, entonces puedes ver del triángulo rectángulo en el dibujo y del Teorema de Pitágoras que ![]() . Esta es la ecuación de un círculo unidad.
. Esta es la ecuación de un círculo unidad.
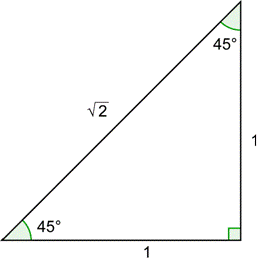
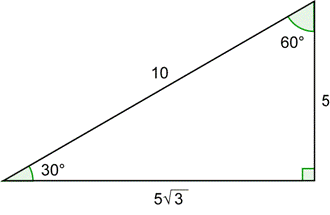
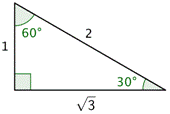
El triángulo 30° - 60° - 90° se muestra abajo a la izquierda. Junto a él hay un ángulo de 30° dibujado en la posición estándar junto con un círculo unidad.
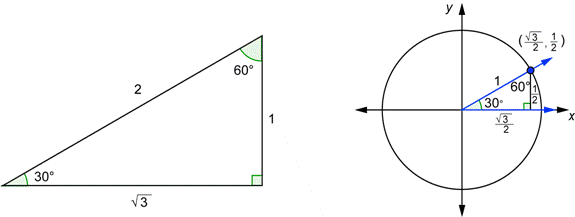
Los dos triángulos tienen los mismos ángulos, por lo que son similares. Entonces, los lados correspondientes son proporcionales. La hipotenusa en el de la derecha tiene longitud 1 (porque es un radio). Como ésta es la mitad de la hipotenusa en el de la izquierda, todos los lados en el de la derecha son la mitad de los lados correspondientes en el de la izquierda. Por ejemplo, el lado adyacente al ángulo de 30° a la izquierda es ![]() ; entonces el lado correspondiente en el triángulo de la derecha tiene la mitad de eso, o
; entonces el lado correspondiente en el triángulo de la derecha tiene la mitad de eso, o ![]() .
.
Observa el triángulo rectángulo a la izquierda. Usando las definiciones de seno y coseno:
![]()
Ahora observa el punto donde el lado terminal intersecta el círculo unidad. La coordenada-x es igual a ![]() , y la coordenada-y es igual a
, y la coordenada-y es igual a ![]() . Esto no es una coincidencia. Veamos un caso más general.
. Esto no es una coincidencia. Veamos un caso más general.
Supongamos que dibujas cualquier ángulo agudo ![]() en la posición estándar junto con un círculo unidad, como se muestra abajo.
en la posición estándar junto con un círculo unidad, como se muestra abajo.
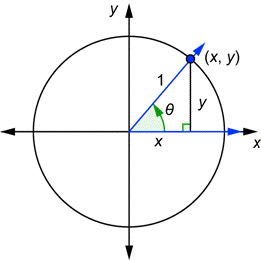
El lado terminal del ángulo intersecta al círculo unidad en el punto ![]() . Escribamos las definiciones de las seis funciones trigonométricas y luego las reescribimos refiriéndonos al triángulo anterior y usando las variables x y y.
. Escribamos las definiciones de las seis funciones trigonométricas y luego las reescribimos refiriéndonos al triángulo anterior y usando las variables x y y.
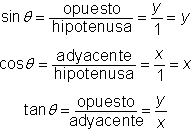
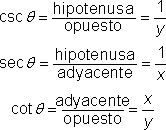
La primera ecuación y la que está debajo de ella, te dice:
![]()
Ahora puedes ver que la coordenada-y de este punto siempre es igual al seno del ángulo, y la coordenada-x de este punto siempre es igual al coseno del ángulo.
Ahora considera cualquier ángulo ![]() en la posición estándar junto con un círculo unidad. El lado terminal intersecta el círculo en algún punto
en la posición estándar junto con un círculo unidad. El lado terminal intersecta el círculo en algún punto ![]() . Dependiendo del ángulo, ese punto puede quedar en el primero, segundo, tercero, o cuarto cuadrante.
. Dependiendo del ángulo, ese punto puede quedar en el primero, segundo, tercero, o cuarto cuadrante.
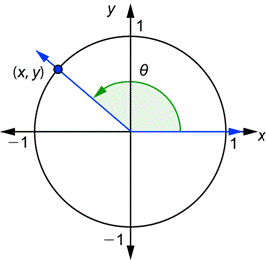
El seno del ángulo ![]() es igual a la coordenada-y de este punto y el coseno del ángulo
es igual a la coordenada-y de este punto y el coseno del ángulo ![]() es igual a la coordenada-x en este punto. De hecho, las seis funciones trigonométricas para cualquier ángulo
es igual a la coordenada-x en este punto. De hecho, las seis funciones trigonométricas para cualquier ángulo ![]() están ahora definidas por las seis ecuaciones anteriores.
están ahora definidas por las seis ecuaciones anteriores.
Los siguientes ejemplos te ayudarán a confirmar que cuando ![]() es un ángulo agudo, estas nuevas definiciones te dan los mismos resultados que las definiciones originales.
es un ángulo agudo, estas nuevas definiciones te dan los mismos resultados que las definiciones originales.
| Ejemplo | ||
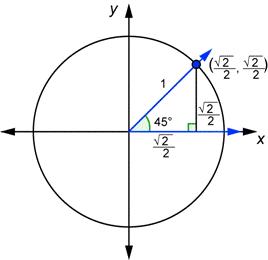
| Problema | Dibujar un ángulo de 45° en la posición estándar junto a un círculo unidad. Confirmar que las coordenadas x y y del punto de intersección del lado terminal y el círculo sean igual a | |
|
|
| Empieza con el triángulo 45° - 45° - 90°. Luego dibuja el ángulo de 45° en la posición estándar. |
|
|
| Este triángulo en el círculo unidad es similar al triángulo 45° - 45° - 90° . Cada longitud de un lado puede obtenerse dividiendo las longitudes del triángulo 45° - 45° - 90° entre |
|
|
De las coordenadas en un círculo unidad: Del triángulo: De las coordenadas en un círculo unidad: Del triángulo:
|
Observa las coordenadas x y y del punto en el círculo unidad. Luego usa el triángulo para encontrar
La coordenada-x es igual a
|
| Respuesta | Sí, |
|
En los siguientes dos ejemplos, las etiquetas de los ángulos 37° y 53° son en realidad buenas aproximaciones. La idea principal de los ejemplos (que esas fracciones con x y y son iguales con las funciones trigonométricas) se mantiene válida.
| Ejemplo | ||
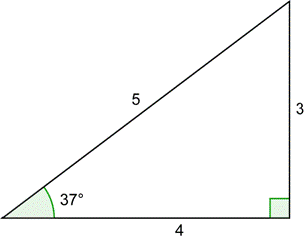
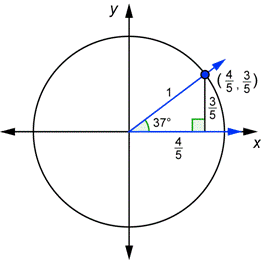
| Problema | Dibujar un ángulo de 37° en su posición estándar junto con un círculo unidad. Usa el triángulo siguiente para encontrar las coordenadas x y y del punto de intersección del lado terminal y el círculo. Calcula
| |
|
|
| Dibuja el ángulo de 37° en la posición estándar. El triángulo del círculo unidad es similar a un triángulo rectángulo 3-4-5. Como ésta hipotenusa es igual a la hipotenusa original dividida entre 5, puedes encontrar las longitudes de los catetos dividiendo la longitud original entre 5. |
|
|
| Encuentra las coordenadas x y y. |
|
|
| Calcula las razones. Compara los resultados con lo que obtienes de |
| Respuesta | Entonces sí, |
|
| Ejemplo | ||
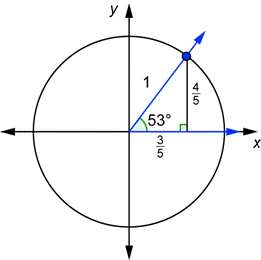
| Problema | Dibujar un ángulo de 53° en su posición estándar junto con un círculo unidad. Usa el triángulo siguiente para encontrar las coordenadas x y y del punto de intersección del lado terminal y el círculo. Calcula
| |
|
|
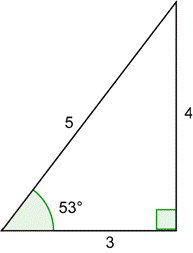
| Dibuja el ángulo de 53° en la posición estándar. El triángulo del círculo unidad es similar a un triángulo rectángulo 3-4-5. Como ésta hipotenusa es igual a la hipotenusa original dividida entre 5, puedes encontrar las longitudes de los catetos dividiendo la longitud original entre 5. |
|
|
| Encuentra las coordenadas x y y. |
|
|
| Calcula las razones. Compara los resultados con lo que obtienes de |
| Respuesta | Sí, |
|
Las primeras tres de nuestras nuevas definiciones nos llevan a una identidad importante:
![]()
Podemos reemplazar y por ![]() y x por
y x por ![]() en
en ![]() para obtener la identidad trigonométrica
para obtener la identidad trigonométrica ![]() .
.
![]()
Como la cotangente es la recíproca de la tangente, esto te da otra identidad trigonométrica.
|
|
Recuerda, una identidad es válida para cada valor posible de la variable. Por lo que no importa qué ángulo estás usando, los valores de la tangente y de la cotangente están dados por estos cocientes.
Si bien algunos libros te dan unas definiciones generales un poco distintas de las funciones trigonométricas, es importante saber que siempre te darán el los mismos valores que las definiciones que ya tenemos.
Por ejemplo, comienza con el radio de un círculo r (con el radio de 1) y un ángulo ![]() en la posición estándar. El lado terminal va a intersectar al círculo en un punto
en la posición estándar. El lado terminal va a intersectar al círculo en un punto ![]() . Ese punto podría estar en cualquier cuadrante, pero sólo mostramos el primer cuadrante.
. Ese punto podría estar en cualquier cuadrante, pero sólo mostramos el primer cuadrante.
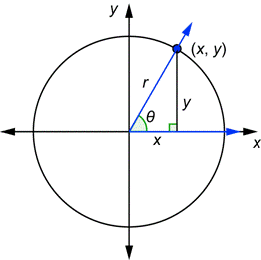
Ahora escribe las definiciones originales y luego reescríbelas usando las variables x, y, y r.
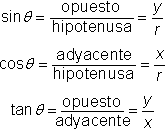
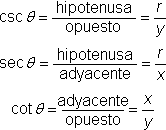
Estas seis fracciones se usan como las definiciones generales de las funciones trigonométricas para cualquier ángulo ![]() , en cualquier cuadrante.
, en cualquier cuadrante.
| Ejemplo | ||
| Problema | Calcular
| |
|
|
| El diagrama anterior contiene un triángulo 30° - 60° - 90°. La hipotenusa equivale al radio, por lo que es 10. El lado opuesto a 30° es la mitad de 10, o 5. El lado adyacente es |
|
|
| Los lados del triángulo te dan los valores de x y y en el primer diagrama. |
|
|
| Sustitúyelos en la definición. |
|
|
| Aquí está tu triángulo estándar 30° - 60° - 90°. |
|
|
| Calcula |
| Respuesta | Entonces sí, |
|
Se te han dado las definiciones “generales” de las seis funciones trigonométricas y has visto que, cuando calculas estas funciones usando ángulos agudos, el resultado es el mismo que lo que obtendrías usando las definiciones originales. Ahora aprenderás cómo aplicar éstas definiciones a ángulos que no son agudos y a ángulos negativos.
Dado cualquier ángulo ![]() , dibujarlo en la posición estándar junto con un círculo unidad. El lado terminal intersectará el círculo en algún punto
, dibujarlo en la posición estándar junto con un círculo unidad. El lado terminal intersectará el círculo en algún punto ![]() , como se muestra abajo.
, como se muestra abajo.

Aquí están de nuevo las definiciones generales de las seis funciones trigonométricas usando un círculo unidad.
|
|
Ahora usemos éstas definiciones con los ángulos 30°, 150°, 210°, y 330°. Ya los has hecho para el ángulo de 30°. Aquí vemos ese dibujo:
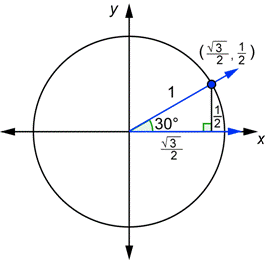
Los ángulos 150°, 210°, y 330° tienen algo en común. Cada uno de ellos tiene un ángulo de referencia de 30°, como puedes ver en el dibujo anterior. Gracias a esto, es fácil encontrar las coordenadas de los puntos donde los lados terminales intersectan al círculo unidad.
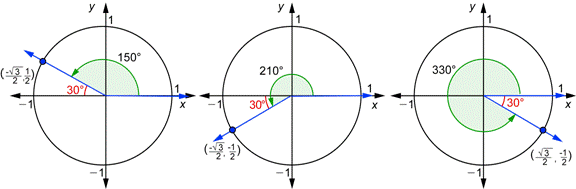
Para el ángulo de 150°, éste punto de intersección es la imagen opuesta de 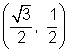 sobre el eje-y, por lo que las coordenadas para 150° son
sobre el eje-y, por lo que las coordenadas para 150° son 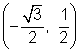 .
.
Para el ángulo de 210°, éste punto de intersección es la imagen opuesta de 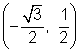 sobre el eje-x, por lo que las coordenadas para 210° son
sobre el eje-x, por lo que las coordenadas para 210° son 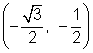 .
.
Para el ángulo de 330°, éste punto de intersección es la imagen opuesta de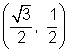 sobre el eje-x, por lo que las coordenadas para 330° son
sobre el eje-x, por lo que las coordenadas para 330° son 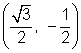 .
.
Puedes encontrar los valores de las seis funciones trigonométricas para 150°, 210°, y 330°. Tomemos algunas funciones trigonométricas y las evaluamos usando éstos ángulos. Por ejemplo, usando el diagrama de la izquierda y la definición de coseno:
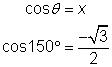
Usando el diagrama del centro y la definición de la cotangente:
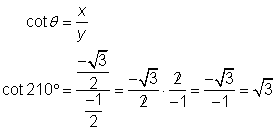
Usando el diagrama de la derecha y la definición de la cosecante:
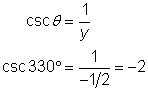
Si tomas el dibujo anterior con el ángulo de 30° en la posición estándar, y giras el ángulo para que el cateto más corto quede en el eje-x, obtienes el dibujo de un ángulo de 60° en la posición estándar, como vemos abajo.
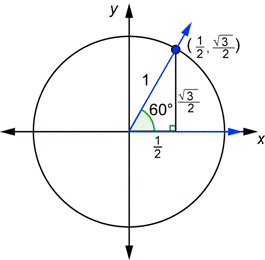
Puedes usar la información de éste diagrama para encontrar los valores de las seis funciones trigonométricas para cualquier ángulo que tenga como referencia el ángulo de 60°.
| Ejemplo | ||
| Problema | Determinar | |
|
|
| Dibuja el ángulo de 300° en la posición estándar y encuentra el ángulo de referencia. Encuentra la coordenada x del punto |
|
|
| Usa la definición del coseno. Sustituye el valor de la coordenada x que encontraste anteriormente. |
|
|
| Usa la definición de la secante. Sustituye el valor de la coordenada x que encontraste anteriormente. Observa que, al igual que con los ángulos agudos, la secante y el coseno son recíprocos. |
| Respuesta |
|
|
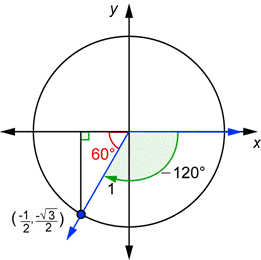
El procedimiento es el mismo incluso si el ángulo es negativo. Recuerda que un ángulo negativo es simplemente un ángulo con dirección a favor de las manecillas del reloj.
| Ejemplo | ||
| Problema | Encontrar los valores de | |
|
|
| Dibuja el ángulo de Como |
|
|
| Usa la definición del coseno. Sustituye el valor de la coordenada y que encontraste anteriormente. |
|
|
| Usa la definición de la cosecante. Sustituye el valor de la coordenada y que encontraste anteriormente. Observa que, al igual que con los ángulos agudos, la cosecante y el seno son recíprocos. |
| Respuesta |
|
|
Observa los resultados de os dos últimos ejemplos y nota lo siguiente:
En cada caso, el valor de la función trigonométrica fue igual al valor de la función para el ángulo de referencia (60°), o el negativo del valor de esa función para el ángulo de referencia. ¿Por qué sucedió esto? Los cálculos para 60° se hicieron usando el punto 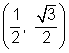 . Los cálculos para 300° y
. Los cálculos para 300° y ![]() se hicieron usando los puntos
se hicieron usando los puntos 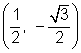 y
y 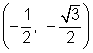 . Las coordenadas x tienen el mismo valor absoluto. Las coordenadas y también tienen el mismo valor absoluto. Cuando sustituyes en las expresiones x,
. Las coordenadas x tienen el mismo valor absoluto. Las coordenadas y también tienen el mismo valor absoluto. Cuando sustituyes en las expresiones x, ![]() , y, y
, y, y ![]() , el resultado será el mismo, o tendrá el signo negativo.
, el resultado será el mismo, o tendrá el signo negativo.
Obtendrás un resultado similar con otros ángulos. Entonces el procedimiento para encontrar el valor de la función trigonométrica se simplifica a lo siguiente:
|
Probemos éste procedimiento en el ejemplo siguiente.
| Ejemplo | ||
| Problema | Calcular | |
|
|
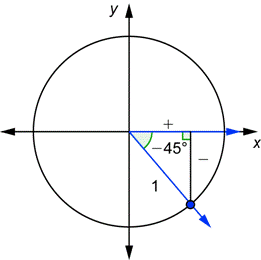
| Dibuja el ángulo en la posición estándar. El ángulo de referencia es 45°. |
|
|
| Usa el triángulo 45° - 45° - 90°. El valor de |
|
|
| En el primer diagrama, ponemos un signo |
|
|
| Como el resultado fue negativo, el valor de |
|
|
| Puedes seguir un procedimiento similar con la cotangente o usar el hecho de que es el recíproco de la tangente. |
| Respuesta |
|
|
Los ángulos cuya medida son un múltiplo de 90° tienen lados terminales en los ejes. Esto puede ser confuso, porque el lado terminal no está en un cuadrante, sino que en el límite entre cuadrantes. Entonces veamos éstos ángulos aparte. El dibujo siguiente muestra los puntos de intersección de los lados terminales de 0°, 90°, 180°, y 270° con el círculo unidad.
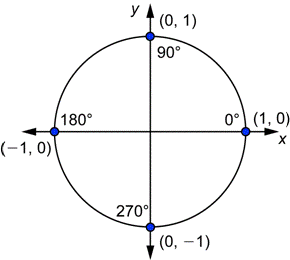
Puedes usar el dibujo y las definiciones para encontrar las funciones trigonométricas para 0°, 90°, 180°, y 270°. Por ejemplo:
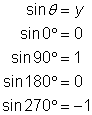
Para las seis funciones, sustituye los valores de x y y como hiciste anteriormente. Sin embargo, ¿qué pasa si intentas calcular ![]() usando la definición
usando la definición ![]() ?
?
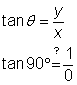
No puedes dividir entre 0, por lo que ![]() simplemente no está definida. De manera similar,
simplemente no está definida. De manera similar, ![]() tampoco está definida, porque si intentas aplicar la definición, terminarás dividiendo entre 0. Lo mismo sucede cada que una de las definiciones lleve a la división entre 0: la función trigonométrica no está definida para ese ángulo.
tampoco está definida, porque si intentas aplicar la definición, terminarás dividiendo entre 0. Lo mismo sucede cada que una de las definiciones lleve a la división entre 0: la función trigonométrica no está definida para ese ángulo.
| ¿Cuáles son los valores de
A) B) C) D)
|
Puedes usar las tablas siguientes para ayudarte a recordar los valores de las funciones trigonométricas para los ángulos de referencia 0°, 30°, 45°, 60°, y 90° para el seno y el coseno. Una vez que tienes éstas, puedes encontrar el valor de la tangente usando la identidad ![]() , y los valores de las otras tres funciones trigonométricas usando sus recíprocos.
, y los valores de las otras tres funciones trigonométricas usando sus recíprocos.
Construye la tabla como sigue:
|
| 0° | 30° | 45° | 60° | 90° |
| seno |
|
|
|
|
|
| coseno |
|
|
|
|
|
Como un paso inicial, escribe los números 0, 1, 2, 3, y 4 en la fila “seno” y los números 4, 3, 2, 1, y 0 en la fila “coseno”. Hazlo con un lápiz. ¡Vas a reemplazar éstos números!
|
| 0° | 30° | 45° | 60° | 90° |
| seno | 0 | 1 | 2 | 3 | 4 |
| coseno | 4 | 3 | 2 | 1 | 0 |
Ahora reemplaza los números del 0 al 4 sacando sus raíces cuadradas y dividiendo entre 2. Las filas ahora contienen los valores correctos, pero simplificados, para el seno y el coseno.
|
| 0° | 30° | 45° | 60° | 90° |
| seno |
|
|
|
|
|
| coseno |
|
|
|
|
|
Puedes simplificar ![]() como 0,
como 0, ![]() como 1, y
como 1, y ![]() como 2, y luego dividir entre 2. Esto te dará la tabla final con los valores correctos del seno y el coseno para los ángulos.
como 2, y luego dividir entre 2. Esto te dará la tabla final con los valores correctos del seno y el coseno para los ángulos.
|
| 0° | 30° | 45° | 60° | 90° |
| seno | 0 |
|
|
| 1 |
| coseno | 1 |
|
|
| 0 |
Primero aprendiste las definiciones de las funciones trigonométricas para un ángulo agudo. Luego aprendiste las definiciones generales para éstas funciones, que pueden usarse para cualquier ángulo, y el método para aplicarlas. Finalmente, aprenderás un procedimiento más simple para encontrar los valores de las funciones trigonométricas:
- Determinar el ángulo de referencia.
- Calcular el valor de la función trigonométrica del ángulo de referencia.
- Determinar si el valor de la función es positivo o negativo.
Ahora aprenderás una manera fácil de recordar cuándo son positivas las funciones trigonométricas y cuándo negativas.
La función seno: como ![]() , el seno es positivo cuando
, el seno es positivo cuando ![]() . Esto ocurre en los Cuadrantes I y II.
. Esto ocurre en los Cuadrantes I y II.
La función coseno: como ![]() , el coseno es positivo cuando
, el coseno es positivo cuando ![]() . Esto ocurre en los Cuadrantes I y IV.
. Esto ocurre en los Cuadrantes I y IV.
La función tangente: como ![]() , la tangente es positiva cuando x y y son ambas positivas o negativas. Esto ocurre en los cuadrantes I y III.
, la tangente es positiva cuando x y y son ambas positivas o negativas. Esto ocurre en los cuadrantes I y III.
Podemos resumir ésta información por cuadrante:
Cuadrante I: el seno, el coseno y la tangente son positivos.
Cuadrante II: el seno es positivo (el coseno y la tangente son negativos).
Cuadrante III: la tangente es positiva (el seno y el coseno son negativos).
Cuadrante IV: el coseno es positivo (el seno y la tangente son negativos).
Hay una regla nemotécnica sencilla para recordar esto usando la frase “TODAS SIN TACOS” y se desglosa de la siguiente forma: En el primer cuadrante “todas” son positivas. En el segundo cuadrante sólo es positivo el “seno” (sin en Inglés). En el tercer cuadrante sólo es positiva la “tangente”. En el cuarto cuadrante sólo es positivo el “coseno”.
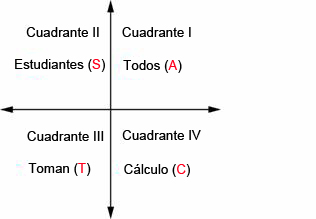
Ahora, si ves el Cuadrante II, por ejemplo, la palabra SIN te dice que el seno es positivo (mientras que el coseno y la tangente son negativos.
| Ejemplo | ||
| Problema | ¿Qué signo tienen | |
|
| Como | |
|
| La palabra sílaba TA en “TACOS” representa el hecho de que la tangente es positiva, entonces | |
|
| El seno y el coseno son negativos en el Cuadrante III, entonces | |
| Respuesta |
|
|
| Ejemplo | ||
| Problema | ¿En qué cuadrante está un ángulo si su seno es positivo y su tangente es negativa? | |
|
| Las palabras “TODAS” y “SIN” nos dicen que el seno es positivo en los Cuadrantes I y II. | |
|
| La tangente es positiva en el Cuadrante I, pero negativa en el Cuadrante II | |
| Respuesta | Cuadrante II |
|
Esto funciona para las funciones seno, coseno y tangente. Las otras tres funciones trigonométricas son recíprocas de éstas. Recuerda el hecho básico de que el recíproco de un número positivo es positivo, y el recíproco de un número negativo es negativo. Esto implica que el seno y la cosecante tienen el mismo signo, el coseno y la secante tienen el mismo signo, y la tangente y la cotangente tienen el mismo signo. Entonces si quieres conocer el signo de la cosecante, la secante, o la cotangente, encuentra el signo respectivo del seno, del coseno, o la tangente.
| ¿Qué signo tienen
A) Ambos son positivos. B) Ambos son negativos. C) D)
|
Sumario
Las funciones trigonométricas se definieron originalmente para ángulos agudos. Hay definiciones generales para éstas funciones, que aplican para ángulos de cualquier tamaño, incluyendo ángulos negativos. Los valores de las funciones trigonométricas se calculan encontrando el ángulo de referencia, determinando el valor de la función trigonométrica del ángulo de referencia, y luego determinando si el valor de la función es positivo o negativo. Una manera fácil de recordar el último paso es usando “TODAS SIN TACOS”