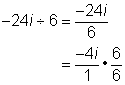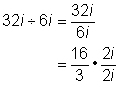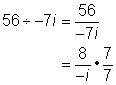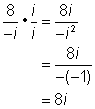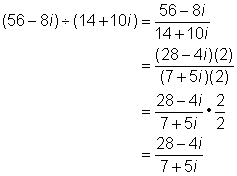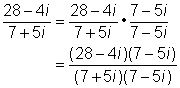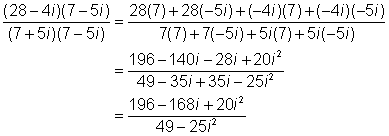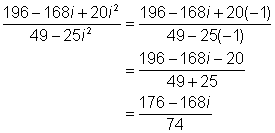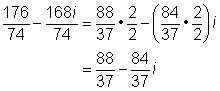Operaciones con números complejos

 

Objetivos de aprendizaje

·         Sumar números complejos.

·         Restar números complejos.

·         Multiplicar números complejos.

·         Encontrar conjugados de números complejos.

·         Dividir números complejos.

 

Cada vez que se presentan nuevos tipos de números, una de las primeras preguntas es, “¿Cómo se suman?” En este tema, aprenderás a sumar números complejos así como a restarlos, multiplicarlos y dividirlos.

 

Primero, considera la siguiente expresión.

 

(6x + 8) + (4x + 2)

 

Para simplificar esta expresión, combina los términos semejantes, 6x y 4x. Estos son los términos semejantes porque tienen la misma variable con el mismo exponente. De manera similar, 8 y 2 son términos semejantes porque ambos son constantes, sin variables.

 

(6x + 8) + (4x + 2) = 10x + 10

 

De la misma manera, puedes simplificar expresiones con radicales.

 

 

Puedes sumar  con  porque ambos términos tienen el mismo radical, , del mismo modo que 6x y 4x tienen la misma variable y exponente.

 

El número i parece una variable, pero recuerda que es igual a . Lo interesante es que no hay reglas nuevas de las cuales preocuparse, ya sea que lo trates como una variable o un radical, aplican las mismas reglas para sumar y restar números complejos. Combinas las partes imaginarias (los términos con i) y combinas las partes reales.

 

 

 

 

 

 

Restar. (5 + 3i) – (3 – i)   A) 2 + 4i   B) 6   C) 2 + 2i   D) 8 + 2i   Mostrar/Ocultar Respuesta A) 2 + 4i Correcto. Distribuir la resta en el segundo número complejo te da 5 + 3i – 3 + i. Reacomodando para juntar los términos comunes te da 5 – 3 + 3i + i y combinado los términos semejantes te da 2 + 4i.   B) 6 Incorrecto. Seguramente has combinado 5 + 3 del primer término (ignorando el i) y 3 – 1 del segundo término (ignorando el i), dando el resultado 8 - 2 = 6. Más bien, debes distribuir la resta en el segundo número complejo para obtener 5 + 3i – 3 + i. Reacomodando para poner juntar los términos semejantes da 5 – 3 + 3i + i y combinando términos semejantes da la respuesta correcta 2 + 4i.   C) 2 + 2i Incorrecto. Probablemente olvidaste distribuir la resta a la parte imaginaria del segundo número complejo, dejándolo como – i en lugar de + i. Distribuyendo la resta al segundo número complejo da 5 + 3i – 3 + i. Reacomodando para poner juntar los términos semejantes da 5 – 3 + 3i + i y combinando términos semejantes da la respuesta correcta 2 + 4i.   D) 8 + 2i Incorrecto. Seguramente sumaste en lugar de restar. Distribuyendo la resta al segundo número complejo da 5 + 3i – 3 + i. Reacomodando para poner juntar los términos semejantes da 5 – 3 + 3i + i y combinando términos semejantes da la respuesta correcta 2 + 4i.

 

 

De nuevo, considera la siguiente expresión. Antes de seguir leyendo, piensa en cómo la podrías simplificar.

 

(5x)(−3x)

 

Puedes simplificar multiplicando los coeficientes, luego las variables.

 

 

Multiplicar dos números imaginarios (¡pero no complejos!) funciona del mismo modo, pero hay un paso adicional. Empieza con el mismo método para multiplicar 5i y −3i.

 

 

 

Hasta ahora todo va bien, pero el i² se puede simplificar más.

 

Cuando multiplicas una raíz cuadrada por sí misma, obtienes el número dentro del radical. Esto es lo que significa una raíz cuadrada.

 

 

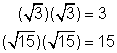
Bueno, i también es una raíz cuadrada. Es igual a .

 

 

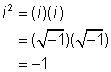
Entonces, el último paso para simplificar (5i)( −3i) = −15i² es reemplazar i² con −1.

 

 

 

 

 

¡Observa que el producto de dos números imaginarios es un número real! Veremos esto de nuevo cuando multipliquemos dos números complejos.

 

 

Multiplica y simplifica. (3i)( −i)   A) 3   B) −3   C) 3i   D) −3i2   Mostrar/Ocultar Respuesta A) 3 Correcto. (3i)( −i) = 3(-1)(i)(i) = −3i2 = −3(−1) = 3.   B) −3 Incorrecto. Probablemente no tomaste en cuenta el signo del segundo factor, o reemplazaste incorrectamente i2. (3i)( −i) = 3(−1)(i)(i) = −3i2 = −3(−1) = 3.   C) 3i Incorrecto. Probablemente multiplicaste incorrectamente (i)( −i), o reemplazaste incorrectamente i2. (3i)( −i) = 3(−1)(i)(i) = −3i2 = −3(−1) = 3.   D) −3i2 Incorrecto. Esta es una multiplicación, pero i2 puede simplificarse más. (3i)( −i) = 3(−1)(i)(i) = −3i2 = −3(−1) = 3.

 

 

La siguiente expresión es un poco más complicada porque se multiplican dos binomios. Esto significa que debes usar la Propiedad Distributiva de la Multiplicación. (Recuerda que multiplicar con el método FOIL — First, Outside, Inside, Last — es aplicar la propiedad distributiva de la multiplicación.) Una vez que los binomios han sido multiplicados, simplifica la expresión combinando los términos semejantes.

 

 

 

De nuevo, puedes multiplicar números complejos de la misma manera. Al final, necesitas simplificar i².

 

 

 

 

En este caso, el producto de dos números complejos es complejo. Pero en el siguiente ejemplo, el producto es real y no complejos. ¡Veamos si puedes averiguar por qué!

 

 

 

 

Así como  y  son conjugados, 6 + 8i y 6 – 8i son conjugados. (De nuevo, i es una raíz cuadrada, por lo que esto no es realmente algo nuevo.) Cuando los números son complejos, los llamamos conjugados complejos. Porque los conjugados tienen términos que son iguales excepto por la operación entre ellos (una es suma y la otra es resta), los términos i en el producto sumarán 0. En el ejemplo anterior, −48i se suma a 48i y esa suma es 0, por lo que no el término i no existe en el producto final. Esto significa que el producto de dos complejos conjugados siempre será un número real (y no complejo).

 

 

Multiplicar. (9 + i)(9 – i)   A) 82 + 18i   B) 80 – 18i   C) 80   D) 82   Mostrar/Ocultar Respuesta A) 82 + 18i Incorrecto. No olvides usar el método FOIL para que cada término en el primer número complejo se multiplique con cada término en el segundo número complejo. Como los factores son complejos conjugados, su producto será un número real. (9 + i)(9 – i) = 81 – 9i + 9i – i2 = 81 – i2 = 81 – (−1) = 81 + 1 = 82.   B) 80 – 18i Incorrecto. No olvides usar el método FOIL para que cada término en el primer número complejo se multiplique con cada término en el segundo número complejo. Como los factores son complejos conjugados, su producto será un número real. (9 + i)(9 – i) = 81 – 9i + 9i – i2 = 81 – i2 = 81 – (−1) = 81 + 1 = 82.   C) 80 Incorrecto. Probablemente multiplicaste correctamente pero olvidaste restar el i2, u olvidaste el negativo al multiplicar i y -i. (9 + i)(9 – i )= 81 – 9i + 9i – i2 = 81 – i2 = 81 – (−1) = 81 + 1 = 82.   D) 82 Correcto. (9 + i)(9 – i) = 81 – 9i + 9i – i2 = 81 – i2 = 81 – (−1) = 81 + 1 = 82.

 

 

Hasta ahora, cada operación con números complejos ha funcionado de la misma manera que con expresiones radicales. Esto no debería sorprenderte, el número i es el radical, después de todo, ¡por lo que los números complejos son expresiones radicales!

 

Veamos a la división en dos partes, como hicimos con la multiplicación. Primero, veamos la situación cuando el divisor es un monomio.

 

 

 

 

 

 

 

 

Simplifica. 12 ÷ 10i   A)   B)   C)   D)   Mostrar/Ocultar Respuesta A) Incorrecto. Cuando simplificas las partes numéricas de , todavía tienes i en el denominador. Racionaliza el denominador de  multiplicando por : .   B) Correcto. Después de simplificar las partes numéricas de , todavía tienes que racionalizar el denominador porque i queda en el denominador: .   C) Incorrecto. Cuando racionalizas el denominador, tienes i2 en el denominador. Como i2 = −1, el cociente es negativo. .   D) Incorrecto. Probablemente olvidaste el radical i en el denominador, o cometiste un error cuando racionalizaste el denominador. Cuando racionalizas el denominador, debes multiplicar también el numerador por i. .

 

 

Cuando el divisor (esto es, el denominador en la fracción) es un número complejo con partes real e imaginaria distintas de cero, debes racionalizar el denominador usando el conjugado complejo. Recuerda que el producto de un número complejo con su conjugado complejo siempre es un número real, por lo que el denominador será un número real. Esto significa que el resultado será equivalente, pero racionalizado.

 

 

 

 

Simplifica. (10 + 6i) ÷ (5 – 3i)   A)   B) 2 – 2i   C)   D)   Mostrar/Ocultar Respuesta A) Correcto. Escribe como una expresión racional y multiplica el numerador y el denominador por el conjugado complejo del divisor: . Esto se simplifica como .   B) 2 – 2i Incorrecto. Probablemente sólo dividiste las partes reales, luego dividiste los coeficientes de las partes imaginarias. Esto funciona en la suma y la resta, pero no en la división. Intenta escribir la división como una expresión racional y multiplica el numerador y el denominador por el conjugado complejo del divisor. La respuesta correcta es .   C) Incorrecto. Probablemente acomodaste incorrectamente la expresión racional para racionalizar: . Recuerda en este punto que i2 = −1, entonces restar 9i2 es lo mismo que sumar 9. La respuesta correcta es . D) Incorrecto. Probablemente acomodaste incorrectamente la expresión racional para racionalizar: . Recuerda que en este punto el denominador (34) divide ambos/i> términos en el numerador, entonces esto se simplifica como .

 

 

Operaciones con números complejos   Para sumar o restar, combinar términos semejantes.   Para multiplicar monomios, multiplicar los coeficientes y luego multiplicar los números imaginarios i. Si aparece i2, reemplazar con −1.   Para multiplicar números complejos que son binomios, usar la Propiedad Distributiva de la Multiplicación, o el método FOIL. Multiplicar los términos resultantes como monomios.   Para dividir, tratar el cociente como una fracción. ·         Simplificar las partes numéricas y luego racionalizar el denominador, si es necesario. ·         Reemplazar i2 por −1 en el numerador y el denominador, si es necesario. ·        Escribir la respuesta en la forma a + bi, que podría requerir más simplificación de a y b cuando son fracciones.

 

 

Los números complejos se pueden sumar, restar, multiplicar y dividir usando las mismas ideas que con los radicales y las variables. Con la multiplicación y la división, podrías necesitar reemplazar i² con −1 y continuar simplificando.