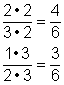Subtracting Fractions and Mixed Numbers

 

Learning Objectives

·         Subtract fractions with like and unlike denominators.

·         Subtract mixed numbers without regrouping.

·         Subtract mixed numbers with regrouping.

·         Solve application problems that require the subtraction of fractions or mixed numbers.

 

 

Sometimes subtraction, rather than addition, is required to solve problems that involve fractions. Suppose you are making pancakes and need  cups of flour but you only have  cups. How many additional cups will you have to get to make the pancakes? You can solve this problem by subtracting the mixed numbers.

 

 

The most simple fraction subtraction problems are those that have two proper fractions with a common denominator. That is, each denominator is the same. The process is just as it is for addition of fractions with like denominators, except you subtract! You subtract the second numerator from the first and keep the denominator the same.

 

Imagine that you have a cake with equal-sized pieces. Some of the cake has already been eaten, so you have a fraction of the cake remaining. You could represent the cake pieces with the picture below.

 

 

 

 

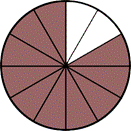
The cake is cut into 12 equal pieces to start. Two are eaten, so the remaining cake can be represented with the fraction . If three more pieces of cake are eaten, what fraction of the cake is left? You can represent that problem with the expression .

If you subtract 3 pieces, you can see below that  of the cake remains.

 

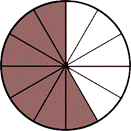
You can solve this problem without the picture by subtracting the numerators and keeping the denominator the same:

 

Subtracting Fractions with Like Denominators   If the denominators (bottoms) of the fractions are the same, subtract the numerators (tops) and keep the denominator the same. Remember to simplify the resulting fraction, if possible.

 

 

 

 

 

If the denominators are not the same (they have unlike denominators), you must first rewrite the fractions with a common denominator. The least common denominator, which is the least common multiple of the denominators, is the most efficient choice, but any common denominator will do. Be sure to check your answer to be sure that it is in simplest form. You can use prime factorization to find the least common multiple (LCM), which will be the least common denominator (LCD). See the example below.

 

 

 

The example below shows using multiples to find the least common multiple, which will be the least common denominator.

 

 

 

Subtract and simplify the answer.   A)   B)   C)   D)   Show/Hide Answer A) Incorrect. Find a least common denominator and subtract; then simplify. The correct answer is .   B) Incorrect. Simplify the fraction. The correct answer is .   C) Incorrect. Subtract, don’t add, the fractions. The correct answer is .   D) Correct. .

 

 

 

Subtracting mixed numbers works much the same way as adding mixed numbers. To subtract mixed numbers, subtract the whole number parts of the mixed numbers and then subtract the fraction parts in the mixed numbers. Finally, combine the whole number answer and the fraction answer to express the answer as a mixed number.

 

 

Sometimes it might be easier to express the mixed number as an improper fraction first and then solve. Consider the example below.

 

 

Since addition is the inverse operation of subtraction, you can check your answer to a subtraction problem with addition. In the example above, if you add  to your answer of , you should get .

 

Sometimes you have to find a common denominator in order to solve a mixed number subtraction problem.

 

 

 

Subtract. Simplify the answer and write it as a mixed number.     A)   B)   C)   D) 5   Show/Hide Answer A) Incorrect. Subtract the whole numbers, too. The correct answer is .   B) Correct. 9 – 4 = 5;   .  Combining them gives .   C) Incorrect. Subtract, don’t add, the fractions. The correct answer is .   D) 5 Incorrect. Subtract the fractions as well as the whole numbers. The correct answer is .

 

Sometimes when subtracting mixed numbers, the fraction part of the second mixed number is larger than the fraction part of the first number. Consider the problem: . The standard procedure would be to subtract the fractions, but  would result in a negative number. You don’t want that!  You can regroup one of the whole numbers from the first number, writing the first mixed number in a different way:

 

 

 

 

 

Now, you can write an equivalent problem to the original:

 

 

Then, you just subtract like you normally subtract mixed numbers:

 

6 – 3 = 3

So, the answer is .

 

As with many fraction problems, you may need to find a common denominator. Remember that a key part of adding and subtracting fractions and mixed numbers is making sure to have a common denominator as a first step! In the example below, the original fractions do not have a like denominator. You need to find one before proceeding with the next steps.

 

 

Sometimes a mixed number is subtracted from a whole number. In this case, you can also rewrite the whole number as a mixed number in order to perform the subtraction. You use an equivalent mixed number that has the same denominator as the fraction in the other mixed number.

 

 

 

 

Subtracting Mixed Numbers   If the fractional part of the mixed number being subtracted is larger than the fractional part of the mixed number from which it is being subtracted, or if a mixed number is being subtracted from a whole number, follow these steps:   1.      Subtract 1 from the whole number part of the mixed number being subtracted. 2.      Add that 1 to the fraction part to make an improper fraction. For example, . 3.      Then, subtract as with any other mixed numbers.   Alternatively, you can change both numbers to improper fractions and then subtract.

 

 

Subtract. Simplify the answer and write as a mixed number.   A)   B)   C)   D)   Show/Hide Answer A) Incorrect. This is the answer to . The fraction has to be subtracted from the 15. The correct answer is .   B) Incorrect. Subtract, don’t add, the quantities. The correct answer is .   C) Correct.     D) Incorrect. Subtract 1 from the whole number when rewriting it as a mixed number. The correct answer is .

 

 

 

Knowing how to subtract fractions and mixed numbers is useful in a variety of situations. When reading problems, look for key words that indicate that the problem can be solved using subtraction.

 

 

 

 

 

 

 

Mariah’s sunflower plant grew  inches in one week. Her tulip plant grew  inches in one week. How many more inches did the sunflower grow in a week than the tulip?   A)  inches   B)  inches   C) 15 inches   D)  inches   Show/Hide Answer A)  inches Incorrect. Subtract, don’t add, the fractions. The correct answer is  inches.   B)  inches Incorrect. Subtract , not . The correct answer is  inches.   C) 15 inches Incorrect. Subtract the fractions as well as the whole numbers in the mixed numbers. The correct answer is  inches.   D)  inches Correct. .

 

 

Subtracting fractions and mixed numbers combines some of the same skills as adding whole numbers and adding fractions and mixed numbers. When subtracting fractions and mixed numbers, first find a common denominator if the denominators are not alike, rewrite each fraction using the common denominator, and then subtract the numerators. When subtracting mixed numbers, if the fraction in the second mixed number is larger than the fraction in the first mixed number, rewrite the first mixed number by regrouping one whole as a fraction. Alternatively, rewrite all fractions as improper fractions and then subtract. This process is also used when subtracting a mixed number from a whole number.