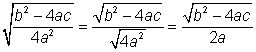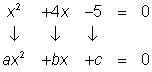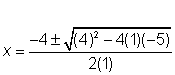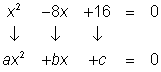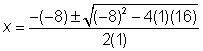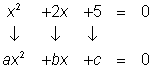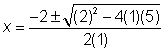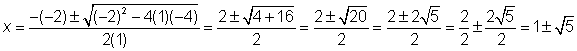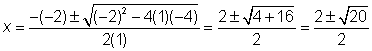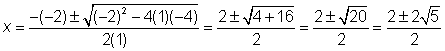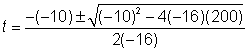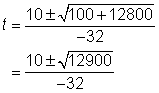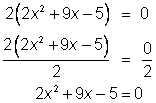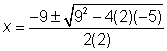The Quadratic Formula
Learning Objective(s)
· Write a quadratic equation in standard form and identify the values of a, b, and c in a standard form quadratic equation.
· Use the Quadratic Formula to find all real solutions.
· Use the Quadratic Formula to find all complex solutions.
· Compute the discriminant and state the number and type of solutions.
· Solve application problems requiring the use of the Quadratic Formula.
Introduction
You can solve any quadratic equation by completing the square—rewriting part of the equation as a perfect square trinomial. If you complete the square on the generic equation ax2 + bx + c = 0 and then solve for x, you find that ![]() . This equation is known as the Quadratic Formula.
. This equation is known as the Quadratic Formula.
This formula is very helpful for solving quadratic equations that are difficult or impossible to factor, and using it can be faster than completing the square. The Quadratic Formula can be used to solve any quadratic equation of the form ax2 + bx + c = 0.
The form ax2 + bx + c = 0 is called standard form of a quadratic equation. Before solving a quadratic equation using the Quadratic Formula, it's vital that you be sure the equation is in this form. If you don't, you might use the wrong values for a, b, or c, and then the formula will give incorrect solutions.
| Example | |||||||||||||||||||||||
| Problem | Rewrite the equation 3x + 2x2 + 4 = 5 in standard form and identify a, b, and c. | ||||||||||||||||||||||
|
| 3x + 2x2 + 4 = 5 3x + 2x2 + 4 – 5 = 5 – 5 | First be sure that the right side of the equation is 0. In this case, all you need to do is subtract 5 from both sides. | |||||||||||||||||||||
|
| 3x + 2x2 – 1 = 0 2x2 + 3x – 1 = 0 | Simplify, and write the terms with the exponent on the variable in descending order. | |||||||||||||||||||||
|
|
a = 2, b = 3, c = −1
| Now that the equation is in standard form, you can read the values of a, b, and c from the coefficients and constant. Note that since the constant 1 is subtracted, c must be negative. | |||||||||||||||||||||
| Answer | 2x2 + 3x – 1 = 0; a = 2, b = 3, c = −1 | ||||||||||||||||||||||
| Example | |||||||||||||||||||||||
| Problem | Rewrite the equation 2(x + 3)2 – 5x = 6 in standard form and identify a, b, and c. | ||||||||||||||||||||||
|
| 2(x + 3)2 – 5x = 6 2(x + 3)2 – 5x – 6 = 6 – 6 | First be sure that the right side of the equation is 0. | |||||||||||||||||||||
|
| 2(x2 + 6x + 9) – 5x – 6 = 0 2x2 + 12x + 18 – 5x – 6 = 0 2x2 + 12x – 5x + 18 – 6 = 0 2x2 + 7x + 12 = 0 | Expand the squared binomial, then simplify by combining like terms.
Be sure to write the terms with the exponent on the variable in descending order. | |||||||||||||||||||||
|
|
a = 2, b = 7, c = 12
| Now that the equation is in standard form, you can read the values of a, b, and c from the coefficients and constant. | |||||||||||||||||||||
| Answer | 2x2 + 7x + 12 = 0; a = 2, b = 7, c = 12 | ||||||||||||||||||||||
| Identify the values of a, b, and c in the standard form of the equation 3x + x2 = 6.
A) a = 3, b = 1, c = 6 B) a = 1, b = 3, c = 6 C) a = 1, b = 3, c = −6 D) a = 3, b = 1, c = −6
|
Deriving the Quadratic Formula
Let's complete the square on the general equation and see exactly how that produces the Quadratic Formula. Recall the process of completing the square.
· Start with an equation of the form x2 + bx + c = 0.
· Rewrite the equation so that x2 + bx is isolated on one side.
· Complete the square by adding ![]() to both sides.
to both sides.
· Rewrite the perfect square trinomial as a square of a binomial.
· Use the Square Root Property and solve for x.
Can you complete the square on the general quadratic equation ax2 + bx + c = 0? Try it yourself before you continue to the example below. Hint: Notice that in the general equation, the coefficient of x2 is not equal to 1. You can divide the equation by a, which makes some of the expressions a bit messy, but if you are careful, everything will work out, and at the end, you’ll have the Quadratic Formula!
| Example | |||
| Problem | Complete the square of ax2 + bx + c = 0 to arrive at the Quadratic Formula. | ||
|
|
|
| Divide both sides of the equation by a, so that the coefficient of x2 is 1. |
|
|
|
| Rewrite so the left side is in form x2 + bx (although in this case bx is actually |
|
|
|
| Since the coefficient on x is |
|
|
|
| Write the left side as a binomial squared. |
|
|
|
| Evaluate |
|
|
|
| Write the fractions on the right side using a common denominator. |
|
|
|
| Add the fractions on the right. |
|
|
|
| Use the Square Root Property. Remember that you want both the positive and negative square roots! |
|
|
|
| Subtract |
|
|
|
| The denominator under the radical is a perfect square, so:
|
| Answer |
|
| Add the fractions since they have a common denominator. |
There you have it, the Quadratic Formula.
The Quadratic Formula will work with any quadratic equation, but only if the equation is in standard form, ![]() . To use it, follow these steps.
. To use it, follow these steps.
· Put the equation in standard form first.
· Identify the coefficients, a, b, and c. Be careful to include negative signs if the bx or c terms are subtracted.
· Substitute the values for the coefficients into the Quadratic Formula.
· Simplify as much as possible.
· Use the ± in front of the radical to separate the solution into two values: one in which the square root is added, and one in which it is subtracted.
· Simplify both values to get the possible solutions.
That's a lot of steps. Let’s try using the Quadratic Formula to solve a relatively simple equation first; then you’ll go back and solve it again using another factoring method.
| Example | |||
| Problem | Use the Quadratic Formula to solve the equation x2 + 4x = 5. | ||
|
| x2 + 4x = 5 x2 + 4x – 5 = 0 |
| First write the equation in standard form. |
|
|
|
| a = 1, b = 4, c = −5
Note that the subtraction sign means the constant c is negative. |
|
|
|
| Substitute the values into the Quadratic Formula. |
|
|
|
| Simplify, being careful to get the signs correct. |
|
|
|
| Simplify some more. |
|
|
|
| Simplify the radical: |
|
|
or
|
| Separate and simplify to find the solutions to the quadratic equation. Note that in one, 6 is added and in the other, 6 is subtracted. |
| Answer | x = 1 or −5 |
|
|
You can check these solutions by substituting 1 and −5 into the original equation.
| x = 1 | x = −5 |
| x2 + 4x = 5 | x2 + 4x = 5 |
| (1)2 + 4(1) = 5 | (−5)2 + 4(−5) = 5 |
| 1 + 4 = 5 | 25 ‒ 20 = 5 |
| 5 = 5 | 5 = 5 |
You get two true statements, so you know that both solutions work: x = 1 or −5. You’ve solved the equation successfully using the Quadratic Formula!
However, upon looking at x2 + 4x = 5, you may have thought “I already know how to do this; I can rewrite this equation as x2 + 4x – 5 = 0, and then factor it as (x + 5)(x – 1) = 0, so x = −5 or 1.” This is correct—and congratulations if you made this connection!
Sometimes, it may be easier to solve an equation using conventional factoring methods, like finding number pairs that sum to one number (in this example, 4) and that produce a specific product (in this example −5) when multiplied. The power of the Quadratic Formula is that it can be used to solve any quadratic equation, even those where finding number combinations will not work.
Most of the quadratic equations you've looked at have two solutions, like the one above. The following example is a little different.
| Example | |||
| Problem | Use the Quadratic Formula to solve the equation x2 – 2x = 6x – 16. | ||
|
| x2 – 2x = 6x – 16 x2 – 2x – 6x + 16 = 0 x2 – 8x + 16 = 0 |
| Subtract 6x from each side and add 16 to both sides to put the equation in standard form. |
|
|
|
| Identify the coefficients a, b, and c. x2 = 1x2, so a = 1. Since 8x is subtracted, b is negative.
a = 1, b = −8, c = 16 |
|
|
|
|
Substitute the values into the Quadratic Formula. |
|
|
|
| Simplify. |
|
|
|
| Since the square root of 0 is 0, and both adding and subtracting 0 give the same result, there is only one possible value. |
| Answer | x = 4 |
|
|
Again, check using the original equation.
| x2 – 2x = 6x – 16 |
| (4)2 – 2(4) = 6(4) – 16 |
| 16 – 8 = 24 – 16 |
| 8 = 8 |
Let's try one final example. This one also has a difference in the solution.
| Example | |||
| Problem | Use the Quadratic Formula to solve the equation x2 + 2x = −5. | ||
|
| x2 + 2x = −5 x2 + 2x + 5 = 0 |
| First write the equation in standard form. |
|
|
|
| a = 1, b = 2, c = 5
|
|
|
|
|
Substitute the values into the Quadratic Formula. |
|
|
|
| Simplify, being careful to get the signs correct. |
|
|
|
| Simplify some more. |
|
|
|
| Simplify the radical, but notice that the number under the radical symbol is negative! The square root of −16 is imaginary. |
|
|
or
|
| Separate and simplify to find the solutions to the quadratic equation. |
| Answer | x = −1 + 2i or −1 – 2i |
|
|
Check these solutions in the original equation. Be careful when expanding the squares and replacing i2 with -1.
| x = −1 + 2i | x = −1 – 2i |
| x2 + 2x = −5 | x2 + 2x = −5 |
| (−1+2i)2 + 2(−1 + 2i) = −5 | (−1 – 2i)2 + 2(−1 – 2i) = −5 |
| 1 – 4i + 4i2 – 2 + 4i = −5 | 1 + 4i + 4i2 – 2 – 4i = −5 |
| 1 – 4i + 4(−1) – 2 + 4i = −5 | 1 + 4i + 4(-1) – 2 – 4i = −5 |
| 1 – 4 – 2 = −5 | 1 – 4 – 2 = −5 |
| −5 = −5 | −5 = −5 |
| Use the Quadratic Formula to solve the equation x2 – 2x – 4 = 0.
A) x = 2 B) x =11, x = −9 C) D)
|
These examples have shown that a quadratic equation may have two real solutions, one real solution, or two complex solutions.
In the Quadratic Formula, the expression underneath the radical symbol determines the number and type of solutions the formula will reveal. This expression, b2 – 4ac, is called the discriminant of the equation ax2 + bx + c = 0.
Let’s think about how the discriminant affects the evaluation of ![]() , and how it helps to determine the solution set.
, and how it helps to determine the solution set.
· If b2 – 4ac > 0, then the number underneath the radical will be a positive value. You can always find the square root of a positive, so evaluating the Quadratic Formula will result in two real solutions (one by adding the positive square root, and one by subtracting it).
· If b2 – 4ac = 0, then you will be taking the square root of 0, which is 0. Since adding and subtracting 0 both give the same result, the "±" portion of the formula doesn't matter. There will be one real solution.
· If b2 – 4ac < 0, then the number underneath the radical will be a negative value. Since you cannot find the square root of a negative number using real numbers, there are no real solutions. However, you can use imaginary numbers. You will then have two complex solutions, one by adding the imaginary square root and one by subtracting it.
| Example | |||
| Problem | Use the discriminant to determine how many and what kind of solutions the quadratic equation x2 – 4x + 10 = 0 has. |
| |
|
| b2 – 4ac (−4)2 – 4(1)(10) | Evaluate b2 – 4ac. First note that a = 1, b = −4, and c = 10. | |
|
| 16 – 40 = −24 | The result is a negative number. The discriminant is negative, so the quadratic equation has two complex solutions. | |
| Answer | The quadratic equation x2 – 4x + 10 = 0 has two complex solutions. | ||
| Suppose a quadratic equation has a discriminant that evaluates to zero. Which of the following statements is always true?
A) The equation has two solutions. B) The equation has one solution. C) The equation has zero solutions.
|
Quadratic equations are widely used in science, business, and engineering. Quadratic equations are commonly used in situations where two things are multiplied together and they both depend on the same variable. For example, when working with area, if both dimensions are written in terms of the same variable, you use a quadratic equation. Because the quantity of a product sold often depends on the price, you sometimes use a quadratic equation to represent revenue as a product of the price and the quantity sold. Quadratic equations are also used when gravity is involved, such as the path of a ball or the shape of cables in a suspension bridge.
A very common and easy-to-understand application is the height of a ball thrown at the ground off a building. Because gravity will make the ball speed up as it falls, a quadratic equation can be used to estimate its height any time before it hits the ground. Note: The equation isn't completely accurate, because friction from the air will slow the ball down a little. For our purposes, this is close enough.
| Example | |||
| Problem | A ball is thrown off a building from 200 feet above the ground. Its starting velocity (also called initial velocity) is −10 feet per second. (The negative value means it's heading toward the ground.)
The equation h = −16t2 – 10t + 200 can be used to model the height of the ball after t seconds. About how long does it take for the ball to hit the ground? | ||
|
| h = -16t2 – 10t + 200
0 = -16t2 – 10t + 200
−16t2 – 10t + 200 = 0 |
| When the ball hits the ground, the height is 0. Substitute 0 for h.
|
|
|
|
| This equation is difficult to solve by factoring or by completing the square, so solve it by applying the Quadratic Formula, |
|
|
|
| Simplify. Be very careful with the signs. |
|
| t is approximately −3.86 or 3.24. |
| Use a calculator to find both roots.
Consider the roots logically. One solution, −3.86, cannot be the time because it is a negative number. The other solution, 3.24 seconds, must be when the ball hits the ground. |
| Answer | The ball hits the ground approximately 3.24 seconds after being thrown. | ||
The area problem below does not look like it includes a Quadratic Formula of any type, and the problem seems to be something you have solved many times before by simply multiplying. But in order to solve it, you will need to use a quadratic equation.
| Example | |||
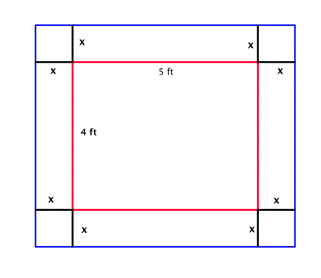
| Problem | Bob made a quilt that is 4 ft x 5 ft. He has 10 sq. ft. of fabric he can use to add a border around the quilt. How wide should he make the border to use all the fabric? (The border must be the same width on all four sides.) | ||
|
|
| Sketch the problem. Since you don’t know the width of the border, you will let the variable x represent the width.
In the diagram, the original quilt is indicated by the red rectangle. The border is the area between the red and blue lines. | |
|
|
|
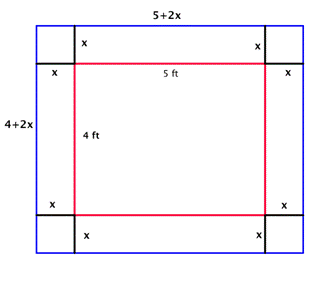
Since each side of the original 4 by 5 quilt has the border of width x added, the length of the quilt with the border will be 5 + 2x, and the width will be 4 + 2x.
(Both dimensions are written in terms of the same variable, and you will multiply them to get an area! This is where you might start to think that a quadratic equation might be used to solve this problem.) | |
| Area of border = Area of the blue rectangle minus the area of the red rectangle
Area of border = (4 + 2x)(5 + 2x) – (4)(5)
|
| You are only interested in the area of the border strips. Write an expression for the area of the border. | |
|
10 = (4 + 2x)(5 + 2x) – 20 |
| There are 10 sq ft of fabric for the border, so set the area of border to be 10. | |
|
10 = 20 + 8x + 10x + 4x2 – 20 |
|
Multiply (4 + 2x)(5 + 2x). | |
|
10 = 18x + 4x2 |
|
Simplify. | |
|
0 = 18x + 4x2 – 10 or 4x2 + 18x – 10 = 0
2(2x2 + 9x – 5) = 0
|
| Subtract 10 from both sides so that you have a quadratic equation in standard form and can apply the Quadratic Formula to find the roots of the equation.
Factor out the greatest common factor, 2, so that you can work with the simpler equivalent equation, 2x2 + 9x – 5 = 0. | |
|
|
| Use the Quadratic Formula. In this case, a = 2, b = 9, and c = −5. | |
|
|
|
Simplify. | |
|
or
|
| Find the solutions, making sure that the ± is evaluated for both values.
| |
|
Answer |
The width of the border should be 0.5 ft. | Ignore the solution x = −5, since the width could not be negative. | |
| A ball is launched upward at 48 feet/second from a platform that is 100 feet high. The equation giving its height t seconds after launch is h = −16t2 + 48t + 100. The ball will shoot up to 136 feet high, then begin to come back down. About how long will the ball take to get to that maximum height?
A) 1.5 seconds B) 3.6 seconds C) 4.4 seconds D) This problem cannot be solved.
|
Summary
Quadratic equations can appear in different applications. The Quadratic Formula is a useful way to solve these equations, or any other quadratic equation! The Quadratic Formula, ![]() , is found by completing the square of the quadratic equation
, is found by completing the square of the quadratic equation ![]() .
.
The discriminant of the Quadratic Formula is the quantity under the radical, ![]() . It determines the number and the type of solutions that a quadratic equation has. If the discriminant is positive, there are 2 real solutions. If it is 0, there is 1 real solution. If the discriminant is negative, there are 2 complex solutions (but no real solutions).
. It determines the number and the type of solutions that a quadratic equation has. If the discriminant is positive, there are 2 real solutions. If it is 0, there is 1 real solution. If the discriminant is negative, there are 2 complex solutions (but no real solutions).