Rate of Change and Slope
Learning Objective(s)
· Calculate the rate of change or slope of a linear function given information as sets of ordered pairs, a table, or a graph.
· Apply the slope formula.
Introduction
We experience slopes every day. Think about biking down a hill or climbing a set of stairs. Both the hill and the stairs have a slope. That means that as we travel along them, we are moving in two directions at the same time—sideways, and either up or down. In conversation, we use words like gentle or steep to describe the slope of the ground or an object. Along a gentle slope, most of the movement is horizontal. Along a steep slope, the vertical movement is greater.
Slope Formula
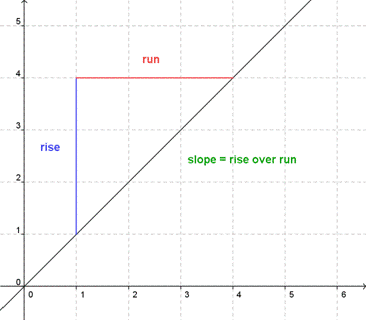
The mathematical definition of slope is very similar to our everyday one. In math, slope is the ratio of the vertical and horizontal changes between two points on a surface or a line. The vertical change between two points is called the rise, and the horizontal change is called the run. The slope equals the rise divided by the run: ![]() . This simple equation is called the slope formula.
. This simple equation is called the slope formula.
The slope formula is often shortened to the phrase “rise over run.” Although it sounds simple, the slope formula is a powerful tool for calculating and comparing the steepness of landscapes, structures, and lines.
What is the slope formula?
A) The vertical change divided by the horizontal change between two points on a line.
B) Rise minus run
C) The sideways movement over the up or down movement along a line or surface.
D) gentle or steep
We can find the slope of a line on a graph by counting off the rise and the run between two points. If a line rises 4 units for every 1 unit that it runs, the slope is 4 divided by 1, or 4. A large number like this indicates a steep slope: in this case, the slope goes 4 steps up for every one step sideways.
If a line rises 2 units while it runs 8 units, the slope is 2 divided by 8, or ¼. A small number like this represents a gentle slope. This line goes up only 1 step while it travels 4 steps to the side.
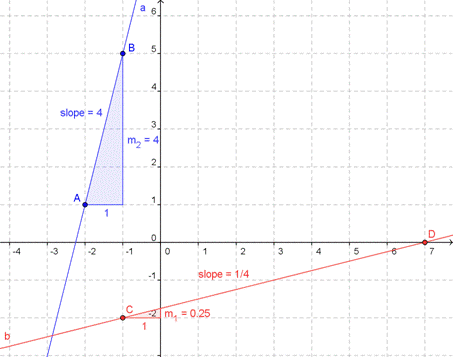
The ratio of rise over run describes the slope of all straight lines. This ratio is constant between any two points along a straight line, which means that the slope of a straight line is constant, too, no matter where it is measured along the line.
Slope Formula and Coordinates
It’s easy to find the slope of a line on a graph by measuring the rise and the run. We can also find the slope of a straight line if we know the coordinates of any two points on that line. Every point has a set of coordinates: a y-value and an x-value, written as (x, y). The x value tells us where a point is horizontally. The y value tells us where the point is vertically.
Consider two random points on a line. We’ll call them point 1 and point 2. Point 1 has coordinates (x1, y1) and point 2 has coordinates (x2, y2).
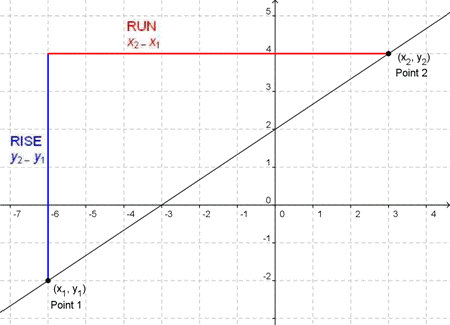
The rise is the vertical distance between the two points, which is the difference between their y-coordinates. That makes the rise y2 − y1. The run between these two points is the difference in the x-coordinates, or x2 − x1. Since slope equals rise over run, the slope of the line is y2 − y1 over x2 − x1. We’ve now got a new way to write the slope formula and to calculate the value of a slope. Slope is the difference between the y-coordinates divided by the difference between the x-coordinates.
Mathematicians commonly use the letter m to represent slope. So this is how you will most often see the slope formula written in algebra: ![]() . At heart, though, this is still the simple equation of slope = rise over run.
. At heart, though, this is still the simple equation of slope = rise over run.
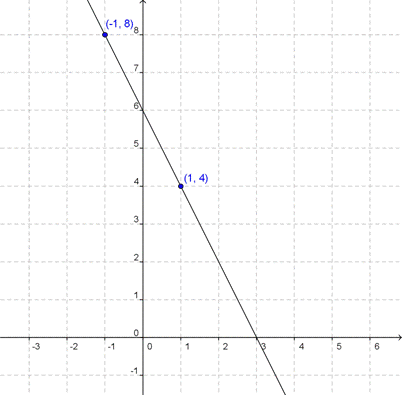
Let’s use the slope formula to calculate the slope of a line, using just the coordinates of two points. The line passes through the points (1, 4) and (-1, 8). Let’s call the point (1, 4) point 1, and the point (-1, 8) point 2. That means x1 = 1, y1 = 4, x2 = -1, and y2 = 8.
| Example | |
| Points | Coordinates |
| (1, 4) | x1 = 1 y1 = 4 |
| (-1, 8) | x2 = -1 y2 = 8 |
The slope formula is ![]() . When we put the coordinates into the formula, we get the equation
. When we put the coordinates into the formula, we get the equation ![]() . This reduces to m = -2. The slope of the line is -2.
. This reduces to m = -2. The slope of the line is -2.
It is important to realize that it doesn’t matter which point is designated as 1 and which is 2. We could have called (-1, 8) point 1, and (1, 4) point 2. In that case, putting the coordinates into the slope formula produces the equation ![]() . Once again, that simplifies to m = -2. That’s the same slope as before.
. Once again, that simplifies to m = -2. That’s the same slope as before.
What is the slope of the line between the points (-2, 1) and (1, 3)?
A) 2/3
B) -2
C) -2/3
D) 3/2
Slope of Horizontal and Vertical Lines
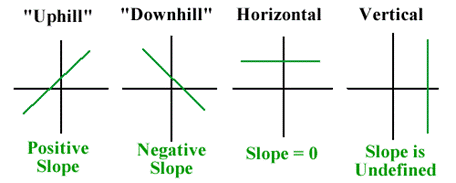
So far we’ve considered lines that run “uphill” or “downhill.” Their slopes may be large or small, but they are always positive or negative numbers. But there are two other kinds of lines, horizontal and vertical. What is the slope of a flat line or level ground? Of a sheer wall or a vertical line?
Let’s consider a horizontal line on a graph. No matter which two points we choose on the line, they will always have the same y-coordinate.
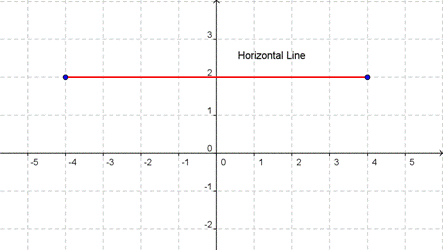
That means the rise, the vertical difference between two points, will always be zero. That makes sense—a horizontal line doesn’t go up or down. What happens when we put a rise of 0 into the slope formula? It becomes ![]() . Zero divided by any number is zero. The slope of a horizontal line is always 0.
. Zero divided by any number is zero. The slope of a horizontal line is always 0.
How about vertical lines? In their case, no matter which two points we choose, they will always have the same x-coordinate,
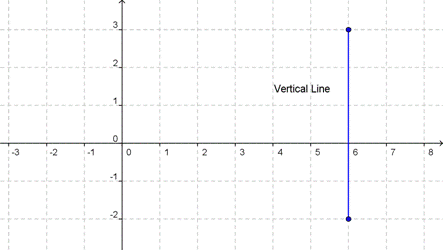
That means that the run, the horizontal difference between two points, will always be zero. That makes sense—a vertical line doesn’t go sideways at all. When we put a run of 0 into the slope formula, the equation becomes ![]() . We can’t calculate that value because division by zero has no meaning in the set of real numbers. All vertical lines have a slope that is undefined.
. We can’t calculate that value because division by zero has no meaning in the set of real numbers. All vertical lines have a slope that is undefined.
Summary
As you can see, slopes play an important role in our everyday life. You may walk up a slope to get to the bus stop or ski down the slope of a mountain. The slope formula, written ![]() , is a useful tool you can use to calculate the vertical and horizontal change of a variety of slopes.
, is a useful tool you can use to calculate the vertical and horizontal change of a variety of slopes.
