Nonlinear Functions
Learning Objective(s)
· Define nonlinear function.
· Define inverse functions and recognize them in equation, table, and graph form.
· Define quadratic functions and recognize them in equation, table, and graph form.
· Define exponential functions and recognize them in equation, table, and graph form.
Have you ever baked cookies? You can’t touch one right when they come out of the oven, or you’ll burn yourself. It doesn’t take long for them to cool off enough so you can eat them, but they’ll still stay warm for a long time. And they don’t get cooler than room temperature. If we drew a graph of the cookie cooling situation, it would look something like this:
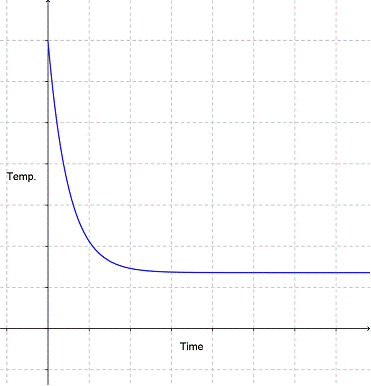
Notice that the graph is steepest in the beginning and then levels off as time goes on, until the cookies are room temperature. This is a function—there is an input and an output, and as time (the input) changes, so does temperature (the output). But it isn’t a linear function, because it doesn’t follow a straight line. Any function that isn’t linear is called a nonlinear function—that should be easy to remember!
There are many kinds of nonlinear functions. We’re going to explore just a few of these.
One kind of nonlinear function is called inverse variation. In these functions, the dependent variable equals a constant times the inverse of the independent variable. In symbolic form, this is the equation ![]() , where y is the dependent variable, k is the constant, and x is the independent variable. Compare this with the equation for a function that has direct variation between the variables, such as the proportional function formula of
, where y is the dependent variable, k is the constant, and x is the independent variable. Compare this with the equation for a function that has direct variation between the variables, such as the proportional function formula of ![]() . The only difference is that the inverse of the input is used for inverse variation functions (another name that makes perfect sense).
. The only difference is that the inverse of the input is used for inverse variation functions (another name that makes perfect sense).
One example of an inverse function is the speed required to travel between two cities in a given amount of time.
Let’s say you need to drive from Boston to Chicago, which is about 1,000 miles. The more time you have, the slower you can go. If you want to get there in 20 hours, you need to go 50 miles per hour, because ![]() . But if you can take 40 hours to get there, you only have to average 25 miles per hour, since
. But if you can take 40 hours to get there, you only have to average 25 miles per hour, since ![]() . The equation for figuring out how fast to drive from the amount of time you have is
. The equation for figuring out how fast to drive from the amount of time you have is ![]() , or
, or ![]() . See—this is the same form as the inverse variation function formula,
. See—this is the same form as the inverse variation function formula, ![]() .
.
Here’s a table that shows several times and speeds that satisfy the equation:
| Time | Speed (miles per hour) |
| 1 | 1,000 |
| 5 | 200 |
| 10 | 100 |
| 15 | 66 2/3 |
| 16 | 62 1/2 |
| 20 | 50 |
| 40 | 25 |
Now if we plot those points, we’ll see that the graph is definitely not a straight line.
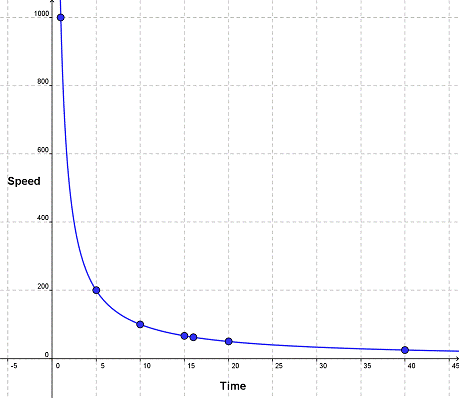
An important part of functions and their graphs is the rate of change. What is happening with the rate of change in this graph? When time is close to 0, a small change in time produces a large drop in the rate you’d need to travel. If you have very little time, say 1 hour, you’d have to drive 1000 miles an hour to make it, and I’m pretty sure that’s illegal. But if you can take just 1 hour more, you can cut your speed by 500 miles an hour.
Now look at the middle of the graph. The graph is getting shallow here—a change of an hour isn’t going to make much difference in speed. If you drive for 15 hours, you’ll need to go almost 67 mph. Add an extra hour and this time the speed required drops by only about 4 miles per hour.
The rate of change in this graph is not constant. It starts very high, so the graph is very steep. But as the graph rate of change gets smaller, the graph levels out.
Another kind of nonlinear function is a quadratic function. In a quadratic function, the independent variable (x) is multiplied by itself—in many cases, it’s squared. (The name comes from the Latin word for square. That’s not nearly as helpful as nonlinear and inverse, is it?).
Let’s look at the simplest quadratic function, which has the equation of y = x2. A table of x and y values of this function might look like this:
| x | Y |
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
On a graph, these values form a curved, U-shaped line called a parabola.
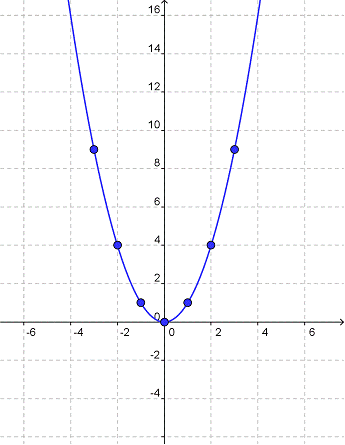
All quadratic functions form a parabola on a graph. The parabola may open upwards (like this – U) or downwards (like this – ∩), be wide or narrow, be symmetrical around the y-axis or lie off in one of the quadrants. Quadratic functions are used to describe things with smooth symmetrical curves, like the path of a bouncing ball or the arch of a bridge.
A quadratic function can have the equation y = x2. But other quadratic function formulas are more complex—these are all quadratic equations:
| y = ax2 + bx + c |
| y = (ax + b)(cx + d) |
| y = a(x+b)2 + c |
The important thing to notice here is that in each equation, the independent variable is multiplied by itself. The letters a, b, c, and d are coefficients—their presence in the equation modifies the shape and location of the parabola.
Confused? Try this—the interactive graph below lets you change the values of a, b, and c in the standard quadratic formula y = ax2 + bx + c. Click and drag the sliders labeled a, b, and c, and see what happens to the parabola.
The graph below shows the function height off the ground over time for a ball that you toss in the air and catch.
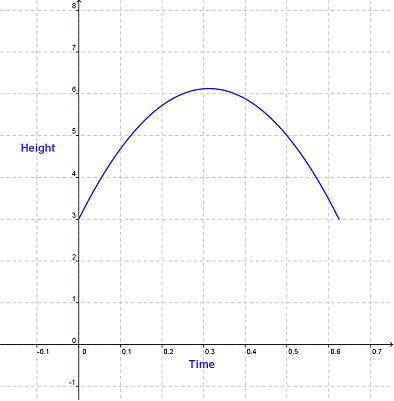
Based on this graph, which of the following statements is true?
A) The higher the ball is, the more slowly it is moving.
B) The ball travels at a constant rate of speed.
C) The ball rises faster than it falls.
D) The ball falls faster than it rises.
Another type of nonlinear function is the exponential function. In these functions, the independent variable is an exponent in the equation. The exponential function formula has the form y = abx. Because x is the exponent, if b is greater than 1, the output will grow very quickly for each small increase in the input value. Exponential functions are used for things involving rapid growth or decline like population growth and radioactive decay.
Here’s a table that shows x and y values for the equation y = 2x.
| x | y |
| -2 | 0.25 |
| -1 | 0.5 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
The graph of this function looks like this:
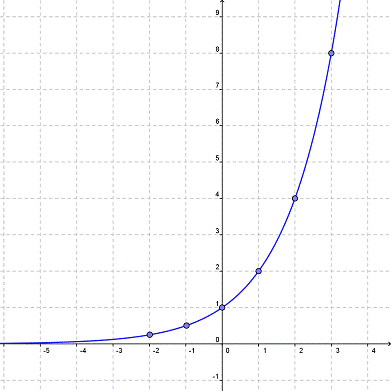
You can see why the mathematical term “exponential” has become a popular way to describe rapid, explosive change.
The letters a and b in the exponential function equation are coefficients that form the base of the exponent x. This interactive graph lets you manipulate these values on the graph of the equation y = abx. Click and drag the sliders labeled a and b and notice the large effect of small changes. In exponential functions, a little means a lot.
Summary
We’ve explored a few different kinds of nonlinear functions. Like linear functions, inverse relation, quadratic, and exponential functions can help us model real world situations and understand them better. Unlike linear functions, the rate of change in nonlinear functions is not constant but variable. Because of that, the graphs of nonlinear functions follow curved lines.