Fórmulas racionales y variación
Objetivos de aprendizaje
· Resolver una fórmula para una letra específica.
· Identificar variación directa, inversa y conjunta.
· Encontrar la incógnita en un problema de variación.
· Resolver problemas de aplicación que involucren variación directa.
· Resolver problemas de aplicación que involucren variación inversa.
· Resolver problemas de aplicación que involucren variación conjunta.
Introducción
Las fórmulas racionales pueden ser herramientas útiles para representar situaciones reales y para encontrar soluciones a problemas cotidianos. Las ecuaciones que representan variaciones, directas, inversas y conjuntas son ejemplos de fórmulas racionales que modelan situaciones del mundo real. Como puedes ver, si puedes encontrar una fórmula, normalmente puedes darle sentido a una situación
Cuando resolvemos problemas con fórmulas racionales, es útil despejar primero la fórmula para la variable específica. Por ejemplo, los problemas de trabajo piden calcular cuánto tiempo le toma a distintas personas trabajar a diferentes velocidades para realizar un trabajo. Los modelos algebraicos de dichas situaciones implican ecuaciones racionales derivadas de la fórmula del trabajo, W = rt. La cantidad de trabajo hecho (W) es el producto de la velocidad de trabajo (r) y el tiempo invertido en el trabajo (t). Usando álgebra, puedes escribir la fórmula del trabajo de tres maneras:
W = rt
Encontrar el tiempo (t): ![]() (dividir ambos lados entre r)
(dividir ambos lados entre r)
Encontrar la velocidad (r): ![]() (dividir ambos lados entre t)
(dividir ambos lados entre t)
| Ejemplo | |||||
| Problema | La fórmula para encontrar la densidad de un objeto es | ||||
|
|
|
| Empieza con la fórmula de la densidad. | ||
|
|
|
| Multiplica ambos lados de la ecuación por v para aislar m. | ||
|
|
|
| Simplifica y reescribe la ecuación, despejando m.
| ||
|
|
|
| Para resolver la ecuación | ||
| Respuesta |
|
|
| ||
Ahora veamos un ejemplo usando la fórmula del volumen de un cilindro.
| Ejemplo | |||||
| Problema | La fórmula para calcular el volumen de un cilindro es V = πr2h, donde V es el volumen, r es el radio y h es la altura del cilindro. Despeja la fórmula para resolver la altura (h). | ||||
|
|
|
| Empieza con la fórmula para el volumen de un cilindro.
| ||
|
|
|
| Divide ambos lados entre | ||
|
|
|
| Simplifica. Encuentras que la altura, h, es igual a | ||
| Respuesta |
|
|
| ||
Las ecuaciones de variación son ejemplos de fórmulas racionales y se usan para describir la relación entre variables. Por ejemplo, imagina un estacionamiento lleno de carros. El número total de llantas en el estacionamiento depende del número total de carros. Algebraicamente, puedes representar esta relación con una ecuación.
Número de carros = 4 • número de carros
El número 4 te dice la proporción de carros y llantas. Llamamos a esta proporción constante de variación. Es una constante porque este número no cambia. Ya que el número de carros y el número de llantas están ligados por una constante, un cambio en el número de carros causa un cambio proporcional en el número de llantas. Este es un ejemplo de variación directa, donde el número de llantas varía directamente con el número de carros.
Puedes usar la ecuación de carros y llantas como base para escribir ecuaciones algebraicas generales que sirvan para todos los ejemplos de variación directa. En el ejemplo, el número de llantas es la salida, 4 es la constante y el número de carros es la entrada. Pongamos estos términos genéricos en la ecuación. Obtienes salida = constante • entrada. Esa es la fórmula para todas las ecuaciones de variación directa..
Número de llantas = 4 • número de carros
salida = constante • entrada
Encontremos una forma general de representar una variación directa. Cuando hablamos de entrada y salida en una ecuación, normalmente podemos llamar esa ecuación una función. A la salida de la función (ecuación) también se le conoce como variable dependiente y generalmente es representada simbólicamente como y. La entrada se llama variable independiente, representada por el símbolo x. Representemos la constante con la letra k, Ahora pongamos esos símbolos en la ecuación.
Número de llantas = 4 • número de carros
salida = constante • entrada
y = kx
¡Y ya la tienes! Todas las ecuaciones de variación directa pueden describirse con la ecuación y = kx.
Veamos otro ejemplo de variación directa. Mary trabaja en un puesto junto a la granja de pollos de su familia, vende huevos por $1.99 por cartón en los fines de semana. Cuando los clientes compran muchos cartones a la vez, ella debe sumar los totales con papel y lápiz y le preocupa equivocarse. De suerte para Mary, esta es una relación de variación directa, la salida (costo total) es igual a la entrada (número de cartones) por una constante (el precio por cartón). Ella puede usar una ecuación de variación directa para hacer una tabla de precios y usarla como atajo.
En este caso, costo total = precio del cartón • número de cartones. Costo total = 1.99 • número de cartones.
| Número de cartones | Precio total |
| 1 | $1.99 |
| 2 | $3.98 |
| 3 | $5.97 |
| 4 | $7.96 |
| 5 | $9.95 |
| 6 | $11.94 |
Grafiquemos la función costo/cartón.
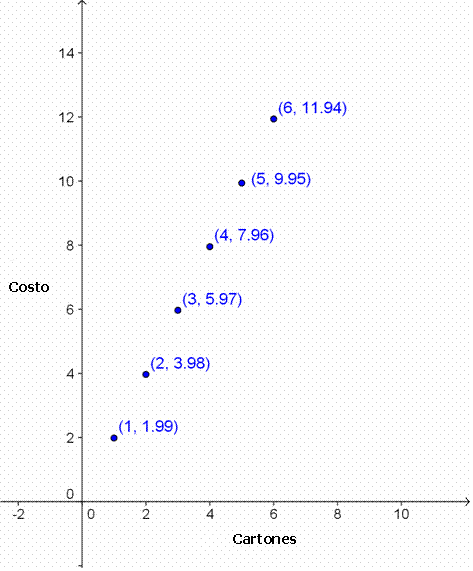
Esta función está hecha de puntos individuales porque el puesto sólo vende cartones individuales. Pero puedes ver que todos los puntos están espaciados uniformemente y parece que forman una recta. También puedes ver que si bien no está en la gráfica, el punto (0,0) satisface la función, el costo de 0 cartones sería de 0 dólares.
Ahora veamos la gráfica de la ecuación de variación directa y observar la diferencia con la gráfica anterior. (En la gráfica de la función continua, los puntos de datos individuales existen en cada punto sobre la recta, ¡a diferencia del ejemplo de los huevos donde no tiene sentido hablar del precio de 1.235 cartones de huevos!)
Imagina un grifo llena una bañera a un ritmo de 2.5 galones por minuto. La cantidad de agua en la bañera varía directamente con la cantidad de tiempo que el grifo permanece abierto. Puedes representar la relación entre el tiempo y el agua en la bañera con la siguiente fórmula.
Total de galones de agua = 2.5 galones de agua/minuto • tiempo en minutos
Usando g para representar el total de galones de agua y t para representar el tiempo, puedes abreviar esta relación como g = 2.5t, que se ve muy similar a la fórmula estándar para funciones proporcionales y = kx.
Hagamos una tabla para registrar la relación del tiempo contra la cantidad de agua en la bañera. Después de 1 minuto, hay 2.5 galones en la bañera. Después de 2 minutos, el total es de 5 galones, etc. Para encontrar la cantidad total de agua en la bañera en cualquier momento, puedes multiplicar el tiempo por 2.5 galones por minuto. Seis minutos deben darte suficientes puntos para hacer una gráfica útil.
| Tiempo | Galones totales |
| 1 | 2.5 |
| 2 | 5.0 |
| 3 | 7.5 |
| 4 | 10.0 |
| 5 | 12.5 |
| 6 | 15.0 |
Ahora puedes graficar los puntos.
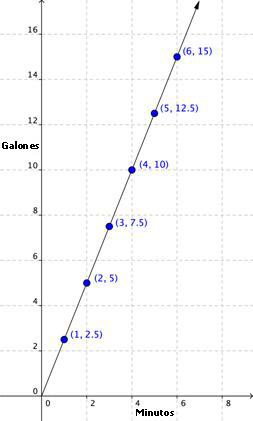
Esta vez, usa una recta para conectar los puntos, porque ambos el tiempo y el agua aumentan continuamente. Y observa, los puntos están en una recta que empieza en el origen y se eleva en un ángulo constante, justo como la gráfica anterior. En el ejemplo de los huevos, no tenía sentido comprar 2.5 cartones de huevos, por lo que no dibujabas una recta para conectar los puntos. Pero en el ejemplo del agua, puedes medir el número total de galones después de 2.5 minutos, por lo que conectar los puntos tiene sentido.
Cuando las variables en una función cambian a un ritmo constante, tienen una relación proporcional. Este ritmo continuo de cambio se llama constante de variación.
| Ejemplo | ||
| Problema | Resolver k, la constante de variación, en el problema de variación directa donde y = 300 y x = 10. | |
|
| y = kx | Escribe una fórmula para la relación de variación directa. |
|
| 300 = k(10) | Sustituye los valores conocidos en la ecuación. |
|
|
30 = k | Resuelve k dividiendo entre 10 ambos lados de la ecuación. |
| Respuesta | La constante de variación, k, es 30. |
|
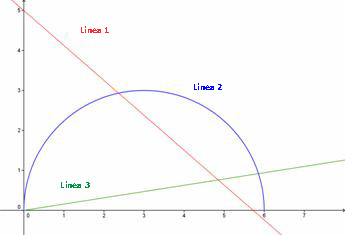
| ¿Qué recta en la gráfica siguiente muestra una variación directa?
A) Línea 1 B) Línea 2 C) Línea 3
|
Otro tipo de variación es la variación inversa. En estas ecuaciones, la variable dependiente es igual a la constante dividida entre la variable dependiente. En forma simbólica, esta es la ecuación ![]() , donde y es la variable dependiente, k es la constante y x es la variable dependiente. Compárala con la ecuación para una función que tiene una variación directa entre las variables, la fórmula de la variación directa es
, donde y es la variable dependiente, k es la constante y x es la variable dependiente. Compárala con la ecuación para una función que tiene una variación directa entre las variables, la fórmula de la variación directa es ![]() . La única diferencia es que la variable independiente está ahora en el denominador.
. La única diferencia es que la variable independiente está ahora en el denominador.
Un ejemplo de una variación inversa es la velocidad requerida para viajar entre dos ciudades en un tiempo dado.
Digamos que necesitas manejar desde Boston a Chicago, que está a unas 1,000 millas. Entre más tiempo tengas, más lento puedes ir. Si quieres llegar en 20 horas, necesitas viajar a 50 millas por hora (¡asumiendo que no te detienes!), porque ![]() . Pero si puedes tardar 40 horas en llegar, sólo tienes que viajar a un promedio de 25 millas por hora, porque
. Pero si puedes tardar 40 horas en llegar, sólo tienes que viajar a un promedio de 25 millas por hora, porque ![]() .
.
La ecuación para averiguar qué tan rápido viajas en cierto tiempo es ![]() . Esta ecuación debe recordarte que la fórmula de la distancia
. Esta ecuación debe recordarte que la fórmula de la distancia ![]() . Si resuelves
. Si resuelves ![]() para r obtienes
para r obtienes ![]() o
o ![]() .
.
En el caso del viaje de Boston a Chicago, puedes escribir ![]() . Observa que esta es la misma forma que la inversa de la fórmula de la función de variación,
. Observa que esta es la misma forma que la inversa de la fórmula de la función de variación, ![]() .
.
Aquí hay una tabla que muestra varios tiempos y varias velocidades que satisfacen la ecuación:
| Tiempo | Velocidad (millas por hora) |
| 1 | 1,000 |
| 5 | 200 |
| 10 | 100 |
| 12.5 | 80 |
| 20 | 50 |
| 25 | 40 |
| 40 | 25 |
Ahora, si graficas estos puntos, verás que la gráfica es definitivamente una curva, no una recta.
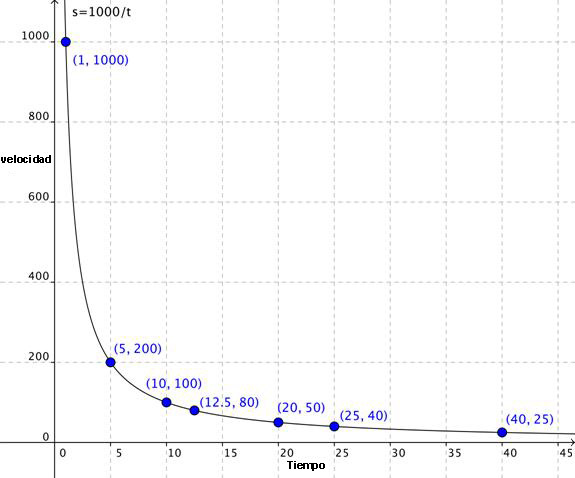
| Ejemplo | ||
| Problema | Resolver k, la constante de variación, en el problema de variación inversa donde x = 5 y y = 25. |
|
|
|
| Escribe una fórmula para la relación de variación directa. |
|
|
| Sustituye los valores conocidos en la ecuación. |
|
|
125 = k | Resuelve k multiplicando por 10 ambos lados de la ecuación. |
| Respuesta | La constante de variación, k, es 125. |
|
| Ejemplo | ||
| Problema | La temperatura del agua en el océano varía inversamente con la profundidad del agua. Entra más profundo, más fría se vuelve el agua. A una profundidad de 1,000 metros, la temperatura del agua es 5º Centígrados. ¿Cuál es la temperatura a una profundidad de 500 metros? | |
|
|
| Te dicen que es una relación inversa y que la temperatura del agua (y) varía inversamente con la profundidad del agua (x). |
|
|
| Sustituye los valores conocidos en la ecuación. |
|
|
| Resuelve k. |
|
|
| Ahora que conoces k, la constante de variación, usa la información para resolver el problema: encuentra la temperatura del agua a 500 metros. |
| Respuesta | A 500 metros, la temperatura del agua es 10º C. | |
| En una función de variación inversa, ¿qué le pasa a la salida cuando la entrada disminuye?
A) Aumenta. B) Disminuye.
|
Un tercer tipo de variación se llama variación conjunta. La variación conjunta es igual a la variación directa excepto porque hay dos o más cantidades. Por ejemplo, el área de un rectángulo puede encontrarse usando la fórmula A = lw, donde l es el largo del rectángulo y w es el ancho del rectángulo. Si cambias el ancho del rectángulo, entonces el área cambia y si cambias el largo del rectángulo entonces el área también cambia. Puedes decir que el área del rectángulo “varía conjuntamente con el largo y con el ancho del rectángulo.”
La fórmula para el volumen de un cilindro, ![]() es otro ejemplo de variación conjunta. El volumen del cilindro varía conjuntamente con el cuadrado del radio y la altura del cilindro. La constante de variación es
es otro ejemplo de variación conjunta. El volumen del cilindro varía conjuntamente con el cuadrado del radio y la altura del cilindro. La constante de variación es ![]() .
.
| Ejemplo | ||
| Problema | El área de un triángulo varía conjuntamente con la longitud de su base y de su altura. Si el área de un triángulo es de 30 pulgadas2 cuando la base es de 10 pulgadas y la altura es de 6 pulgadas, encuentra la constante de variación y el área de un triángulo cuya base es de 15 pulgadas y la altura es de 20 pulgadas. | |
|
| y = kxz
Área = k(base)(altura)
| Se te dice que esta es una relación de variación conjunta y el área de un triángulo (A) varía conjuntamente con la longitud de la base (b) y la longitud de la altura (h). |
|
| 30 = k(10)(6)
30 = 60k
| Sustituye valores conocidos en la ecuación y resuelve k. |
|
| Área = k(base)(altura)
Área = 150 pulgadas cuadradas | Ahora que conoces k, resuelve el área de un triángulo cuya base mide 15 pulgadas y cuya altura mide 20 pulgadas. |
| Respuesta | La constante de variación, k, es | |
Encontrar que k es ![]() no debería sorprendernos. Sabes que el área de un triángulo es un medio de la base por la altura,
no debería sorprendernos. Sabes que el área de un triángulo es un medio de la base por la altura, ![]() . ¡El
. ¡El ![]() en esta fórmula e exactamente el mismo
en esta fórmula e exactamente el mismo ![]() que calculaste en este ejemplo!
que calculaste en este ejemplo!
| Variación directa, inversa y conjunta
k es la constante de variación. En todos los casos, k ≠ 0.
|
Es importante ser capaz de distinguir si una aplicación varía directa, inversa o conjuntamente.
| Una roca que pesa 120 lb en la Tierra pesa 20 lb en la superficie de la Luna. De manera similar, un astronauta que pesa 240 lb en la Tierra pesará 40 lb en la Luna. ¿Es este un ejemplo de variación directa, inversa o conjunta?
A) Variación directa B) Variación inversa C) Variación conjunta
|
Sumario
Las fórmulas racionales pueden resolver una variedad de problemas que involucran ritmos, tiempos y trabajo. Las ecuaciones de variación directa, inversa y conjunta son ejemplos de fórmulas racionales. En la variación directa, las variables tienen una relación directa, conforme una cantidad aumenta, la otra cantidad también aumenta. Conforme una cantidad disminuye, la otra cantidad disminuye. En una variación inversa, las variables tienen una relación inversa, conforme una cantidad aumenta, la otra disminuye y vice versa. La variación conjunta es igual a la variación directa excepto que hay dos o más variables.