Resolviendo sistemas de tres variables
Objetivos de aprendizaje
· Resolver un sistema de ecuaciones cuando no es necesaria la multiplicación para eliminar una variable.
· Resolver un sistema de ecuaciones cuando es necesaria la multiplicación para eliminar una variable.
· Resolver problemas de aplicación que requieren el uso de este método.
· Reconocer sistemas que no tienen solución o que tienen un número infinito de soluciones.
Introducción
Las ecuaciones pueden tener más de una o dos variables. Te encontrarás con ecuaciones que tienen tres variables. Las ecuaciones con una variable se grafican en una recta. Las ecuaciones con dos variables se grafican en un plano. Las ecuaciones con tres variables se grafican en un espacio tridimensional.
Las ecuaciones con una variable requieren sólo una ecuación para tener una solución única. Las ecuaciones con dos variables requieren dos ecuaciones para tener una solución única (un par ordenado). Entonces no debería sorprendernos que las ecuaciones de tres variables requieren un sistema de tres ecuaciones para tener una solución única (una tercia ordenada).
Al igual que cuando resuelves sistemas de dos ecuaciones, hay tres posibles resultados para la solución de un sistema de tres variables. Estudiemos esto visualmente, aunque no graficaremos estas ecuaciones.
Caso 1: Existe una solución. Para que tres ecuaciones con tres variables tengan una solución, los planos deben interesectarse en un sólo punto.
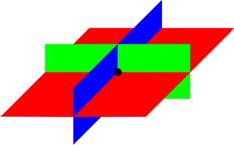
Caso 2: No hay solución. Los tres planos no tienen ningún punto en común. (Observa que dos ecuaciones podrían tener puntos en común una con la otra, pero no con las tres.) Abajo hay ejemplos de algunas maneras que esto sucede.



Caso 3: Existe un número infinito de soluciones. Esto ocurre cuando los tres planos se intersectan en una recta. Y también puede ocurrir cuando los tres planos están en el mismo plano.
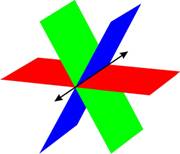

Empecemos con el Caso 1, donde el sistema tiene sólo una solución. Este es el caso en el que normalmente estamos interesados.
Aquí hay un sistema de ecuaciones lineales. Hay tres variables y tres ecuaciones.
| 3x | + | 4y | – | z | = | 8 |
| 5x | – | 2y | + | z | = | 4 |
| 2x | – | 2y | + | z | = | 1 |
Sabes cómo resolver un sistema con dos ecuaciones y dos variables. Para el primer paso, usa el método de eliminación para quitar una de las variables. En este caso, z puede ser eliminada sumando la primera ecuación con la segunda.
| 3x | + | 4y | – | z | = | 8 |
| 5x | – | 2y | + | z | = | 4 |
| 8x | + | 2y |
|
| = | 12 |
Para resolver el sistema, necesitas dos ecuaciones usando dos variables. Sumando la primera ecuación con la tercera en el sistema original también te dará una ecuación con x y y pero no con z.
| 3x | + | 4y | – | z | = | 8 |
| 2x | – | 2y | + | z | = | 1 |
| 5x | + | 2y |
|
| = | 9 |
Ahora tienes un sistema de dos ecuaciones con dos variables.
| 8x | + | 2y | = | 12 |
| 5x | + | 2y | = | 9 |
Resuelve el sistema de nuevo usando eliminación. En este caso, puedes eliminar y sumando el opuesto de la segunda ecuación:
|
| 8x | + | 2y | = | 12 |
|
|
| −5x | + | −2y | = | −9 |
|
|
| 3x |
|
| = | 3 |
|
Resuelve la ecuación resultante para la variable que queda.
| 3x = 3 |
| x = 1 |
Ahora usa una de las ecuaciones en el sistema de dos variables para encontrar y.
| 5x + 2y = 9 |
| 5(1) + 2y = 9 |
| 5 + 2y = 9 |
| 2y = 4 |
| y = 2 |
Finalmente, usa cualquier ecuación del primer sistema, junto con los valores que ya encontraste, para resolver la primera variable.
| 2x – 2y + z = 1 |
| 2(1) – 2(2) + z = 1 |
| 2 – 4 + z = 1 |
| −2 + z = 1 |
| z = 3 |
Asegúrate de comprobar tu respuesta. ¡Con tantos pasos, hay muchas posibilidades de cometer un error simple!
| 3x + 4y – z = 8 |
| 5x – 2y + z = 4 |
| 2x – 2y + z = 1 |
| 3(1) + 4(2) – 3 = 8 |
| 5(1) – 2(2) + 3 = 4 |
| 2(1) – 2(2) + 3 = 1 |
| 3 + 8 – 3 = 8 |
| 5 – 4 + 3 = 4 |
| 2 – 4 + 3 = 1 |
| 11 – 3 = 8 8 = 8 |
| 1 + 3 = 4 4 = 4 |
| −2 + 3 = 1 1=1 |
| VÁLIDO |
| VÁLIDO |
| VÁLIDO |
Como x = 1, y = 2, y z = 3 es una solución para las tres ecuaciones, es la solución del sistema de ecuaciones. Del mismo modo que dos valores se pueden escribir en un par ordenado, tres valores se pueden escribir en una tercia ordenada: (x, y, z) = (1, 2, 3).
| Resolviendo un sistema de tres variables 1. Escoge dos ecuaciones y úsalas para eliminar una variable. 2. Escoge otro par de ecuaciones y úsalas para eliminar la misma variable. 3. Usa el par resultante de ecuaciones para eliminar una de las otras variables. 4. Resuelve la ecuación final para la variable restante. 5. Encuentra el valor de la segunda variable. Usando una de las ecuaciones resultantes de los pasos 1 y 2 y el valor encontrado en el paso 4. 6. Encuentra el valor de la tercera variable. Usando una de las ecuaciones originales y los valores que encontraste en los pasos 4 y 5. 7. ¡Comprueba tu solución en las tres ecuaciones! |
| Ejemplo |
|
| ||||||||||||||||||||||
| Problema | Resolver f, g, y h. f + g + h = 13 f – h = −2 −2f + g = 3 |
| ||||||||||||||||||||||
|
|
| Paso 1: Escoge dos ecuaciones y elimina una variable. Las primeras dos ecuaciones pueden sumarse para eliminar h. | ||||||||||||||||||||||
|
| 2f + g = 11 −2f + g = 3 | Paso 2: ¡La tercera ecuación no tiene la variable h, por lo que no hay nada que eliminar! Tienes un sistema de dos ecuaciones con dos variables. | ||||||||||||||||||||||
|
|
| Paso 3: Elimina la segunda variable. Estas ecuaciones se pueden sumar para eliminar f. | ||||||||||||||||||||||
|
| 2g = 14 g = 7 | Paso 4: Resuelve la ecuación resultante para la variable faltante. | ||||||||||||||||||||||
|
| 2f + g = 11 2f + 7 = 11 2f = 4 f = 2 | Paso 5: Usa el valor y una de las ecuaciones del sistema en el paso 3 que tenga sólo 2 variables, una de las cuales es g que ya la conoces. Resuelve la segunda variable. | ||||||||||||||||||||||
|
| f + g + h = 13 2 + 7 + h = 13 9 + h = 13 h = 4 | Paso 6: Usa las dos variables ya encontradas y una de las ecuaciones originales que tenga las tres variables para encontrar la tercera variable. | ||||||||||||||||||||||
|
| f + g + h = 13 2 + 7 + 4 = 13 9 + 4 = 13 13 = 13 VÁLIDO
f – h = −2 2 – 4 = −2 −2= −2 VÁLIDO
−2f + g = 3 −2(2) + 7 = 3 −4 + 7 = 3 3 = 3 VÁLIDO | Paso 7: Comprueba tu respuesta. | ||||||||||||||||||||||
| Respuesta | La solución es (f, g, h) = (2, 7, 4). |
| ||||||||||||||||||||||
Del mismo modo que con los sistemas de dos variables, podrías necesitar sumar el opuesto de una de las ecuaciones o incluso multiplicar una de las ecuaciones antes de sumarlas para eliminar una variables.
| Ejemplo |
|
| |||||||||||||||||||||||||||||||||||||||||||||
| Problema | Resolver x, y, y z. 3x – 2y + z = 12 x + 3y + z = −4 2x + 2y – 4z = 6 |
| |||||||||||||||||||||||||||||||||||||||||||||
| Paso 1: Primero, escoge dos ecuaciones y elimina una variable. Multiplica la segunda ecuación por −1, y luego súmala con la primera ecuación. Esto eliminará z. | ||||||||||||||||||||||||||||||||||||||||||||||
| Paso 2: Luego, combina la tercera ecuación y una de las primeras dos para eliminar z de nuevo. Pero la tercera ecuación tiene un coeficiente de −4 en z mientras que los coeficientes en las primeras dos ecuaciones son 1. Entonces, multiplica la segunda ecuación pro 4 y suma. | ||||||||||||||||||||||||||||||||||||||||||||||
| Paso 3: Elimina la segunda variable usando las ecuaciones de los pasos 1 y 2. De nuevo, no pueden sumarse como están. Observa los coeficientes de x. Si multiplicas la ecuación del paso 1 por −3, los términos x tendrán el mismo coeficiente. | ||||||||||||||||||||||||||||||||||||||||||||||
| Multiplica y luego suma. ¡Ten cuidado con los signos! | ||||||||||||||||||||||||||||||||||||||||||||||
|
| 29y = −58 y = −2 | Paso 4: Resuelve la ecuación resultante para la variable faltante. | |||||||||||||||||||||||||||||||||||||||||||||
|
| 2x – 5y = 16 2x – 5(−2) = 16 2x + 10 = 16 2x = 6 x = 3 | Paso 5: Usa ese valor y una de las ecuaciones del paso 3, que tenga sólo dos variables, una que sea y. Resuelve para la segunda variable. | |||||||||||||||||||||||||||||||||||||||||||||
|
| x + 3y + z = −4 3 + 3(−2) + z = −4 3 + (−6) + z = −4 −3 + z = −4 z = −1 | Paso 6: Usa las dos variables encontradas y una de las ecuaciones originales para resolver la tercer variable. | |||||||||||||||||||||||||||||||||||||||||||||
|
| 3x – 2y + z = 12 3(3) – 2(−2) + (−1) = 12 9 + 4 – 1 = 12 13 – 1 = 12 12 = 12 VÁLIDO
x + 3y + z = −4 3 + 3(−2) + (−1) = −4 3 + (−6) + (−1) = −4 −3 + (−1) = −4 −4 = −4 VÁLIDO
2x + 2y – 4z = 6 2(3) + 2(−2) – 4(−1) = 6 6 + (−4) + 4 = 6 2 + 4 = 6 6 = 6 VÁLIDO | Paso 7: Comprueba tu respuesta. | |||||||||||||||||||||||||||||||||||||||||||||
| Respuesta | La solución es (x, y, z) = (3, −2, −1). |
| |||||||||||||||||||||||||||||||||||||||||||||
Estos sistemas pueden ser útiles para resolver problemas del mundo real.
| Ejemplo |
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Problema | Andrea vende fotografías en las ferias de arte. Los precios de sus fotos van de acuerdo con su tamaño: las fotos chicas cuestan $10, las fotos medianas cuestan $15, y las fotos grandes cuestan $40. Normalmente vende tantas fotos chicas como medianas y grandes combinadas. También vende el doble de fotos medianas que de fotos grandes. Un puesto en la ferie cuesta $300.
Si sus ventas son como normalmente, ¿cuántas fotos de cada tamaño necesita vender para pagar el puesto? |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| S = número de fotos pequeñas vendidas M = número de fotos medianas vendidas L = número de fotos grandes vendidas | Para crear el sistema, primero escoge las variables. En este caso los valores desconocidos son el número de fotos chicas, medianas y grandes. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 10S = dinero recibido por las fotos chicas 15M = dinero recibido por las fotos medianas 40L = dinero recibido por las fotos grandes
10S + 15M + 40L = 300 | El total de sus ventas debe ser $300 para pagar el puesto. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| S = M + L
M = 2L | El número de fotos chicas es el mismo que el total de fotos medianas y grandes.
Vende el doble de fotos medianas que de fotos grandes. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 10S + 15M + 40L = 300 S – M – L = 0 M – 2L = 0 | Para hacer las cosas más fáciles, reescribe las ecuaciones para que estén en el mismo formato, con todas las variables a la izquierda del signo igual y sólo un número constante a la derecha.
Ahora resuelve el sistema.
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Paso 1: Primero escoge dos ecuaciones y elimina una variable. Como una ecuación no tiene la variable S, puede ser útil usar las otras dos ecuaciones y eliminar la variable S.
Multiplica la segunda ecuación por −10 y suma. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| M – 2L = 0 | Paso 2: La segunda ecuación de nuestro sistema de dos variables será la ecuación restante (que no tiene la variable S). |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Paso 3: Elimina la segunda variable usando las ecuaciones de los pasos 1 y 2. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Si bien podrías multiplicar la segunda ecuación por 25 para eliminar L, los números se quedarán mejor si divides la primera ecuación entre 25. ¡No olvides tener cuidado con los signos! |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| 2M = 12 M = 6 | Paso 4: Resuelve la ecuación resultante para la variable que falta. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| M = 2L 6 = 2L 3 = L | Paso 5: Usa esa variable y una de las ecuaciones que contienen sólo dos variables, una de las variables que sea L que ya la conoces, para resolver la segunda variable.
Es mejor usar una de las ecuaciones originales — en caso de que hayas cometido un error en la multiplicación. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| S = M + L S = 6 + 3 S = 9 | Paso 6: Usa los dos valores y una de las ecuaciones originales para resolver la tercera variable
Incluso puedes usar una de las ecuaciones antes de escribirla para el sistema. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Normalmente vende tantas fotos chicas como medianas y grandes combinadas. Medianas y grandes combinadas = 6 + 3 = 9, que es la cantidad de fotos chicas.
También vende el doble de fotos medianas que de fotos grandes. Las fotos medianas son 6, lo que es el doble que las fotos grandes (3).
Un puesto en la feria cuesta $300. Andrea recibe $10(9) o $90 por las 9 fotos chicas, $15(6) o $90 por las 6 fotos medianas, y $40(3) o $120 por las fotos grandes. $90 + $90 + $120 = $300. | Paso 7: Comprueba tu respuesta. Con los problemas de aplicación, a veces es más fácil (y mejor) usar las instrucciones originales del problema en lugar de las ecuaciones que escribiste. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Respuesta | Si Andrea vende 9 fotos chicas, 6 fotos medianas, y 3 fotos grandes, recibirá exactamente la misma cantidad de dinero de lo que cuesta para pagar el puesto. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| En la solución de este sistema, ¿cuál es el valor de x? 7x − 4y + 3z = 28 3x + 3y – z = 19 3x + 2y + z = 16
A) 5
B) 16
C) -31
D) 1
|
Ahora veamos el Caso 2 (no hay solución) y el Caso 3 (hay un número infinito de soluciones).
Como no graficarás estas ecuaciones, porque es difícil graficar en tres dimensiones en una hoja de papel de 2 dimensiones, verás lo que pasa cuando intentas resolver sistemas sin solución o con un número infinito de soluciones.
Veamos un sistema que no tiene soluciones.
5x – 2y + z = 3
4x – 4y – 8z = 2
−x + y + 2z = −3
Supongamos que quieres resolver este sistema y empiezas con las dos últimas ecuaciones. Multiplica la última por 4 y suma para eliminar x.
| 4x | – | 4y | – | 8z | = | 2 |
| 4(−x | + | y | + | 2z) | = | 4(−3) |
|
|
|
|
|
|
|
|
| 4x | – | 4y | – | 8z | = | 2 |
| −4x | + | 4y | + | 8z | = | −12 |
|
|
|
|
| 0 | = | −10 |
En este caso, el resultado es un enunciado inválido. Esto significa que no hay soluciones para las dos ecuaciones y por lo tanto no puede haber soluciones para el sistema de tres ecuaciones. Si esto ocurre para cuales quiera dos de las tres ecuaciones, entonces no hay solución para el sistema de ecuaciones.
Ahora vemos un sistema que tiene un número infinito de soluciones.
x – 2y + z = 3
−3x + 6y – 3z = −9
4x – 8y + 4z = 12
Para el primer paso, escogerías dos ecuaciones y las combinarías para eliminar una variable. Puedes eliminar x multiplicando la primera ecuación por 3 y sumando la segunda ecuación.
| 3(x | – | 2y | + | z) | = | 3(3) |
| −3x | + | 6y | – | 3z | = | −9 |
|
|
|
|
|
|
|
|
| 3x | – | 6y | + | 3z | = | 9 |
| −3x | + | 6y | – | 3z | = | −9 |
|
|
|
|
| 0 | = | 0 |
Observa que cuando las dos ecuaciones se suman, ¡las variables se eliminan! La ecuación final es un enunciado válido: 0 = 0.
Cuando esto sucede, es porque las dos ecuaciones son equivalentes. Estas dos ecuaciones se graficarían en el mismo lugar. Pero para que la solución de un sistema de tres ecuaciones sea infinita, necesitas continuar con la tercera ecuación.
Como las primeras dos ecuaciones son equivalentes, el sistema de ecuaciones podría escribirse con sólo dos ecuaciones. Continúa como antes. Multiplica la primera ecuación por −4 y suma la tercera ecuación.
−4( x – 2y + z) =−4(3)
4x – 8y + 4z = −12
−4x + 8y – 4z = −12
4x – 8y + 4z = 12
0 = 0
Una vez más, la ecuación final es el enunciado válido 0 = 0. Por lo que la tercera ecuación está en el mismo plano que las primeras dos. Ahora puedes confirmar que hay un número infinito de soluciones — todos los puntos que están en el plano de estas tres ecuaciones son soluciones del sistema.
Este es un tipo de situación donde hay un número infinito de soluciones. Existen otros, que no examinaremos esta vez.
| Ejemplo | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Problema | ¿Cuántas soluciones tiene el siguiente sistema de ecuaciones?
x + y + z = 2 2x + 2y + 2z = 4 −3x – 3y – 3z = −6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Multiplica la primera ecuación por −2 y luego suma la ecuación resultante a la segunda ecuación.
0 = 0 es un enunciado válido, que nos hace pensar que podríamos tener un número infinito de soluciones. Este resultado indica que el primer par de ecuaciones es realmente la misma ecuación. Los valores de x, y, y z que funcionarían en la primera ecuación también lo harían en la segunda. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Ahora suma la tercera ecuación con la primera.
De nuevo, el resultado es otro enunciado válido. La primera ecuación y la tercera son las mismas. Por lo que tienes tres ecuaciones que se graficarán en el mismo plano. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Respuesta | Existe un número infinito de soluciones para este sistema. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ejemplo | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Problema | Resolver el siguiente sistema de ecuaciones. x – y – 2z = 4 4x – 4y – z = 2 −x + y + 2z = −3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
| Compara los coeficientes en los términos x. Multiplica la primera ecuación por −4 y luego suma la ecuación resultante a la segunda ecuación.
Observa que se produce un enunciado inválido: 0 = −14. Esto significa que no hay solución para este sistema de ecuaciones; no es necesario que continúes tratando de resolverlo. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Respuesta | El sistema no tiene soluciones. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ¿Cuántas soluciones tiene este sistema? 6x + 4y + 2z = 32 3x – 3y – z = 19 3x + 2y + z = 32
A) No tiene soluciones
B) Una
C) Un número infinito de soluciones
|
Sumario
Combinar ecuaciones es una herramienta útil para resolver sistemas de ecuaciones, incluidos los sistemas con tres ecuaciones y tres variables. Algunas veces, debes multiplicar una de las ecuaciones antes de sumarla para que puedas eliminar una variable. Continúas con el proceso de combinar ecuaciones y eliminar variables hasta que hayas encontrado todos los valores de todas las variables. Ocasionalmente este proceso lleva a que todas las variables sean eliminadas (eliminadas, no resueltas). Cuando todas las variables son eliminadas debido a las combinaciones de ecuaciones, si nos lleva a un enunciado inválido, entonces el sistema no tiene soluciones. Cuando todas las variables han sido eliminadas por las combinaciones de ecuaciones, si una de las ecuaciones resultantes es válida, entonces el sistema podría tener un número infinito de soluciones. Sin embargo, todas las ecuaciones deben ser comparadas y deben encontrarse enunciados válidos para que tengan un número infinito de soluciones, no sólo dos de las tres ecuaciones.
