Understanding Exponents and Square Roots
Learning Objective(s)
· Evaluate expressions containing exponents.
· Write repeated factors using exponential notation.
· Find a square root of a perfect square.
Introduction
Exponents provide a special way of writing repeated multiplication. Numbers written in this way have a specific form, with each part providing important information about the number. Writing numbers using exponents can save a lot of space, too. The inverse operation of multiplication of a number by itself is called finding the square root of a number. This operation is helpful for problems about the area of a square.
Exponential notation is a special way of writing repeated factors, for example 7 • 7. Exponential notation has two parts. One part of the notation is called the base. The base is the number that is being multiplied by itself. The other part of the notation is the exponent, or power. This is the small number written up high to the right of the base. The exponent, or power, tells how many times to use the base as a factor in the multiplication. In the example, 7 • 7 can be written as 72, 7 is the base and 2 is the exponent. The exponent 2 means there are two factors.
72 = 7 • 7 = 49
You can read 72 as “seven squared.” This is because multiplying a number by itself is called “squaring a number.” Similarly, raising a number to a power of 3 is called “cubing the number.” You can read 73 as “seven cubed.”
You can read 25 as “two to the fifth power” or “two to the power of five.” Read 84 as “eight to the fourth power” or “eight to the power of four.” This format can be used to read any number written in exponential notation. In fact, while 63 is most commonly read “six cubed,” it can also be read “six to the third power” or “six to the power of three.”
To find the value of a number written in exponential form, rewrite the number as repeated multiplication and perform the multiplication. Two examples are shown below.
| Example | ||||
| Problem | Find the value of 42. |
|
| |
|
| 4 is the base. 2 is the exponent. | An exponent means repeated multiplication.
The base is 4; 4 is the number being multiplied.
The exponent is 2; This means to use two factors of 4 in the multiplication. |
| |
|
| 42 = 4 • 4 | Rewrite as repeated multiplication. |
| |
|
| 4 • 4 = 16 | Multiply.
|
| |
| Answer 42 = 16 | ||||
| Example | ||||
| Problem | Find the value of 25. |
|
| |
|
| 2 • 2 • 2 • 2 • 2 | Rewrite 25 as repeated multiplication. The base is 2, the number being multiplied. The exponent is 5, the number of times to use 2 in the multiplication.
|
| |
|
| 2 • 2 • 2 • 2 • 2 4 • 2 • 2 • 2 8 • 2 • 2 16 • 2 32 | Perform multiplication.
|
| |
| Answer 25 = 32 | ||||
| Find the value of 43.
A) 12
B) 64
C) 256
D) 43
|
Writing repeated multiplication in exponential notation can save time and space. Consider the example 5 • 5 • 5 • 5. We can use exponential notation to write this repeated multiplication as 54. Since 5 is being multiplied, it is written as the base. Since the base is used 4 times in the multiplication, the exponent is 4. The expression 5 • 5 • 5 • 5 can be rewritten in shorthand exponential notation as 54 and is read, “five to the fourth power” or “five to the power of 4.”
To write repeated multiplication of the same number in exponential notation, first write the number being multiplied as the base. Then count how many times that number is used in the multiplication, and write that number as the exponent. Be sure to count the numbers, not the multiplication signs, to determine the exponent.
| Example | ||||
| Problem | Write 7 • 7 • 7 in exponential notation. |
|
| |
|
| 7 is the base.
Since 7 is used 3 times, 3 is the exponent. | The base is the number being multiplied, 7.
The exponent tells the number of times the base is multiplied. |
| |
Answer 7 • 7 • 7 = 73 This is read “seven cubed.” | ||||
|
Write 10 • 10 • 10 • 10 • 10 • 10 in exponential notation.
A) 1,000,000
B) 60
C) 105
D) 106
|
As you saw earlier, 52 is called “five squared.” “Five squared” means to multiply five by itself. In mathematics, we call multiplying a number by itself “squaring” the number. We call the result of squaring a whole number a square or a perfect square. A perfect square is any number that can be written as a whole number raised to the power of 2. For example, 9 is a perfect square. A perfect square number can be represented as a square shape, as shown below. We see that 1, 4, 9, 16, 25, and 36 are examples of perfect squares.
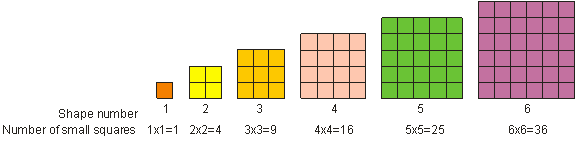

To square a number, multiply the number by itself. 3 squared = 32 = 3 • 3 = 9.
Below are some more examples of perfect squares.
| 1 squared | 12 | 1 • 1 | 1 |
| 2 squared | 22 | 2 • 2 | 4 |
| 3 squared | 32 | 3 • 3 | 9 |
| 4 squared | 42 | 4 • 4 | 16 |
| 5 squared | 52 | 5 • 5 | 25 |
| 6 squared | 62 | 6 • 6 | 36 |
| 7 squared | 72 | 7 • 7 | 49 |
| 8 squared | 82 | 8 • 8 | 64 |
| 9 squared | 92 | 9 • 9 | 81 |
| 10 squared | 102 | 10 • 10 | 100 |
The inverse operation of squaring a number is called finding the square root of a number. Finding a square root is like asking, “what number multiplied by itself will give me this number?” The square root of 25 is 5, because 5 multiplied by itself is equal to 25. Square roots are written with the mathematical symbol, called a radical sign, that looks like this: ![]() . The “square root of 25” is written
. The “square root of 25” is written ![]() .
.
| Example | ||||
| Problem | Find |
|
| |
|
|
| Think, what number times itself gives 81? 9 • 9 = 81
|
| |
| Answer |
|
|
| |
| Find
A) 6
B) 18
C) 72
D) 7
|
Summary
Exponential notation is a shorthand way of writing repeated multiplication of the same number. A number written in exponential notation has a base and an exponent, and each of these parts provides information for finding the value of the expression. The base tells what number is being repeatedly multiplied, and the exponent tells how many times the base is used in the multiplication. Exponents 2 and 3 have special names. Raising a base to a power of 2 is called “squaring” a number. Raising a base to a power of 3 is called “cubing” a number. The inverse of squaring a number is finding the square root of a number. To find the square root of a number, ask yourself, “What number can I multiply by itself to get this number?”
