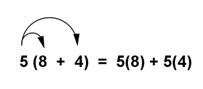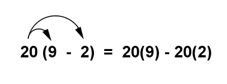The Distributive Property
Learning Objective(s)
· Simplify using the distributive property of multiplication over addition.
· Simplify using the distributive property of multiplication over subtraction.
Introduction
The distributive property of multiplication is a very useful property that lets you simplify expressions in which you are multiplying a number by a sum or difference. The property states that the product of a sum or difference, such as 6(5 – 2), is equal to the sum or difference of the products – in this case, 6(5) – 6(2).
Remember that there are several ways to write multiplication. 3 x 6 = 3(6) = 3 • 6.
3 • (2 + 4) = 3 • 6 = 18.
The distributive property of multiplication over addition can be used when you multiply a number by a sum. For example, suppose you want to multiply 3 by the sum of 10 + 2.
3(10 + 2) = ?
According to this property, you can add the numbers and then multiply by 3.
3(10 + 2) = 3(12) = 36. Or, you can first multiply each addend by the 3. (This is called distributing the 3.) Then, you can add the products.
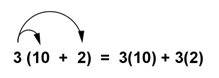
The multiplication of 3(10) and 3(2) will each be done before you add.
3(10) + 3(2) = 30 + 6 = 36. Note that the answer is the same as before.
You probably use this property without knowing that you are using it. When a group (let’s say 5 of you) order food, and order the same thing (let’s say you each order a hamburger for $3 each and a coke for $1 each), you can compute the bill (without tax) in two ways. You can figure out how much each of you needs to pay and multiply the sum times the number of you. So, you each pay (3 + 1) and then multiply times 5. That’s 5(3 + 1) = 5(4) = 20. Or, you can figure out how much the 5 hamburgers will cost and the 5 cokes and then find the total. That’s 5(3) + 5(1) = 15 + 5 = 20. Either way, the answer is the same, $20.
The two methods are represented by the equations below. On the left side, we add 10 and 2, and then multiply by 3. The expression is rewritten using the distributive property on the right side, where we distribute the 3, then multiply each by 3 and add the results. Notice that the result is the same in each case.
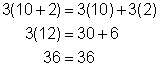
The same process works if the 3 is on the other side of the parentheses, as in the example below.
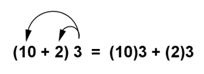
| Example | ||
| Problem | Rewrite the expression 5(8 + 4) using the distributive property of multiplication over addition. Then simplify the result. | |
|
40 + 20 = 60 |
In the original expression, the 8 and the 4 are grouped in parentheses. Using arrows, you can see how the 5 is distributed to each addend. The 8 and 4 are each multiplied by 5.
The resulting products are added together, resulting in a sum of 60. | |
|
Answer 5(8 + 4) = 5(8) + 5(4) = 60 | ||
| Rewrite the expression 30(2 + 4) using the distributive property of addition.
A) 30(2 + 4) + 30(2 + 4)
B) 30(2) + 30(4)
C) 30(6)
D) 30(24)
|
The distributive property of multiplication over subtraction is like the distributive property of multiplication over addition. You can subtract the numbers and then multiply, or you can multiply and then subtract as shown below. This is called “distributing the multiplier.”
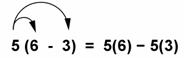
The same number works if the 5 is on the other side of the parentheses, as in the example below.
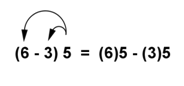
In both cases, you can then simplify the distributed expression to arrive at your answer. The example below, in which 5 is the outside multiplier, demonstrates that this is true. The expression on the right, which is simplified using the distributive property, is shown to be equal to 15, which is the resulting value on the left as well.
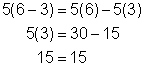
| Example | ||
| Problem | Rewrite the expression 20(9 – 2) using the distributive property of multiplication over subtraction. Then simplify. | |
|
180 – 40 = 140 |
In the original expression, the 9 and the 2 are grouped in parentheses. Using arrows, you can see how the 20 is distributed to each number so that the 9 and 2 are both multiplied by 20 individually.
Here, the resulting product of 40 is subtracted from the product of 180, resulting in an answer of 140. | |
|
Answer 20(9 – 2) = 20(9) – 20(2) = 140 | ||
|
Rewrite the expression 10(15 – 6) using the distributive property of subtraction.
A) 10(6) – 10(15)
B) 10(9)
C) 10(6 –15)
D) 10(15) – 10(6)
|
Summary
The distributive properties of addition and subtraction can be used to rewrite expressions for a variety of purposes. When you are multiplying a number by a sum, you can add and then multiply. You can also multiply each addend first and then add the products. This can be done with subtraction as well, multiplying each number in the difference before subtracting. In each case, you are distributing the outside multiplier to each number in the parentheses, so that multiplication occurs with each number before addition or subtraction occurs. The distributive property will be useful in future math courses, so understanding it now will help you build a solid math foundation.