Place Value and Names for Whole Numbers
Learning Objective(s)
· Find the place value of a digit in a whole number.
· Write a whole number in words and in standard form.
· Write a whole number in expanded form.
Introduction
Mathematics involves solving problems that involve numbers. We will work with whole numbers, which are any of the numbers 0, 1, 2, 3, and so on. We first need to have a thorough understanding of the number system we use. Suppose the scientists preparing a lunar command module know it has to travel 382,564 kilometers to get to the moon. How well would they do if they didn’t understand this number? Would it make more of a difference if the 8 was off by 1 or if the 4 was off by 1?
In this section, you will take a look at digits and place value. You will also learn how to write whole numbers in words, standard form, and expanded form based on the place values of their digits.
A digit is one of the symbols 0, 1, 2, 3, 4, 5, 6, 7, 8, or 9. All numbers are made up of one or more digits. Numbers such as 2 have one digit, whereas numbers such as 89 have two digits. To understand what a number really means, you need to understand what the digits represent in a given number.
The position of each digit in a number tells its value, or place value. We can use a place-value chart like the one below to easily see the place value for each digit. The place values for the digits in 1,456 are shown in this chart.
| Place-Value Chart | ||||||||||||||
| Trillions | Billions | Millions | Thousands | Ones | ||||||||||
|
|
|
|
|
|
|
|
|
|
|
| 1 | 4 | 5 | 6 |
| Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones |
In the number 1,456, the digit 1 is in the thousands place. The digit 4 is in the hundreds place. The digit 5 is in the tens place, and the digit 6 is in the ones place.
As you see above, you can tell a digit’s value by looking at its position. Look at the number of digits to the right of the digit, or write your number into a place-value chart, with the last digit in the ones column. Both these methods are shown in the example below.
| Example | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Problem | The development of a city over the past twenty years cost $962,234,532,274,312. What is the value of the digit 6 in this number? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Write the number in the place-value chart. Read the value of the 6 from the chart. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
$962,234,532,274,312 60,000,000,000,000 |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Answer The value of the digit 6 is 60 trillion. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| In a far away galaxy, there are 2,968,351,472 stars. What does the digit 3 represent in this problem?
A) three hundred thousands
B) three hundreds
C) three hundred trillions
D) three hundred millions
|
The standard form of a number refers to a type of notation in which digits are separated into groups of three by commas. These groups of three digits are known as periods. For example, 893,450,243 has three periods with three digits in each period, as shown below.
| Place-Value Chart | ||||||||||||||
| Trillions | Billions | Millions | Thousands | Ones | ||||||||||
|
|
|
|
|
|
| 8 | 9 | 3 | 4 | 5 | 0 | 2 | 4 | 3 |
| Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones |
Let’s examine the number of digits and periods in a greater number. The number of body cells in an average adult human is about one hundred trillion. This number is written as 100,000,000,000,000. Notice that there are 15 digits and 5 periods. Here is how the number would look in a place-value chart.
| Place-Value Chart | ||||||||||||||
| Trillions | Billions | Millions | Thousands | Ones | ||||||||||
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones |
You are now familiar with the place values of greater numbers, so let’s examine a problem that involves converting from standard form to a word name.
Converting Standard Form to Word Names
We often use word names to write numbers. A word name for 42 is “forty-two.” The total number of weeks in a year, 52, is written as “fifty-two.”
For whole numbers with three digits, use the word “hundred” to describe how many hundreds there are in the number. For example, for the number of days in a normal year, 365, the digit 3 is in the hundreds place. The word name for the number is “three hundred sixty-five.”
For whole numbers with four digits, begin the name with the number of thousands, followed by the period name, as in the example below.
| Example | ||
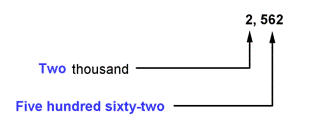
| Problem | A man owes $2,562 on a car. Write the word name for this. | |
|
| ||
| Answer | The word name is two thousand, five hundred sixty-two. | |
For word names of greater numbers, begin at the left with the greatest period. For each period, write the one- to three-digit number in the period, and then the period name. See the example below.
| Example | ||
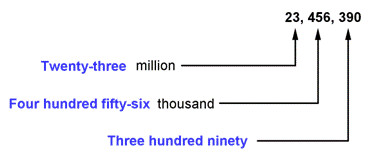
| Problem | The construction of a new athletic center cost $23,456,390. Write the word name for this number. | |
|
| ||
| Answer | The word name is twenty-three million, four hundred fifty-six thousand, three hundred ninety. | |
Converting Word Names to Standard Form
When converting word names to standard form, the word “thousand” tells you which period the digits are in. See the example below.
| Example | ||||||||||||||||
| Problem | Forty-seven thousand, five hundred eighty-six blueberries are produced on a farm over the course of three years. Write this number in standard form. | |||||||||||||||
|
Forty-seven thousand
Five hundred eighty-six
Standard Notation is 47,586
| ||||||||||||||||
| Answer | The number in standard form is 47,586. | |||||||||||||||
Below is an example with a number containing more digits. The words “million” and “thousand” tell you which periods the digits are in. The periods are separated by commas.
| Example | ||
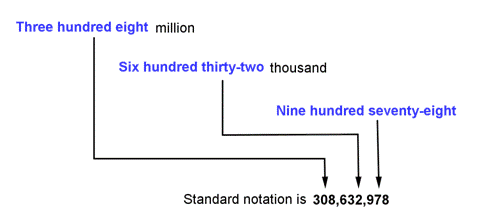
| Problem | There are three hundred eight million, six hundred thirty-two thousand, nine hundred seventy-eight bacteria in a sample of soil. Write this number in standard form. | |
|
| ||
| Answer | The number in standard form is 308,632,978. | |
Some numbers in word form may not mention a specific period. For example, three million, one hundred twelve written in standard form is 3,000,112. Because the thousands period is not mentioned, you would write three zeros in the thousands period. You can use a place-value chart to make it easier to see the values of the digits. See the example below.
| Example |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
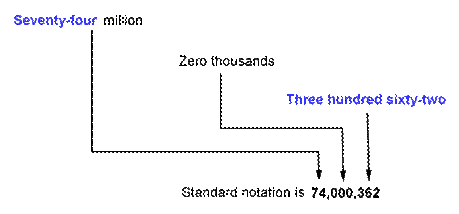
| Problem | A company had a new office building constructed. The final cost was seventy-four million, three hundred sixty-two dollars. Write this number in standard form. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Placing this number in a place- value chart shows that the thousands period is zero.
Remember to separate each period with a comma. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Answer The number written in standard form is $74,000,362. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sometimes it is useful to write numbers in expanded form. In expanded form, the number is written as a sum of the value of each digit.
| Example | ||||
| Problem | During the week, Mike drives a total of 264 miles. Write 264 in expanded form. | |||
| First, identify the value of each digit.
In numerical form: | ||||
| 264 | 200 | |||
| 264 | 60 | |||
| 264 | 4 | |||
| In word form: |
| |||
| 264 | 2 hundreds | |||
| 264 | 6 tens | |||
| 264 | 4 ones | |||
| Then, write the numbers as a sum. | ||||
| Answer | 264 written in expanded form is
200 + 60 + 4, or
2 hundreds + 6 tens + 4 ones, or
(2 • 100) + (6 • 10) + (4 • 1) | |||
You can also use a place-value chart to help write a number in expanded form. Suppose the number of cars and pick-up trucks in the U.S. at this very moment is 251,834,697. Place this number in a place-value chart.
| Place-Value Chart | ||||||||||||||
| Trillions | Billions | Millions | Thousands | Ones | ||||||||||
|
|
|
|
|
|
| 2 | 5 | 1 | 8 | 3 | 4 | 6 | 9 | 7 |
| Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones | Hundreds | Tens | Ones |
| 2 hundred millions | 200,000,000 |
| + 5 ten millions | +50,000,000 |
| + 1 million | +1,000,000 |
| + 8 hundred thousands | +800,000 |
| + 3 ten thousands | +30,000 |
| + 4 thousands | +4,000 |
| + 6 hundreds | +600 |
| + 9 tens | +90 |
| + 7 ones | +7 |
Summary
Whole numbers that are greater than 9 consist of multiple digits. Each digit in a given number has a place value. To better understand place value, numbers can be put in a place-value chart so that the value of each digit can be identified. Numbers with more than three digits can be separated into groups of three digits, known as periods. Any whole number can be expressed in standard form, expanded form, or as a word name.