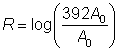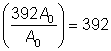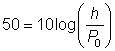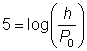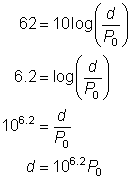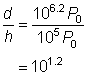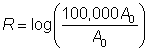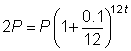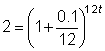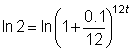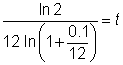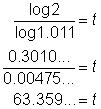Mathematical Modeling with Exponential and Logarithmic Functions
Learning Objective(s)
· Solve applied problems involving logarithmic functions.
· Solve applied problems involving exponential functions.
Introduction
You have seen many different kind of functions. You know that each one can be used to model some kind of situation in the real world. Exponential and logarithmic functions are no exception!
Much of the power of logarithms is their usefulness in solving exponential equations. Some examples of this include sound (decibel measures), earthquakes (Richter scale), the brightness of stars, and chemistry (pH balance, a measure of acidity and alkalinity).
Let’s look at the Richter scale, a logarithmic function that is used to measure the magnitude of earthquakes. The magnitude of an earthquake is related to how much energy is released by the quake. Instruments called seismographs detect movement in the earth; the smallest movement that can be detected shows on a seismograph as a wave with amplitude A0.
A – the measure of the amplitude of the earthquake wave
A0 – the amplitude of the smallest detectable wave (or standard wave)
From this you can find R, the Richter scale measure of the magnitude of the earthquake using the formula:
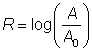
The intensity of an earthquake will typically measure between 2 and 10 on the Richter scale. Any earthquakes registering below a 5 are fairly minor; they may shake the ground a bit, but are seldom strong enough to cause much damage. Earthquakes with a Richter rating of between 5 and 7.9 are much more severe, and any quake above an 8 is likely to cause massive damage. (The highest rating ever recorded for an earthquake is 9.5 during the 1960 Valdivia earthquake in Chile.)
| Example | ||
| Problem | An earthquake is measured with a wave amplitude 392 times as great as A0. What is the magnitude of this earthquake using the Richter scale, to the nearest tenth? | |
|
|
| Use the Richter scale equation.
Since A is 392 times as large as A0, A = 392A0. Substitute this expression in for A.
|
|
|
R = log 392 R = 2.5932… R | Simplify the expression
Use a calculator to evaluate the logarithm. |
| Answer | The magnitude of this earthquake is 2.6 on the Richter scale. | |
A difference of 1 point on the Richter scale equates to a 10-fold difference in the amplitude of the earthquake (which is related to the wave strength). This means that an earthquake that measures 3.6 on the Richter scale has 10 times the amplitude of one that measures 2.6.
Let’s look back at the example just shown. In that example, the wave amplitude of the earthquake was 392 times normal. What if it were 10 times that, or 3,920 times normal? To find the measurement of that size earthquake on the Richter scale, you find log 3920. A calculator gives a value of 3.5932…or 3.6, when rounded to the nearest tenth. One extra point on the Richter scale can mean a lot more shaking!
Sound is measured in a logarithmic scale using a unit called a decibel. The formula looks similar to the Richter scale:
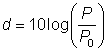
where P is the power or intensity of the sound and P0 is the weakest sound that the human ear can hear.
| Example | ||
| Problem | One hot water pump has a noise rating of 50 decibels. One dishwasher, however, has a noise rating of 62 decibels. The dishwasher noise is how many times more intense than the hot water pump noise? | |
|
|
| You can’t easily compare the two noises using the formula, but you can compare them to P0. Start by finding the intensity of noise for the hot water pump. Use h for the intensity of the hot water pump’s noise. |
|
|
| Divide the equations by 10 to get the log by itself. |
|
|
| Rewrite the equation as an exponential equation. |
|
| h = 105P0
| Multiply by P0 to get h by itself. |
|
|
| Repeat the same process to find the intensity of the noise for the dishwasher. |
|
|
| To compare d to h, you can divide. (Think: if the dishwasher’s noise is twice as intense as the pump’s, then d should be 2h—that is, Use the laws of exponents to simplify the quotient.
|
| Answer | The dishwasher’s noise is 101.2 (or about 15.85) times as intense as the hot water pump. | |
With decibels, every increase of 10 means the sound is 10 times more intense. An increase of 20 would be 10 times more intense for the first 10, and another 10 times more intense for the second 10—so a sound that is 75 decibels is 100 times more intense than a sound that is 55 decibels!
Here’s one more example of logarithms used in scientific contexts. The measure of acidity of a liquid is called the pH of the liquid. This is based on the amount of hydrogen ions (H+) in the liquid. The formula for pH is:
pH = −log[H+]
where [H+] is the concentration of hydrogen ions, given in a unit called mol/L (“moles per liter”; one mole is 6.022 x 1023 molecules or atoms).
Liquids with a low pH (down to 0) are more acidic than those with a high pH. Water, which is neutral (neither acidic nor alkaline, the opposite of acidic) has a pH of 7.0.
| Example | ||
| Problem | If lime juice has a pH of 1.7, what is the concentration of hydrogen ions (in mol/L) in lime juice, to the nearest hundredth? | |
|
| pH = −log[H+] | Use the formula for pH. |
|
| 1.7 = −log x | Substitute the known pH into the formula, and represent H+ with the variable x. |
|
| −1.7 = log x | If 1.7 = −log x, then log x = −1.7. |
|
| x = 10-1.7 x = 0.02. | Solve for x.
|
| Answer | The concentration of hydrogen ions in lime juice is 0.02. | |
| An earthquake monitoring station measured the amplitude of the waves during a recent tremor. It measured the waves as being 100,000 times as large as A0, the smallest detectable wave. How high did this earthquake measure on the Richter scale?
A) 1 B) 3 C) 5 D) 9
|
Exponential functions are used for even more contexts, including population and bacterial growth, radioactive decay, compound interest, cooling of objects, and growth of phenomena such as virus infections, Internet usage, and popularity of fads.
For example, recall that the formula for compound interest is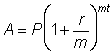 
, where P is principal, A is amount, r is the annual rate, m is the number of compounding periods, and t is the number of years.
| Example | ||
| Problem | How long will it take, to the nearest whole year, for money to double if it is invested at 10% compounded monthly? | |
|
| P = initial investment A = 2P (since you want the money to double) r = 0.1 (10% written as a decimal) m = 12 (12 compound periods per year) t is the value you are looking for. | Find values for the variables that you can. Note that you don’t know either P or A, but you know the relationship between P and A. |
|
|
| Use the formula. |
|
|
| Divide both sides by P to get the exponential expression by itself. Note: This means P can’t be 0, since you can’t divide by 0. But if P were 0, no money would actually be invested and the problem wouldn’t make sense anyway. So it’s fine to assume P > 0. |
|
|
| To solve an equation with the variable in the exponent, take logarithms of both sides. You can use any base, so log (base 10) or ln (base e) would be best, then you can use a calculator to evaluate the logarithms. |
|
|
| Use the power property of logarithms to get the variable out of the exponent. |
|
|
| Divide to get t by itself. |
|
|
| Use the calculator to evaluate the logarithms. |
| Answer | The money will double in about 7 years. | Round to the nearest whole year. |
According to the U.S. Census Bureau, the world population in 2011 was about 6.9 billion people, and would grow about 76 million during the year. That is, it would increase about 1.1%.
If the world population grows by 1.1% every year, then each year the population is multiplied by 1.011. (The 1 represents the current population, and the .011 represents the new growth.) After two years, the population would be 6.9(1.011)2, and after three years it would be 6.9(1.011)3. In general, the world population P (in billions of people) could be estimated for t years after 2011 by this formula:
P = 6.9(1.011)t
| Example | ||
| Problem | Using the world population formula P = 6.9(1.011)t, where t is the number of years after 2011 and P is the world population in billions of people, estimate: a) the population in the year 2050 to the nearest hundred million, and b) by what year will the population be double what it was in 2011. | |
|
| Part a t = 2050 – 2011 = 39 P is what you are looking for. | Looking at part a first, identify the variables. In this case, 2050 is 39 years after 2011, so t = 39. |
|
| P = 6.9(1.011)39 P = 10.57… P ≈ 10.6 | Use the formula and a calculator to evaluate the exponential expression. (Note that “hundred million” is a tenth of a billion, so to the nearest hundred million is 10.6.) According to the problem, the formula finds P in billions of people, so you have 10.6 billion people. |
|
| Part b t is what you are looking for. P = 2(6.9) = 13.8 | For part b, you want the population to double the 6.9 from 2011, so P = 13.8. |
|
| 13.8 = 6.9(1.011)t | Use the formula and the value for P. |
|
| 2 = 1.011t | Divide by 6.9 to get the exponential expression by itself. |
|
| log 2 = log(1.011)t | Since the variable t is an exponent, take logarithms of both sides. You can use any base, but base 10 or e will allow you to use the calculator easily. |
|
| log 2 = t log 1.011
| Use the power property of logarithms to get the variable out of the exponent, and then solve for t. The population will hit the doubling point about halfway through the 63rd year, so you will round up to 64 (since the question asks by what year). |
|
| 2011 + 64 = 2075 | It will take about 64 years for the population to double, so you have to add 64 to 2011 to estimate the year the world population will be 13.8 billion people. |
| Answer | a) The population in 2050 will be about 10.6 billion people. b) The population will double (13.8 billion people) the 2011 population by the year 2075. | Be sure to answer the questions asked. |
| A particular bacterial colony doubles its population every 15 hours. A scientist running an experiment is starting with 100 bacteria cells. She expects the number of cells to be given by the formula
After how many hours would the scientist expect to have 300 bacteria cells? Give your answer to the nearest hour.
A) 2 hours B) 24 hours C) 1,048,577 hours D) 104,857,699 hours
|
Summary
Logarithmic and exponential functions can be used to model real-world situations. Logarithmic functions are very helpful when working with phenomena that have a very wide range of values, because they allow you to keep the values you actually work with in a smaller range. Exponential functions are helpful with phenomena that change very quickly, or that grow or decay by a percentage over a particular time period.
