Introduction to Natural and Common Logarithms
Learning Objective(s)
· Use a calculator to find logarithms or powers of base e.
· Graph exponential and logarithmic functions of base e.
· Find logarithms to bases other than e or 10 by using the change of base formula.
Introduction
In both exponential functions and logarithms, any number can be the base. However, there are two bases that are used so frequently that mathematicians have special names for their logarithms, and scientific and graphing calculators include keys specifically for them! These are the common and natural logarithms.
Common Logarithms and e
A common logarithm is any logarithm with base 10. Recall that our number system is base 10; there are ten digits from 0-9, and place value is determined by groups of ten. You can remember a “common logarithm,” then, as any logarithm whose base is our “common” base, 10.
Natural logarithms are different than common logarithms. While the base of a common logarithm is 10, the base of a natural logarithm is the special number e. Although this looks like a variable, it represents a fixed irrational number approximately equal to 2.718281828459. (Like pi, it continues without a repeating pattern in its digits.) e is sometimes called Euler′s number or Napier’s constant, and the letter e was chosen to honor the mathematician Leonhard Euler (pronounced oiler).
e is a complicated but interesting number. Let’s take a closer look at it through the lens of a formula you have seen before: compound interest.
The formula for compound interest is 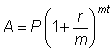 , where A is the amount of money after t years, P is the principal or initial investment, r is the annual interest rate (expressed as a decimal, not a percent), m is the number of compounding periods in a year, and t is the number of years.
, where A is the amount of money after t years, P is the principal or initial investment, r is the annual interest rate (expressed as a decimal, not a percent), m is the number of compounding periods in a year, and t is the number of years.
Imagine what happens when the compounding happens frequently. If interest is compounded annually, then m = 1. If compounded monthly, then m = 12. Compounding daily would be represented by m = 365; hourly would be represented by m = 8,760. You can see that as the frequency of the compounding periods increases, the value of m increases quickly. Imagine the value of m if interest were compounded each minute or each second!
You can even go more frequently than each second, and eventually get compounding continuously. Look at the values in this table, which looks a lot like the expression multiplied by P in the above formula. As x gets greater, the expression more closely resembles continuous compounding.
| x |
|
| 1 | 2 |
| 10 | 2.59374… |
| 100 | 2.70481… |
| 1000 | 2.71692… |
| 10,000 | 2.71814… |
| 100,000 | 2.71826… |
| 1,000,000 | 2.71828… |
Notice that although x is increasing a lot (multiplying by 10 each time!), the value of 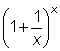 is not increasing wildly. In fact, it is getting closer and closer to 2.718281828459…or the value now called e.
is not increasing wildly. In fact, it is getting closer and closer to 2.718281828459…or the value now called e.
The function f(x) = ex has many applications in economics, business, and biology. e is an important number for this reason.
Scientific and graphing calculators all have keys that help you work with e. Look on your calculator and find one labeled “e” or “exp.” (Some graphing calculators may require you to use a menu to find e. If you can’t see the key, consult your manual or ask your instructor.)
How to evaluate exponential expressions using e (such as e3) depends on your calculator. On some calculators you press the [ex] key first then enter the exponent and press enter. On others you enter the exponent first then press the [ex] key. It is important that you know how your calculator works. With your calculator, try finding e3. The result should be 20.0855369… (the number of digits displayed will also depend on your calculator).
| Example | ||
| Problem | Find e1.5 using a calculator. Round your answer to the nearest hundredth. | |
|
|
| Enter the keystrokes needed for your calculator. If you are having trouble getting the correct answer, consult your manual or instructor. |
|
| 4.4816890… | Calculator result. Then round the answer to the nearest hundredth. |
| Answer | 4.48 | To see this worked out on a calculator, see the Worked Examples for this topic. |
You can find powers of 10 (the common base) in the same way. Some calculators have a [10^] or [10x] key that you can use to find powers of 10. Another way to find powers of 10 is to use the [xy] or the [yx] key that will work with any base (although if you use this method, you will have to key in two numbers—the base, 10, and whatever exponent you are raising it to).
| Example | ||
| Problem | Find 101.5, using a calculator. Round your answer to the nearest hundredth. | |
|
|
| Enter the keystrokes needed for your calculator. If you are having trouble getting the correct answer, consult your manual or instructor. |
|
| 31.6227766… | Calculator result. Then round the answer to the nearest hundredth. |
| Answer | 31.62 | To see this worked out on a calculator, see the Worked Examples for this topic. |
Natural logarithms (using e as the base) and common logarithms (using 10 as the base) are also available on scientific and graphing calculators. When a logarithm is written without a base, you should assume the base is 10. For example:
log 100 = log10100 = 2
Natural logarithms also have their own symbol: ln.
ln 100 = loge100 = 4.60517…
The logarithm keys are often easier to find, but they may work differently from one calculator to the next. Most handheld scientific calculators require you to provide the input first, then press the [log] (common) or [ln] (natural) key. Other calculators work in reverse: press the [log] or [ln] key, and then provide the input and press [Enter] or [=].
On your calculator, find the common logarithm ([log] or [log10]) key and the natural logarithm ([ln]) key and verify that ln 100 = loge100 = 4.60517….
| Example | ||
| Problem | Find ln 3, using a calculator. Round your answer to the nearest hundredth. | |
|
|
| Remember ln means “natural logarithm,” or loge. Enter the keystrokes needed for your calculator. If you are having trouble getting the correct answer, consult your manual or instructor. |
|
| 1.098612… | Calculator result. Then round the answer to the nearest hundredth. |
| Answer | 1.10 | To see this worked out on a calculator, see the Worked Examples for this topic. |
| Example | ||
| Problem | Find log 34, using a calculator. Round your answer to the nearest hundredth. | |
|
|
| Remember, when no base is specified, this is the common logarithm (base 10). Enter the keystrokes needed for your calculator. If you are having trouble getting the correct answer, consult your manual or instructor. |
|
| 1.5314789… | Calculator result. Then round the answer to the nearest hundredth. |
| Answer | 1.53 | To see this worked out on a calculator, see the Worked Examples for this topic. |
| Use a calculator to find ln 7.
A) 0.845098… B) 1.945910… C) 1096.633… D) 10,000,000
|
Graphing functions with the base e is no different than graphing other exponential and logarithmic functions: Create a table of values, plot the points, and connect them with a smooth curve. You will want to use a calculator when creating the table.
| Example | ||||||||||||||
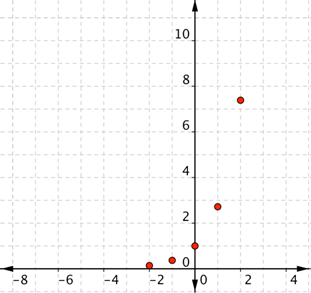
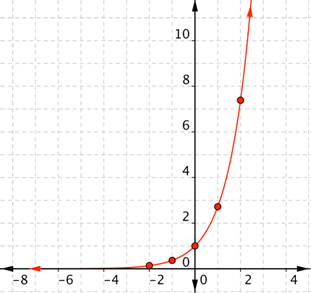
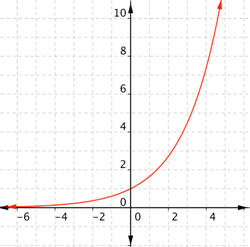
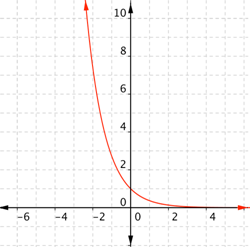
| Problem | Graph f(x) = ex. |
| ||||||||||||
|
|
| Start with a table of values. Don’t forget to choose positive and negative values for x.
Use a calculator to find the f(x) values. | ||||||||||||
|
|
| If you think of f(x) as y, each row forms an ordered pair that you can plot on a coordinate grid. | ||||||||||||
|
|
| Plot the points. | ||||||||||||
| Answer |
| Connect the points as best you can, using a smooth curve (not a series of straight lines). Use the shape of an exponential graph to help you: the graph gets close to the x-axis on the left, and gets steeper and steeper on the right. | ||||||||||||
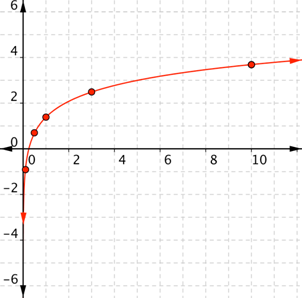
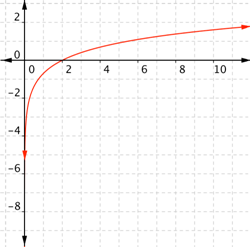
The same process works for logarithmic functions. Choose x values and use a calculator to find the y values.
| Example | |||||||||||||||||||||||
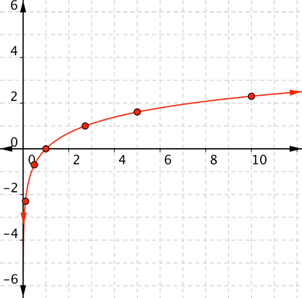
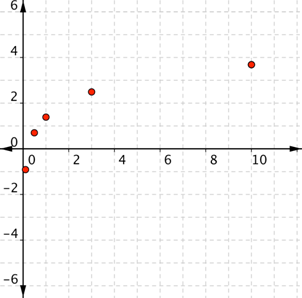
| Problem | Graph f(x) = ln x. |
| |||||||||||||||||||||
|
|
| Start with a table of values. If you choose x values, remember that x must be greater than 0. Choose values greater than and less than the base. The base and 1 are also good choices for x values.
| |||||||||||||||||||||
|
|
| If you think of f(x) as y, each row forms an ordered pair that you can plot on a coordinate grid. | |||||||||||||||||||||
|
|
| Plot the points.
| |||||||||||||||||||||
| Answer |
| Connect the points as best you can, using a smooth curve (not a series of straight lines). Use the shape of a logarithmic graph to help you: the graph gets close to the y-axis for x near 0. | |||||||||||||||||||||
Sometimes the inputs to the logarithm, or the exponent on the base, will be more complicated than just a single variable. In those cases, be sure to use the correct input on the calculator.
Note: If your calculator uses the “input last” method for logarithms, either calculate the input separately and write it down, or use parentheses to be sure the correct input is used. For example, when calculating log(3x) when x = 4, the correct answer is 1.079… . If you don’t use the parentheses, the calculator will find log 3, and multiply that by 4 to get 1.908… .
| Example | ||||||||||||||||||||
| Problem | Graph f(x) = ln 4x. |
| ||||||||||||||||||
|
|
| Create a table of values. Although everything could be done using the calculator, let’s include a column for the input of the logarithm. This helps you avoid calculator errors. | ||||||||||||||||||
|
|
| Use the table pairs to plot points. You may want to choose additional values for the table to give a better idea for the entire visible graph.
| ||||||||||||||||||
| Answer |
| Connect the points as best you can, using a smooth curve. | ||||||||||||||||||
| Which of the following is a graph for f(x) =e0.5x?
A) B)
C) D)
|
Now you know how to find base 10 and base e logarithms of any number. What if you wanted to calculate log736? Converting to an exponential equation, you have 7x = 36. You know 71 is 7, and 72 is 49, so you can reason that x must be between 1 and 2, probably very close to 2. But how close? You don’t have a key for base 7, so you use a Change of Base formula to change the base of a log function to another base.
| Change of Base formula
|
Notice that a appears as the base in both logarithms on the right side of the formula. For example,![]() , using a new base of 10. You could also say
, using a new base of 10. You could also say ![]() , or even
, or even ![]() . Of course, that last one isn’t any easier to calculate than the original expression—but using the [log] or [ln] keys on a calculator, you can use
. Of course, that last one isn’t any easier to calculate than the original expression—but using the [log] or [ln] keys on a calculator, you can use ![]() or
or ![]() to find log7 36.
to find log7 36.
| Example | ||
| Problem | Find log7 36. |
|
|
|
| Use the Change of Base formula. You can use common logarithms or natural logarithms. For this example, let’s use common logarithms. |
|
|
| Use the calculator to evaluate the quotient. |
| Answer | 1.84156… |
|
If you had used natural logarithms, you would have gotten the same answer:
![]()
| Example | ||
| Problem | Find log3 25.9. |
|
|
|
| Use the Change of Base formula. This time, let’s use natural logarithms. |
|
|
| Evaluate the quotient. |
| Answer | 2.9621 |
|
| Find log5 200.
A) 40 B) 0.303… C) 3.292… D) 2.301…
|
Summary
Common logarithms (base 10, written log x without a base) and natural logarithms (base e, written ln x) are used often. Scientific and graphing calculators have keys or menu items that allow you to easily find log x and ln x, as well as 10x and ex. Using these keys and the change of base formula, you can find logarithms in any base.