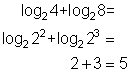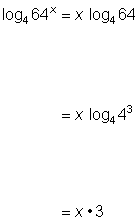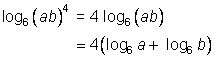Properties of Logarithmic Functions
Learning Objective(s)
· Express the logarithm of a product as a sum of logarithms.
· Express the logarithm of a quotient as a difference.
· Express the logarithm of a power as a product.
· Simplify logarithmic expressions.
Introduction
Throughout your study of algebra, you have come across many properties—such as the commutative, associative, and distributive properties. These properties help you take a complicated expression or equation and simplify it.
The same is true with logarithms. There are a number of properties that will help you simplify complex logarithmic expressions. Since logarithms are so closely related to exponential expressions, it is not surprising that the properties of logarithms are very similar to the properties of exponents. As a quick refresher, here are the exponent properties.
| Properties of Exponents
Product of powers: Quotient of powers: Power of a power:
|
One important but basic property of logarithms is logb bx = x. This makes sense when you convert the statement to the equivalent exponential equation. The result? bx = bx.
Let’s find the value of y in![]() . Remember
. Remember ![]() , so
, so ![]() means
means ![]() and y must be 2, which means
and y must be 2, which means ![]() . You will get the same answer that
. You will get the same answer that ![]() equals 2 by using the property that logb bx = x.
equals 2 by using the property that logb bx = x.
Remember that the properties of exponents and logarithms are very similar. With exponents, to multiply two numbers with the same base, you add the exponents. With logarithms, the logarithm of a product is the sum of the logarithms.
|
Logarithm of a Product
The logarithm of a product is the sum of the logarithms: logb (MN) = logb M + logb N
|
Let’s try the following example.
| Example | ||
| Problem | Use the product property to rewrite | |
|
|
| Use the product property to write as a sum. |
|
|
| Simplify each addend, if possible. In this case, you can simplify both addends. Rewrite log2 4 as log2 22and log2 8 as log2 23, then use the property logb bx = x. Or, rewrite log2 4 = y as 2y = 4 to find y = 2, and log2 8 = y as 2y = 8 to find y = 3. Use whatever method makes sense to you. |
| Answer |
|
|
Another way to simplify ![]() would be to multiply 4 and 8 as a first step.
would be to multiply 4 and 8 as a first step.
![]()
You get the same answer ![]() as in the example!
as in the example!
Notice the similarity to the exponent property: bmbn = bm + n, while logb (MN) = logb M + logb N. In both cases, a product becomes a sum.
| Example | ||
| Problem | Use the product property to rewrite log3 (9x). | |
|
| log3 (9x) = log3 9 + log3 x | Use the product property to write as a sum. |
|
| log3 9 + log3 x = log3 32 + log3 x = 2 + log3 x | Simplify each addend, if possible. In this case, you can simplify log3 9 but not log3 x. Rewrite log3 9 as log3 32, then use the property logb bx = x. Or, simplify log3 9 by converting log3 9 = y to 3y = 9 and finding that y = 2.
Use whatever method makes sense to you. |
| Answer | log3(9x) = 2 + log3 x |
|
If the product has many factors, you just add the individual logarithms:
logb (ABCD) = logb A + logb B + logb C + logb D.
| Rewrite log2 8a, then simplify.
A) 3 log2 a B) log2 3a C) log2 (3 + a) D) 3 + log2 a
|
You can use the similarity between the properties of exponents and logarithms to find the property for the logarithm of a quotient. With exponents, to multiply two numbers with the same base, you add the exponents. To divide two numbers with the same base, you subtract the exponents. What do you think the property for the logarithm of a quotient will look like?
As you may have suspected, the logarithm of a quotient is the difference of the logarithms.
| Logarithm of a Quotient
|
With both properties: ![]() and
and![]() , a quotient becomes a difference.
, a quotient becomes a difference.
| Example |
| ||
| Problem | Use the quotient property to rewrite |
| |
|
| log2 | Use the quotient property to rewrite as a difference. | |
| Answer |
| The first expression can’t be simplified further. However, the second expression can be simplified. What exponent on the base (2) gives a result of 2? Since 21 = 2, you know log2 2 = 1. | |
| Which of these is equivalent to:
A) 4 – log3 a B) C) log3 (4 – a) D)
|
The remaining exponent property was power of a power: ![]() . The similarity with the logarithm of a power is a little harder to see.
. The similarity with the logarithm of a power is a little harder to see.
| Logarithm of a Power
|
With both properties, ![]() and
and![]() , the power “n” becomes a factor.
, the power “n” becomes a factor.
| Example | ||
| Problem | Use the power property to simplify log3 94. | |
|
| log3 94 = 4 log3 9
| You could find 94, but that wouldn’t make it easier to simplify the logarithm. Use the power property to rewrite log3 94 as 4log3 9. |
|
| 4 log3 9 = 4•2 | You may be able to recognize by now that since 32 = 9, log3 9 = 2. |
| Answer | log3 94 = 8 | Multiply the factors. |
Notice in this case that you also could have simplified it by rewriting it as 3 to a power: log3 94 = log3 (32)4. Using exponent properties, this is log3 38 and by the property logb bx = x, this must be 8!
| Example | |||
| Problem | Use the properties of logarithms to rewrite log4 64x. | ||
|
|
| Use the power property to rewrite
Rewrite Or, you may be able to recognize by now that since 43 = 64, log464 = 3. | |
|
|
|
| |
| Answer | log4 64x = 3x | Multiply the factors. | |
| Which of these is equivalent to: log2 x8.
A) log2 3x B) 8 log2 x C) log2 8x D) 3 log2 x
|
The properties can be combined to simplify more complicated expressions involving logarithms.
| Example | ||
| Problem | Use the properties of logarithms to expand | |
|
|
|
|
|
|
| Use the quotient property to rewrite |
|
|
| Now you have two logarithms, each with a product. Apply the product rule to each.
Be careful with the subtraction! Since all of log10 cd is subtracted, you have to subtract both parts of the term, (log10 c + log10 d). |
| Answer |
|
|
| Example | ||
| Problem | Simplify log6 (ab)4, writing it as two separate terms. | |
|
|
|
|
|
|
| Use the power property to rewrite log6 (ab)4 as 4 log6 (ab).
You are taking the log of a product, so apply the product property.
Be careful: the value 4 is multiplied by the whole logarithm, so use parentheses when you rewrite log6 (ab) as (log6 a + log6 b) |
| Answer | log6 (ab)4 = 4 log6 a + 4 log6 b
| Use the distributive property. |
| Simplify log3 x2y.
A) 2(log3 x + log3 y) B) log3 x2 + log3 y C) 2 log3 xy D) 2 log3 x + log3 y
|
Summary
Like exponents, logarithms have properties that allow you to simplify logarithms when their inputs are a product, a quotient, or a value taken to a power. The properties of exponents and the properties of logarithms have similar forms.
|
| Exponents | Logarithms |
| Product Property |
|
|
| Quotient Property |
|
|
| Power Property |
|
|
Notice how the product property leads to addition, the quotient property leads to subtraction, and the power property leads to multiplication for both exponents and logarithms.