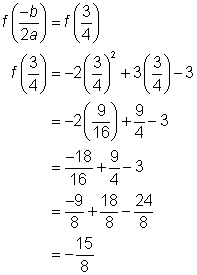Graphing Types of Functions
Learning Objective(s)
· Graph linear functions.
· Graph quadratic functions.
· Graph radical functions.
Introduction
When both the input (independent variable) and the output (dependent variable) are real numbers, a function can be represented by a coordinate graph. The input is plotted on the x-axis and the output is plotted on the y-axis.
A helpful first step in graphing a function is to make a table of values. This is particularly useful when you don’t know the general shape the function will have. You probably already know that a linear function will be a straight line, but let’s make a table first to see how it can be helpful.
When making a table, it’s a good idea to include negative values, positive values, and zero to ensure that you do have a linear function.
| Example | ||||||||||||||
| Problem | Make a table of values for f(x) = 3x + 2. | |||||||||||||
|
|
| Make a two-column table. Label the columns x and f(x). | ||||||||||||
|
|
| Choose several values for x and put them as separate rows in the x column.
Tip: It’s always good to include 0, positive values, and negative values, if you can. | ||||||||||||
|
|
| Evaluate the function for each value of x, and write the result in the f(x) column next to the x value you used. When x = 0, f(0) = 3(0) + 2 = 2, f(1) = 3(1) + 2 = 5 f(−1) = 3(−1) + 2 = −3 + 2 = −1, and so on.
| ||||||||||||
| Possible Answer |
| (Note that your table of values may be different from someone else’s, you may each choose different numbers for x.) | ||||||||||||
Now that you have a table of values, you can use them to help you draw both the shape and location of the function. Important: The graph of the function will show all possible values of x and the corresponding values of y. This is why the graph is a line and not just the dots that make up the points in our table.
| Example | ||||||||||||||
| Problem | Graph f(x) = 3x + 2. |
| ||||||||||||
|
|
| Start with a table of values, like the one in the previous example.
If you think of f(x) as y, each row forms an ordered pair that you can plot on a coordinate grid. | ||||||||||||
|
|
| Plot the points. | ||||||||||||
| Answer |
| Since the points lie on a line, use a straight edge to draw the line. Try to go through each point without moving the straight edge. | ||||||||||||
Let’s try another one.
| Example | ||||||||||||||
| Problem | Graph f(x) = −x + 1. |
| ||||||||||||
|
| f(−2) = − (−2) + 1 = 2 + 1 = 3 f(−1) = − (−1) + 1 = 1 + 1 = 2 f(0) = − (0) + 1 = 0 + 1 = 1 f(1) = − (1) + 1 = −1 + 1 = 0 f(2) = − (2) + 1 = −2 + 1 = −1
| Start with a table of values. You can choose different values for x, but once again, it’s helpful to include 0, some positive values, and some negative values.
If you think of f(x) as y, each row forms an ordered pair that you can plot on a coordinate grid. | ||||||||||||
|
|
| Plot the points. | ||||||||||||
| Answer |
| Since the points lie on a line, use a straight edge to draw the line. Try to go through each point without moving the straight edge. | ||||||||||||
These graphs are representations of a linear function. Remember that a function is a correspondence between two variables, such as x and y.
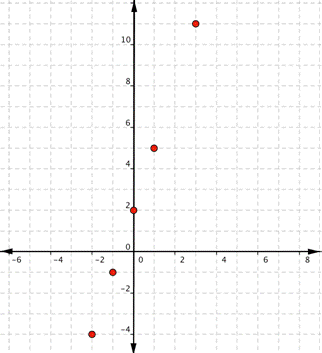
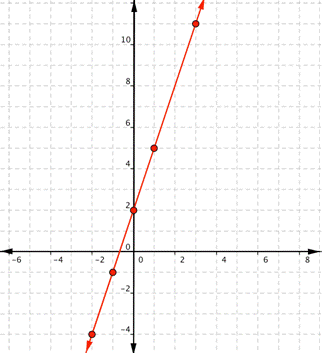
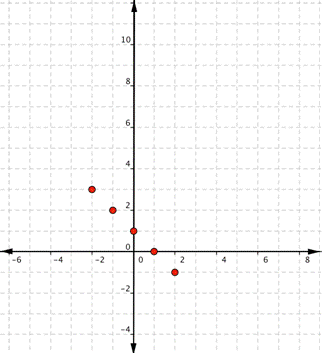
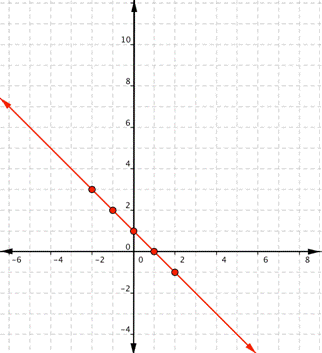
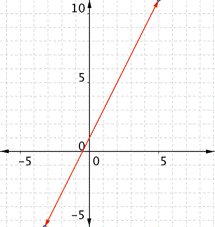
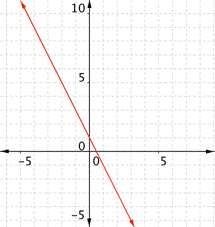
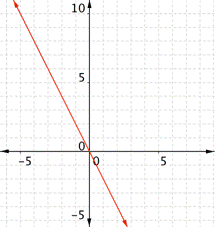
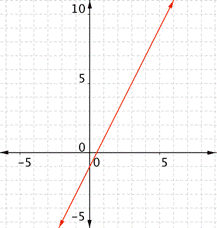
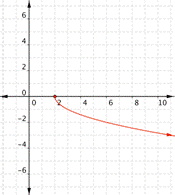
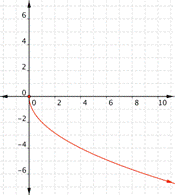
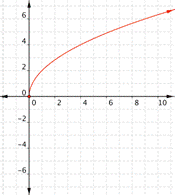
| Graph f(x) = 2x – 1. Which of the following graphs is correct?
A) B)
C) D)
|
, 0). The correct answer is Graph D.
Nonlinear functions can also be graphed. It’s helpful to have an idea what the shape should be, so you can be sure that you’ve chosen enough points to plot as a guide. Let’s start with the most basic quadratic function, f(x) = x2.
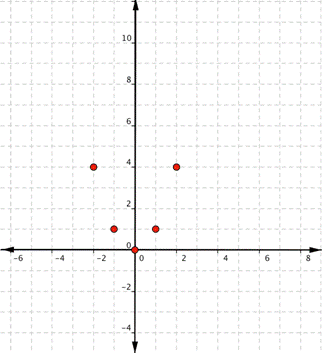
| Example | ||||||||||||||
| Problem | Graph f(x) = x2. |
| ||||||||||||
|
|
| Start with a table of values. Then think of the table as ordered pairs. | ||||||||||||
|
|
| Plot the points. | ||||||||||||
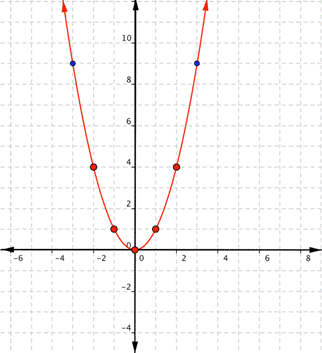
| Answer |
| Since the points are not on a line, you can’t use a straight edge. Connect the points as best you can, using a smooth curve (not a series of straight lines). You may want to find and plot additional points (such as the ones in blue here). | ||||||||||||
Notice that the shape is like the letter U. This is called a parabola. One-half of the parabola is a mirror image of the other half. The line that goes down the middle is called the line of reflection, in this case that line is they y-axis.
The equations for quadratic functions have the form f(x) = ax2 + bx + c where 
. In the basic graph above, a = 1, b = 0, and c = 0. Here are some graphs with different values for a, b, and c. Notice how each value changes the shape and location of the parabola.
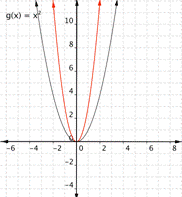
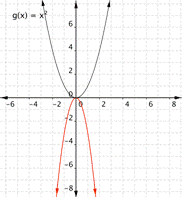
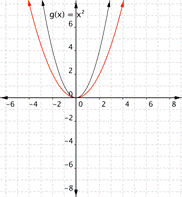
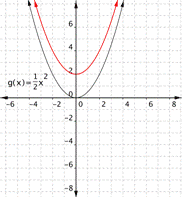
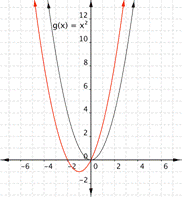
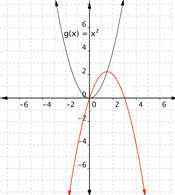
Changing a changes the width of the parabola and whether it opens up (a > 0) or down (a < 0).
|
|
|
|
|
|
|
|
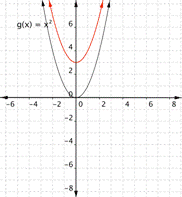
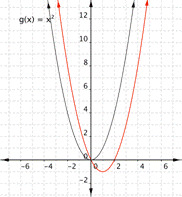
If there is no b term, changing c moves the parabola up or down so that the y intercept is (0, c).
|
|
|
|
|
|
|
|
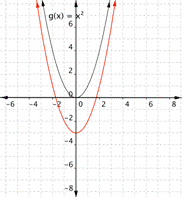
Changing b moves the line of reflection. The way it moves depends also on a.
|
|
|
|
|
|
|
|
| Properties of a Parabola
For
|
, where a, b, and c are real numbers.
, 
).
| Example | ||||||||||||||
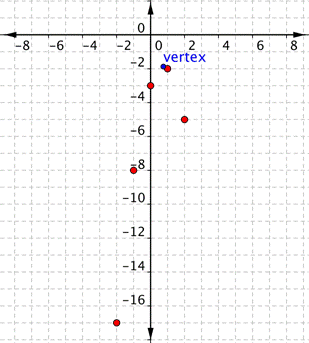
| Problem | Graph f(x) = −2x2 + 3x – 3. |
| ||||||||||||
|
| a = −2, so the graph will open down and be thinner than f(x) = x2.
c = −3, so it will move to intercept the y-axis at | Before making a table of values, look at the values of a and c to get a general idea of what the graph should look like. | ||||||||||||
|
|
| Create a table of values. Notice that in this table, the x values increase. The y values increase and then start to decrease again. That indicates a parabola. | ||||||||||||
|
| Vertex formula = x-coordinate of vertex:
y-coordinate of vertex:
Vertex: | To find the vertex of the parabola, use the formula | ||||||||||||
|
|
| Use the table pairs to plot points. Note the vertex, | ||||||||||||
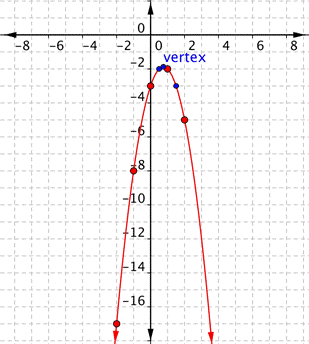
| Answer |
| Connect the points as best you can, using a smooth curve. Remember that the parabola is two mirror images, so if your points don’t have pairs with the same value, you may want to include additional points (such as the ones in blue here). Plot points on either side of the vertex. x = | ||||||||||||
are good values to include.
| Would the graph for f(x) = −3x2 + 2x – 1 open up or down, and why?
A) Up, because a (the coefficient of x2) is negative. B) Down, because a (the coefficient of x2) is negative. C) Up, because b (the coefficient of x) is positive. D) Down, because b (the coefficient of x) is positive.
|
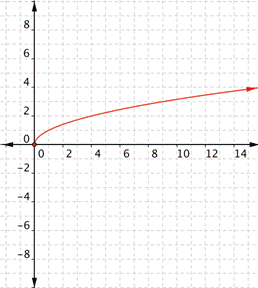
You can also graph radical functions (such as square root functions) by choosing values for x and finding points that will be on the graph. Again, it’s helpful to have some idea about what the graph will look like.
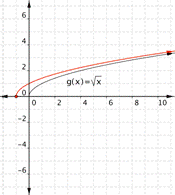
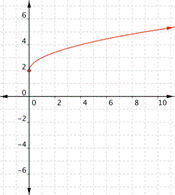
Think about the basic square root function, 
. Let’s take a look at a table of values for x and y and then graph the function. (Notice that all the values for x in the table are perfect squares. Since you are taking the square root of x, using perfect squares makes more sense than just finding the square roots of 0, 1, 2, 3, 4, etc.)
| x | f(x) |
| 0 | 0 |
| 1 | 1 |
| 4 | 2 |
| 9 | 3 |
| 16 | 4 |
Recall that x can never be negative here because the square root of a negative number would be imaginary, and imaginary numbers cannot be graphed. There are also no values for x that will result in y being a negative number. Take a look at the graph.
As with parabolas, multiplying and adding numbers makes some changes, but the basic shape is still the same. Here are some examples.
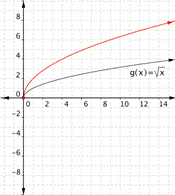
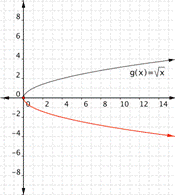
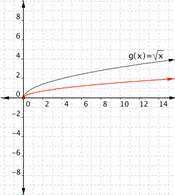
Multiplying 
by a positive value changes the width of the half-parabola. Multiplying by a negative number gives you the other half of a horizontal parabola.
|
|
|
|
|
|
|
|
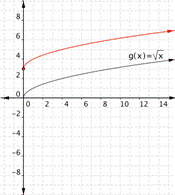
Adding a value outside the radical moves the graph up or down. Think about it as adding the value to the basic y value of , so a positive value added moves the graph up.
|
|
|
|
|
|
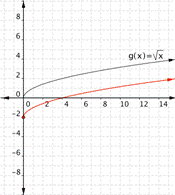
Adding a value inside the radical moves the graph left or right. Think about it as adding a value to x before you take the square root—so the y value gets moved to a different x value. For example, for , the square root is 3 if x = 9. For
, the square root is 3 when x + 1 is 9, so x is 8. Changing x to x +1 shifts the graph to the left by 1 unit (from 9 to 8). Changing x to x − 2 shifts the graph to the right by 2 units.
|
|
|
|
|
|
Notice that as x gets greater, adding or subtracting a number inside the square root has less of an effect on the value of y!
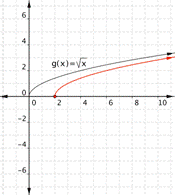
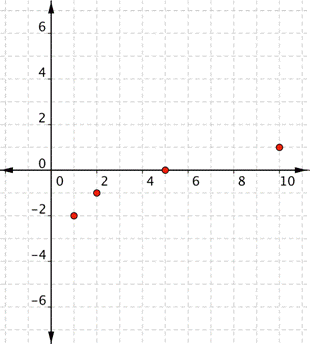
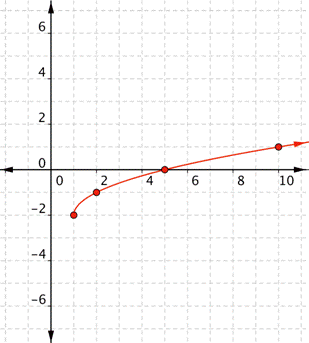
| Example | ||||||||||||
| Problem | Graph |
| ||||||||||
|
| Inside the square root, you’re subtracting 1, so the graph will move to the right 1 from the basic
You’re also adding −2 outside the square root, so the graph will move down two from the basic | Before making a table of values, look at the function equation to get a general idea what the graph should look like. | ||||||||||
|
|
| Create a table of values. Choose values that will make your calculations easy. You want x – 1 to be a perfect square (0, 1, 4, 9, and so on) so you can take the square root.
Since values of x less than 1 makes the value inside the square root negative, there will be no points on the coordinate graph to the left of x = 1. There is no need to choose x values less than 1 for your table! | ||||||||||
|
|
| Use the table pairs to plot points. | ||||||||||
| Answer |
| Connect the points as best you can, using a smooth curve. | ||||||||||
.
| Which of the following is a graph of
A) B)
C) D)
|
?
is entirely under the x-axis, in Quadrant IV. The graph of 
. The graph of
Summary
Creating a graph of a function is one way to understand the relationship between the inputs and outputs of that function. Creating a graph can be done by choosing values for x, finding the corresponding y values, and plotting them. However, it helps to understand the basic shape of the function. Knowing the effect of changes to the basic function equation is also helpful.
One common shape you will see is a parabola. Parabolas have the equation
f(x) =ax2 +bx + c , where a, b, and c are real numbers and . The value of a determines the width and the direction of the parabola, while the vertex depends on the values of a, b and c. The vertex is 
.
