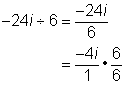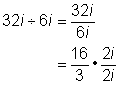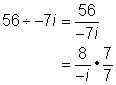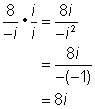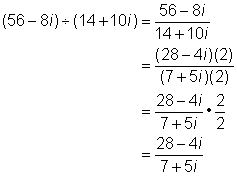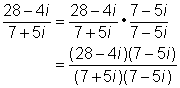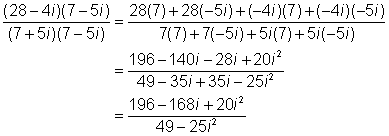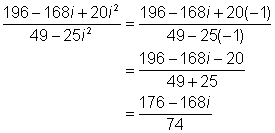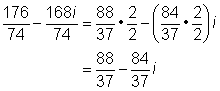Operations with Complex Numbers

 

Learning Objective(s)

·         Add complex numbers.

·         Subtract complex numbers.

·         Multiply complex numbers.

·         Find conjugates of complex numbers.

·         Divide complex numbers.

 

Any time new kinds of numbers are introduced, one of the first questions that needs to be addressed is, “How do you add them?” In this topic, you’ll learn how to add complex numbers and also how to subtract, multiply, and divide them.

 

First, consider the following expression.

 

(6x + 8) + (4x + 2)

 

To simplify this expression, you combine the like terms, 6x and 4x. These are like terms because they have the same variable with the same exponents. Similarly, 8 and 2 are like terms because they are both constants, with no variables.

 

(6x + 8) + (4x + 2) = 10x + 10

 

In the same way, you can simplify expressions with radicals.

 

 

You can add  to  because the two terms have the same radical, , just as 6x and 4x have the same variable and exponent.

 

The number i looks like a variable, but remember that it is equal to . The great thing is you have no new rules to worry about—whether you treat it as a variable or a radical, the exact same rules apply to adding and subtracting complex numbers. You combine the imaginary parts (the terms with i), and you combine the real parts.

 

 

 

 

 

 

Subtract. (5 + 3i) – (3 – i)   A) 2 + 4i   B) 6   C) 2 + 2i   D) 8 + 2i   Show/Hide Answer A) 2 + 4i Correct. Distributing the subtraction to the second complex number gives 5 + 3i – 3 + i. Rearranging to put like terms together gives 5 – 3 + 3i + i, and combining like terms gives 2 + 4i.   B) 6 Incorrect. You may have combined 5 + 3 from the first number (ignoring the i) and 3 – 1 from the second number (ignoring the i), giving that result of 8 - 2 = 6. Instead, you should distribute the subtraction across the second complex number to get 5 + 3i – 3 + i. Rearranging to put like terms together gives 5 – 3 + 3i + i, and combining like terms gives the correct answer 2 + 4i.   C) 2 + 2i Incorrect. You probably forgot to distribute the subtraction to the imaginary part of the second complex number, leaving it as – i instead of + i. Distributing the subtraction to the second complex number gives 5 + 3i – 3 + i. Rearranging to put like terms together gives 5 – 3 + 3i + i, and combining like terms gives the correct answer 2 + 4i.   D) 8 + 2i Incorrect. You may have added instead of subtracting. Distributing the subtraction to the second complex number gives 5 + 3i – 3 + i. Rearranging to put like terms together gives 5 – 3 + 3i + i, and combining like terms gives the correct answer 2 + 4i.

 

 

Again, consider the following expression. Before reading further, consider how you would simplify it.

 

(5x)(−3x)

 

You can simplify by multiplying the coefficients together, then the variables.

 

 

Multiplying two imaginary (but not complex!) numbers together works in a similar way, but there is an additional step. Start with the same method to multiply 5i and −3i.

 

 

 

This seems fine so far, but the i² can be simplified further.

 

When you multiply a square root by itself, you get the number under the radical. This is what square root means.

 

 

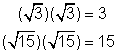
Well, i is also a square root. It’s equal to .

 

 

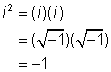
So, the final step to simplifying (5i)( −3i) = −15i² is to replace i² with −1.

 

 

 

 

 

Notice that the product of two imaginary numbers is a real number! We will see this again when we multiply two complex numbers.

 

 

Multiply and simplify. (3i)( −i)   A) 3   B) −3   C) 3i   D) −3i2   Show/Hide Answer A) 3 Correct. (3i)( −i) = 3(-1)(i)(i) = −3i2 = −3(−1) = 3.   B) −3 Incorrect. You probably either missed the sign on the second factor, or you incorrectly replaced i2. (3i)( −i) = 3(−1)(i)(i) = −3i2 = −3(−1) = 3.   C) 3i Incorrect. You probably incorrectly multiplied (i)( −i), or incorrectly replaced i2. (3i)( −i) = 3(−1)(i)(i) = −3i2 = −3(−1) = 3.   D) −3i2 Incorrect. This is a correct multiplication, but i2 can be simplified further. (3i)( −i) = 3(−1)(i)(i) = −3i2 = −3(−1) = 3.

 

 

The following expression is a little more complicated because two binomials are being multiplied. This means you have to use the Distributive Property of Multiplication. (Remember that multiplying using the FOIL method—First, Outside, Inside, Last—is an application of the distributive property of multiplication.) Once the binomials have been multiplied, simplify the expression by combining like terms.

 

 

 

Again, in the same way, you can multiply complex numbers. At the end, you will need to simplify i².

 

 

 

 

In this case, the product of two complex numbers is complex. But in the following example, the product is real, not complex. See if you can figure out why!

 

 

 

 

Just as  and  are conjugates, 6 + 8i and 6 – 8i are conjugates. (Again, i is a square root, so this isn’t really a new idea.) When the numbers are complex, they are called complex conjugates. Because conjugates have terms that are the same except for the operation between them (one is addition and one is subtraction), the i terms in the product will add to 0. In the example above, −48i was added to 48i, and that sum is 0, so there was no i term in the final product. That means the product of complex conjugates will always be a real (not complex) number.

 

 

Multiply. (9 + i)(9 – i)   A) 82 + 18i   B) 80 – 18i   C) 80   D) 82   Show/Hide Answer A) 82 + 18i Incorrect. Don’t forget to use the FOIL method so that every term in the first complex number is multiplied by every term in the other complex number. Since the factors are complex conjugates, their product should be a real number. (9 + i)(9 – i) = 81 – 9i + 9i – i2 = 81 – i2 = 81 – (−1) = 81 + 1 = 82.   B) 80 – 18i Incorrect. Don’t forget to use the FOIL method so that every term in the first complex number is multiplied by every term in the other complex number. Since the factors are complex conjugates, their product should be a real number. (9 + i)(9 – i) = 81 – 9i + 9i – i2 = 81 – i2 = 81 – (−1) = 81 + 1 = 82.   C) 80 Incorrect. You probably multiplied correctly but forgot to subtract i2, or you forgot the negative when you multiplied i and -i. (9 + i)(9 – i )= 81 – 9i + 9i – i2 = 81 – i2 = 81 – (−1) = 81 + 1 = 82.   D) 82 Correct. (9 + i)(9 – i) = 81 – 9i + 9i – i2 = 81 – i2 = 81 – (−1) = 81 + 1 = 82.

 

 

So far, each operation with complex numbers has worked just like the same operation with radical expressions. This should no longer be a surprise—the number i is a radical, after all, so complex numbers are radical expressions!

 

Let’s look at division in two parts, like we did multiplication. First, let’s look at a situation in which the divisor is a monomial.

 

 

 

 

 

 

 

 

Simplify. 12 ÷ 10i   A)   B)   C)   D)   Show/Hide Answer A) Incorrect. When you simplify the numerical parts of , you still have i in the denominator. Rationalize the denominator of  by multiplying by : .   B) Correct. After simplifying the numerical parts of , you still have to rationalize the denominator because i is left in the denominator: .   C) Incorrect. When you rationalize the denominator, you have i2 in the denominator. Since i2 = −1, the quotient is negative. .   D) Incorrect. You may have forgotten the radical i in the denominator, or you may have made a mistake when you rationalized the denominator. When you rationalize the denominator, you must also multiply the numerator by i. .

 

 

When the divisor (that is, the denominator in the fraction) is a complex number with non-zero real and imaginary parts, you must rationalize the denominator using the complex conjugate. Remember that the product of a complex number with its complex conjugate is always a real number, so the denominator will be a real number. That means the result will be equivalent, but rationalized.

 

 

 

 

Simplify. (10 + 6i) ÷ (5 – 3i)   A)   B) 2 – 2i   C)   D)   Show/Hide Answer A) Correct. Write as a rational expression and multiply both numerator and denominator by the complex conjugate of the divisor: . This simplifies to .   B) 2 – 2i Incorrect. You probably just divided the real parts, then divided the coefficients of the imaginary parts. This works with addition and subtraction, but not division. Try writing the division as a rational expression, and multiply both numerator and denominator by the complex conjugate of the divisor. The correct answer is .   C) Incorrect. You probably correctly set up the rational expression and rationalized: . Remember at this point that i2 = −1, so subtracting 9i2 is the same as adding 9. The correct answer is . D) Incorrect. You probably correctly set up the rational expression and rationalized: . Remember at this point that the denominator (34) divides both terms in the numerator, so this simplifies to .

 

 

Operations with Complex Numbers   To add or subtract, combine like terms.   To multiply monomials, multiply the coefficients and then multiply the imaginary numbers i. If i2 appears, replace it with −1.   To multiply complex numbers that are binomials, use the Distributive Property of Multiplication, or the FOIL method. Multiply the resulting terms as monomials.   To divide, treat the quotient as a fraction. ·         Simplify the numerical parts, and then rationalize the denominator, if needed. ·         Replace i2 in both the numerator and the denominator with −1, as needed. ·        Write the answer in a + bi form, which may require further simplification of a and b when they are fractions.

 

 

Complex numbers can be added, subtracted, multiplied, and divided using the same ideas you used for radicals and variables. With multiplication and division, you may need to replace i² with −1 and simplify further.