Multiplying and Dividing Radical Expressions
Learning Objective(s)
· Multiply and simplify radical expressions that contain a single term.
· Divide and simplify radical expressions that contain a single term.
Introduction
You can do more than just simplify radical expressions. You can multiply and divide them, too. You can use your knowledge of exponents to help you when you have to operate on radical expressions this way.
Let’s start with a quantity that you have seen before,![]() . You can simplify this square root by thinking of it as
. You can simplify this square root by thinking of it as ![]() .
.
|
|
If you think of the radicand as a product of two factors (here, thinking about 64 as the product of 16 and 4), you can take the square root of each factor and then multiply the roots. The end result is the same, ![]() .
.
This is an example of the Product Raised to a Power Rule. This rule states that the product of two or more numbers raised to a power is equal to the product of each number raised to the same power.
This should be a familiar idea. You have applied this rule when expanding expressions such as (ab)x to ax • bx; now you are going to amend it to include radicals as well. Imagine that the exponent x is not an integer but is a unit fraction, like ![]() , so that you have the expression
, so that you have the expression ![]() . According to the Product Raised to a Power Rule, this can also be written
. According to the Product Raised to a Power Rule, this can also be written ![]() , which is the same as
, which is the same as ![]() , since fractional exponents can be rewritten as roots. So, for the same reason that
, since fractional exponents can be rewritten as roots. So, for the same reason that ![]() , you find that
, you find that ![]() .
.
A Product Raised to a Power Rule
For any numbers a and b and any integer x:
For any numbers a and b and any positive integer x:
For any numbers a and b and any positive integer x:
|
The Product Raised to a Power Rule is important because you can use it to multiply radical expressions. Note that the roots are the same—you can combine square roots with square roots, or cube roots with cube roots, for example. But you can’t multiply a square root and a cube root using this rule.
Let’s look at another example.
| Example | ||
| Problem | Simplify. | |
|
|
| Use the rule |
|
|
|
|
|
|
| Look for perfect squares in the radicand, and rewrite the radicand as the product of two factors. |
|
|
| Identify perfect squares. |
|
|
| Rewrite as the product of two radicals. |
|
|
| Simplify, using |
| Answer |
|
|
Using the Product Raised to a Power Rule, you can take a seemingly complicated expression, ![]() , and turn it into something more manageable,
, and turn it into something more manageable,![]() .
.
You may have also noticed that both ![]() and
and ![]() can be written as products involving perfect square factors. How would the expression change if you simplified each radical first, before multiplying?
can be written as products involving perfect square factors. How would the expression change if you simplified each radical first, before multiplying?
| Example | ||
| Problem | Simplify. |
|
|
|
| Look for perfect squares in each radicand, and rewrite as the product of two factors. |
|
|
| Identify perfect squares. |
|
|
| Rewrite as the product of radicals. |
|
|
| Simplify, using |
|
|
| Multiply. |
| Answer |
|
|
In both cases, you arrive at the same product, ![]() . It does not matter whether you multiply the radicands or simplify each radical first.
. It does not matter whether you multiply the radicands or simplify each radical first.
You multiply radical expressions that contain variables in the same manner. As long as the roots of the radical expressions are the same, you can use the Product Raised to a Power Rule to multiply and simplify. Look at the two examples that follow. In both problems, the Product Raised to a Power Rule is used right away and then the expression is simplified.
| Example | ||
| Problem | Simplify. | |
|
|
| Use the rule |
|
|
|
|
|
|
| Recall that |
|
|
|
|
|
|
| Look for perfect squares in the radicand. |
|
|
| Rewrite as the product of radicals. |
|
|
|
|
| Answer |
|
|
| Example | ||
| Problem | Simplify. |
|
|
|
| Notice that both radicals are cube roots, so you can use the rule |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Look for perfect cubes in the radicand. Since |
|
|
| Rewrite as the product of radicals. |
|
|
|
|
| Answer |
|
|
This next example is slightly more complicated because there are more than two radicals being multiplied. In this case, notice how the radicals are simplified before multiplication takes place. (Remember that the order you choose to use is up to you—you will find that sometimes it is easier to multiply before simplifying, and other times it is easier to simplify before multiplying. With some practice, you may be able to tell which is which before you approach the problem, but either order will work for all problems.)
| Example | ||
| Problem | Simplify. | |
|
|
| Notice this expression is multiplying three radicals with the same (fourth) root. Simplify each radical, if possible, before multiplying. Be looking for powers of 4 in each radicand. |
|
|
| Rewrite as the product of radicals. |
|
|
| Identify and pull out powers of 4, using the fact that |
|
|
| Since all the radicals are fourth roots, you can use the rule |
|
|
|
|
|
|
| Now that the radicands have been multiplied, look again for powers of 4, and pull them out. We can drop the absolute value signs in our final answer because at the start of the problem we were told |
| Answer |
|
|
| Which one of the following problem and answer pairs is incorrect?
A) Problem: B) Problem: C) Problem: D) Problem:
|
You can use the same ideas to help you figure out how to simplify and divide radical expressions. Recall that the Product Raised to a Power Rule states that ![]() . Well, what if you are dealing with a quotient instead of a product?
. Well, what if you are dealing with a quotient instead of a product?
There is a rule for that, too. The Quotient Raised to a Power Rule states that ![]() . Again, if you imagine that the exponent is a rational number, then you can make this rule applicable for roots as well:
. Again, if you imagine that the exponent is a rational number, then you can make this rule applicable for roots as well: 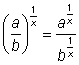 , so
, so ![]() .
.
A Quotient Raised to a Power Rule
For any real numbers a and b (b ≠ 0) and any positive integer x:
For any real numbers a and b (b ≠ 0) and any positive integer x:
|
As you did with multiplication, you will start with some examples featuring integers before moving on to more complex expressions like 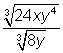 .
.
| Example | ||
| Problem | Simplify. |
|
|
|
| Use the rule |
|
|
| Simplify each radical. Look for perfect square factors in the radicand, and rewrite the radicand as a product of factors. |
|
|
| Identify and pull out perfect squares. |
|
|
|
|
|
|
| Simplify. |
| Answer |
|
|
| Example | ||
| Problem | Simplify. |
|
|
|
| Rewrite using the Quotient Raised to a Power Rule. |
|
|
| Simplify each radical. Look for perfect cubes in the radicand, and rewrite the radicand as a product of factors. |
|
|
| Identify and pull out perfect cubes. |
|
|
|
|
|
|
|
|
|
|
| You can simplify this expression even further by looking for common factors in the numerator and denominator. |
|
|
| Rewrite the numerator as a product of factors. |
|
|
| Identify factors of 1, and simplify. |
| Answer |
|
|
That was a lot of effort, but you were able to simplify using the Quotient Raised to a Power Rule. What if you found the quotient of this expression by dividing within the radical first, and then took the cube root of the quotient?
Let’s take another look at that problem.
| Example | ||
| Problem | Simplify. |
|
|
|
| Since both radicals are cube roots, you can use the rule |
|
|
| Within the radical, divide 640 by 40. |
|
|
| Look for perfect cubes in the radicand, and rewrite the radicand as a product of factors. |
|
|
| Identify perfect cubes and pull them out. |
|
|
|
|
|
|
| Simplify. |
| Answer |
|
|
That was a more straightforward approach, wasn’t it?
As with multiplication, the main idea here is that sometimes it makes sense to divide and then simplify, and other times it makes sense to simplify and then divide. Whichever order you choose, though, you should arrive at the same final expression.
Now let’s turn to some radical expressions containing variables. Notice that the process for dividing these is the same as it is for dividing integers.
| Example | ||
| Problem | Simplify. |
|
|
|
| Use the Quotient Raised to a Power Rule to rewrite this expression. |
|
|
| Simplify |
| Answer |
|
|
| Example | ||
| Problem | Simplify. |
|
|
|
| Use the Quotient Raised to a Power Rule to rewrite this expression. |
|
|
| Simplify |
|
|
| Identify perfect cubes and pull them out of the radical. |
|
|
|
|
|
|
| Simplify. |
| Answer |
|
|
As you become more familiar with dividing and simplifying radical expressions, make sure you continue to pay attention to the roots of the radicals that you are dividing. For example, while you can think of  as equivalent to
as equivalent to 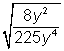 since both the numerator and the denominator are square roots, notice that you cannot express
since both the numerator and the denominator are square roots, notice that you cannot express  as
as 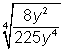 . In this second case, the numerator is a square root and the denominator is a fourth root.
. In this second case, the numerator is a square root and the denominator is a fourth root.
| Divide and simplify.
A)
B)
C)
D)
|
Summary
The Product Raised to a Power Rule and the Quotient Raised to a Power Rule can be used to simplify radical expressions as long as the roots of the radicals are the same. The Product Rule states that the product of two or more numbers raised to a power is equal to the product of each number raised to the same power. The same is true of roots: ![]() . When dividing radical expressions, the rules governing quotients are similar:
. When dividing radical expressions, the rules governing quotients are similar: ![]() .
.
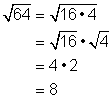
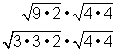
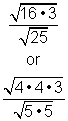
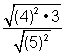
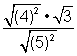
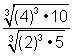
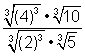
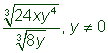
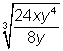
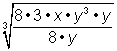
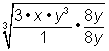
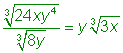
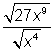 ,
, 