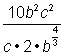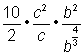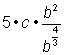Rational Exponents
Learning Objective(s)
· Convert radicals to expressions with rational exponents.
· Convert expressions with rational exponents to their radical equivalent.
· Use the laws of exponents to simplify expressions with rational exponents.
· Use rational exponents to simplify radical expressions.
Introduction
Square roots are most often written using a radical sign, like this, ![]() . But there is another way to represent the taking of a root. You can use rational exponents instead of a radical. A rational exponent is an exponent that is a fraction. For example,
. But there is another way to represent the taking of a root. You can use rational exponents instead of a radical. A rational exponent is an exponent that is a fraction. For example, ![]() can be written as
can be written as ![]() .
.
Can’t imagine raising a number to a rational exponent? They may be hard to get used to, but rational exponents can actually help simplify some problems. Let’s explore the relationship between rational (fractional) exponents and radicals.
Radicals and fractional exponents are alternate ways of expressing the same thing. You have already seen how square roots can be expressed as an exponent to the power of one-half.
| Radical Form | Exponent Form | Integer |
|
|
| 4 |
|
|
| 5 |
|
|
| 10 |
Let’s look at some more examples, but this time with cube roots. Remember, cubing a number raises it to the power of three. Notice that in these examples, the denominator of the rational exponent is the number 3.
| Radical Form | Exponent Form | Integer |
|
|
| 2 |
|
|
| 5 |
|
|
| 10 |
These examples help us model a relationship between radicals and rational exponents: namely, that the nth root of a number can be written as either ![]() or
or ![]() .
.
| Radical Form | Exponent Form |
|
|
|
|
|
|
|
|
|
| … | … |
|
|
|
When faced with an expression containing a rational exponent, you can rewrite it using a radical. In the table above, notice how the denominator of the rational exponent determines the index of the root. So, an exponent of ![]() translates to the square root, an exponent of
translates to the square root, an exponent of ![]() translates to the fifth root or
translates to the fifth root or ![]() , and
, and ![]() translates to the eighth root or
translates to the eighth root or ![]() .
.
| Example | ||
| Problem | Write | |
|
|
| The radical form |
| Answer |
|
|
| Example | ||
| Problem | Express | |
|
|
| Rewrite the expression with the fractional exponent as a radical. The denominator of the fraction determines the root, in this case the cube root.
The parentheses in |
| Answer |
|
|
Remember that exponents only refer to the quantity immediately to their left unless a grouping symbol is used. The example below looks very similar to the previous example with one important difference—there are no parentheses! Look what happens.
| Example | ||
| Problem | Express | |
|
|
| Rewrite the expression with the fractional exponent as a radical. The denominator of the fraction determines the root, in this case the cube root.
The exponent refers only to the part of the expression immediately to the left of the exponent, in this case x, but not the 2. |
| Answer |
|
|
Just as you can rewrite an expression with a rational exponent as a radical expression, you can express a radical expression using a rational exponent.
| Example | ||
| Problem | Express | |
|
|
| Rewrite the radical using a rational exponent. The root determines the fraction. In this case, the index of the radical is 3, so the rational exponent will be
Since 4 is outside the radical, it is not included in the grouping symbol and the exponent does not refer to it. |
| Answer |
|
|
| Example | ||
| Problem | Simplify. | |
|
|
| Rewrite the expression with the fractional exponent as a radical. |
|
|
6 • x2 | Find the square root of both the coefficient and the variable. |
| Answer |
|
|
Rational Exponents with Numerators Other than One
All of the numerators for the fractional exponents in the examples above were 1. You can use fractional exponents that have numerators other than 1 to express roots, as shown below. Notice any patterns within this table?
| Radical | Exponent |
|
|
|
|
|
|
|
|
|
|
|
|
| … | … |
|
|
|
To rewrite a radical using a fractional exponent, the power to which the radicand is raised becomes the numerator and the root becomes the denominator.
| Writing Fractional Exponents
Any radical in the form
|
The relationship between ![]() and
and ![]() works for rational exponents that have a numerator of 1 as well. For example, the radical
works for rational exponents that have a numerator of 1 as well. For example, the radical ![]() can also be written as
can also be written as ![]() , since any number remains the same value if it is raised to the first power. You can now see where the numerator of 1 comes from in the equivalent form of
, since any number remains the same value if it is raised to the first power. You can now see where the numerator of 1 comes from in the equivalent form of ![]() .
.
Let’s explore some radical expressions now and see how to simplify them. Here’s a radical expression that needs simplifying, ![]() .
.
One method of simplifying this expression is to factor and pull out groups of a3, as shown below in this example.
| Example | ||
| Problem | Simplify. |
|
|
|
| Rewrite by factoring out cubes. |
|
|
| Write each factor under its own radical and simplify. |
| Answer |
|
|
You can also simplify this expression by thinking about the radical as an expression with a rational exponent, and using the principle that any radical in the form ![]() can be written using a fractional exponent in the form
can be written using a fractional exponent in the form ![]() .
.
| Example | ||
| Problem | Simplify. |
|
|
|
| Rewrite the radical using a rational exponent. |
|
|
| Simplify the exponent. |
| Answer |
|
|
Note that rational exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
Both simplification methods gave the same result, a2. Depending on the context of the problem, it may be easier to use one method or the other, but for now, you’ll note that you were able to simplify this expression more quickly using rational exponents than when using the “pull-out” method.
Let’s try another example.
| Example | ||
| Problem | Simplify. |
|
|
|
| Rewrite the radical using rational exponents.
Use the rules of exponents to simplify the expression. |
|
|
|
|
|
|
| Change the expression with the rational exponent back to radical form. |
| Answer |
|
|
Again, the alternative method is to work on simplifying under the radical by using factoring. For the example you just solved, it looks like this.
| Example | ||
| Problem | Simplify. |
|
|
|
| Rewrite the expression. |
|
|
| Factor each radicand. |
|
|
| Simplify. |
| Answer |
|
|
| Which of the expressions below is equal to the expression
A)
B)
C)
D)
|
Let’s try a more complicated expression, ![]() . This expression has two variables, a fraction, and a radical. Let’s take it step-by-step and see if using fractional exponents can help us simplify it.
. This expression has two variables, a fraction, and a radical. Let’s take it step-by-step and see if using fractional exponents can help us simplify it.
Let’s start by simplifying the denominator, since this is where the radical sign is located.
| Example | |||
| Problem | Simplify. |
|
|
|
|
| Separate the factors in the denominator. | |
|
|
| Take the cube root of 8, which is 2. | |
|
|
| Rewrite the radical using a fractional exponent. | |
|
|
| Rewrite the fraction as a series of factors in order to cancel factors (see next step). | |
|
|
| Simplify the constant and c factors. | |
|
|
| Use the rule of negative exponents, n-x= | |
|
|
| Combine the b factors by adding the exponents. | |
|
|
| Change the expression with the fractional exponent back to radical form. By convention, an expression is not usually considered simplified if it has a fractional exponent or a radical in the denominator. | |
| Answer |
|
|
|
Well, that took a while, but you did it. You applied what you know about fractional exponents, negative exponents, and the rules of exponents to simplify the expression.
Summary
A radical can be expressed as an expression with a fractional exponent by following the convention ![]() . Rewriting radicals using fractional exponents can be useful in simplifying some radical expressions. When working with fractional exponents, remember that fractional exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.
. Rewriting radicals using fractional exponents can be useful in simplifying some radical expressions. When working with fractional exponents, remember that fractional exponents are subject to all of the same rules as other exponents when they appear in algebraic expressions.