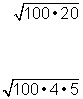Roots
Learning Objective(s)
· Find principal square roots and their opposites.
· Approximate square roots and find exact roots with a calculator.
Introduction
You have probably dealt with the roots of plants and trees when gardening, but did you know that there are roots in mathematics, too?
Yes, roots do exist in math. The most common root is the square root. Let’s take a look at what roots are, how they relate to exponents, and how you find the square root of a number.
To help understand square roots, let’s review some facts about exponents. Look at the table below.
| Exponent | Name | Expanded Form |
|
| “Three squared” “Three to the second power” |
|
|
| “Four to the fifth power” “Four to the fifth” |
|
|
| “x cubed” “x to the third power” “x to the third” |
|
|
| “x to the nth power” “x to the nth” |
|
You can think of exponential numbers as “repeated multiplication.”
Just as dividing is the inverse of multiplying, the inverse of raising a number to a power is taking the root of a number. The most common root (and the one you will be studying here) is called the square root. When you are trying to find the square root of a number (say, 25), you are trying to find a number that can be multiplied by itself to create that original number. In the case of 25, you can find that 5 • 5 = 25, so 5 must be the square root.
The symbol for the square root is called a radical symbol and looks like this: ![]() . The expression
. The expression ![]() is read “the square root of twenty-five” or “radical twenty-five.” The number that is written under the radical symbol is called the radicand. Take a look at the following table.
is read “the square root of twenty-five” or “radical twenty-five.” The number that is written under the radical symbol is called the radicand. Take a look at the following table.
| Radical | Name | Simplified Form |
|
| “Square root of thirty-six” “Radical thirty-six” |
|
|
| “Square root of one hundred” “Radical one hundred” |
|
|
| “Square root of two hundred twenty-five” “Radical two hundred twenty-five” |
|
Look at ![]() again. You may realize that there is another value that, when multiplied by itself, also results in 25. That number is −5.
again. You may realize that there is another value that, when multiplied by itself, also results in 25. That number is −5.
![]()
By definition, the square root symbol always means to find the positive root, called the principal root. So while 5 • 5 and −5 • −5 both equal 25, only 5 is the principal root. You should also know that zero is special because it has only one square root: itself (since 0 • 0 = 0).
If you know the principal square root, you can also find its opposite. (Recall that any number plus its opposite will equal 0. So, for instance,![]() .) In the table below, notice that while
.) In the table below, notice that while ![]() will give the principal root,
will give the principal root, ![]() will give its opposite. For example,
will give its opposite. For example, ![]() equals the principal square root, 6, and
equals the principal square root, 6, and ![]() equals its opposite, −6.
equals its opposite, −6.
| Radical | Principal Root | Opposite Radical | Opposite Root |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
There you have it—putting a negative sign in front of a radical has the effect of turning the principal root into its opposite (the negative square root of the radicand).
So now you have reviewed exponents, and you have been introduced to square roots. How does knowing about one help you understand the other?
Exponents and roots are connected—because roots can be expressed as fractional exponents. For now, let’s look at the connection between the exponent “![]() ” and square roots; you will learn about other fractional exponents and other roots later on. The square root of a number can be displayed by using the radical symbol or by raising the number to the
” and square roots; you will learn about other fractional exponents and other roots later on. The square root of a number can be displayed by using the radical symbol or by raising the number to the ![]() power. This is illustrated in the table below.
power. This is illustrated in the table below.
| Exponent Form | Root Form | Root of a Square | Simplified |
|
|
|
| 5 |
|
|
|
| 4 |
|
|
|
| 10 |
The square of 4 is 16 because 4 times 4 is equal to 16. Recall from your work with exponents that this can also be written as ![]() .
.
Thinking this way, you can identify that the square root of 9 is 3 because 3 • 3 = 9. Similarly, the square root of 25 is 5 because 5 • 5 = 25, and the square root of ![]() is x since
is x since ![]() . For example,
. For example, ![]() . (You will often see this type of notation—where you take the square root of a squared number—when you simplify, multiply, and divide radicals.)
. (You will often see this type of notation—where you take the square root of a squared number—when you simplify, multiply, and divide radicals.)
Simplifying Square Roots
Ok…square roots and exponents are connected. Keep that in mind as you begin simplifying some square roots.
This first example, “Simplify ![]() ,” can be read “Simplify the square root of 144.” Think about a number that, when multiplied by itself, has a product of 144.
,” can be read “Simplify the square root of 144.” Think about a number that, when multiplied by itself, has a product of 144.
| Example | ||
| Problem | Simplify. |
|
|
|
| Determine what number multiplied by itself has a product of 144. |
|
| 12 | The square root of 144 is 12. |
| Answer |
|
|
| Example | ||
| Problem | Simplify. |
|
|
|
| The radical symbol acts like a grouping sign.
The negative in front means to take the opposite of the value after you simplify the radical. |
|
| −(9) | The square root of 81 is 9. Then, take the opposite of 9. |
| Answer |
|
|
However, if the negative sign is under the radical as in ![]() , there is no way to simplify it using real numbers. That is because there is no number that you could multiply by itself to get −49. Remember, a negative number multiplied by a negative number results in a positive number: −7 • −7 = 49.
, there is no way to simplify it using real numbers. That is because there is no number that you could multiply by itself to get −49. Remember, a negative number multiplied by a negative number results in a positive number: −7 • −7 = 49.
If finding the square root by trial and error is difficult, you can use what you know about factoring to help you determine the principal root.
| Example | ||
| Problem | Simplify. |
|
|
|
| Determine the prime factors of 144.
|
|
|
| Regroup these factors into two identical groups.
Recall that the square root of a squared number is the number itself. Here, |
| Answer |
|
|
Notice something that happened in the final step of this example: the expression ![]() was rewritten as
was rewritten as ![]() , and then
, and then ![]() . You split the factors into identical groupings, multiplied them, and arrived at a squared number.
. You split the factors into identical groupings, multiplied them, and arrived at a squared number.
Many times, though, it is easier to identify factor pairs after you have gone through the process of factoring the original radical. For example, look at ![]() again. How many pairs of
again. How many pairs of ![]() do you see? What about
do you see? What about ![]() ? If you could somehow identify smaller squared numbers underneath the radical instead of recombining all the factors (as you did when you found that
? If you could somehow identify smaller squared numbers underneath the radical instead of recombining all the factors (as you did when you found that ![]() ), you might be able to simplify radicals more quickly.
), you might be able to simplify radicals more quickly.
This is where it helps to think of roots as fractional exponents. Recall the Product Raised to a Power Rule from when you studied exponents. This rule states that the product of two or more non-zero numbers raised to a power is equal to the product of each number raised to the same power. In math terms, it is written (ab)x = ax • bx. So, for example, you can use the rule to rewrite ![]() as
as ![]() .
.
Now instead of using the exponent 2, let’s use the exponent ![]() . The exponent is distributed in the same way.
. The exponent is distributed in the same way.
![]()
And since you know that raising a number to the ![]() power is the same as taking the square root of that number, you can also write it this way.
power is the same as taking the square root of that number, you can also write it this way.
![]()
Look at that—you can think of any number underneath a radical as the product of separate factors, each underneath its own radical. Using this idea helps you identify smaller squared numbers, which often lets you simplify radicals more quickly.
| A Product Raised to a Power Rule or sometimes called The Square Root of a Product Rule
For any numbers a and b,
For example:
|
This rule is important because it helps you think of one radical as the product of multiple radicals. If you can identify perfect squares within a radical, as with ![]() , you can rewrite the expression as the product of multiple perfect squares:
, you can rewrite the expression as the product of multiple perfect squares: ![]() . Let’s take another look at
. Let’s take another look at ![]() using this new idea.
using this new idea.
| Example | ||
| Problem | Simplify. |
|
|
|
| Determine the prime factors of 144. |
|
|
| Group like factors into pairs. |
|
|
| Rewrite as squares. |
|
|
| Using the Product Raised to a Power rule, rewrite as a product of individual radicals. |
|
|
| Simplify each radical, then multiply. |
| Answer |
|
|
You get the same solution in both cases, but it is often easier to pull out smaller factor pairs and then multiply them together (as shown here) than recombining all the factors to find the full root (as shown in the first example).
| Simplify.
A) 16
B) 18
C) 21
D) 162
|
Simplifying Square Roots by Factoring
So far, you have seen examples that are perfect squares. That is, each is a number whose square root is an integer. But many radical expressions are not perfect squares. Some of these radicals can still be simplified by finding perfect square factors. The example below illustrates how to factor the radicand, looking for pairs of factors that can be expressed as a power.
| Example | |||
| Problem | Simplify. |
| |
|
|
| Factor 63 into 7 and 9. | |
|
|
| Factor 9 further into 3 and 3. | |
|
|
| Rewrite 3 · 3 as 32. | |
|
|
| Using the Product Raised to a Power rule, separate the radical into the product of two factors, each under a radical. | |
|
|
| Take the square root of 32. | |
|
|
| Rearrange factors so the integer appears before the radical, and then multiply. (This is done so that it is clear that only the 7 is under the radical, not the 3.) | |
| Answer |
|
| |
The final answer ![]() may look a bit odd, but it is in simplified form. You can read this as “three radical seven” or “three times the square root of seven.”
may look a bit odd, but it is in simplified form. You can read this as “three radical seven” or “three times the square root of seven.”
| Example | ||
| Problem | Simplify. |
|
|
|
| Factor 2,000 to find perfect squares.
Continue factoring until all perfect squares are identified. |
|
|
| Factor 100 as 10 • 10 and 4 as 2 • 2. |
|
|
| Rewrite 10 • 10 as 102 and 2 • 2 as 22. |
|
|
| Using the Product Raised to a Power rule, rewrite the radical as the product of three factors, each under a radical. |
|
|
| Take the square root of 102 and 22. |
|
|
| Multiply. |
| Answer |
|
|
Another approach to handling square roots that are not perfect squares is to approximate them by comparing the values to perfect squares. Suppose you wanted to know the square root of 17. Let’s look at how you might approximate it.
| Example | ||
| Problem | Simplify. |
|
|
| 17 is in between the perfect squares 16 and 25. So, | Think of two perfect squares that surround 17. |
|
|
Since 17 is closer to 16 than 25,
| Determine whether |
|
| 4.1 • 4.1 = 16.81
4.2 • 4.2 = 17.64 | Use trial and error to get a better estimate of
(4.1)2 gives a closer estimate than (4.2)2. |
|
| 4.12 • 4.12 = 16.9744
4.13 • 4.13 = 17.0569 | Continue to use trial and error to get an even better estimate. |
| Answer |
|
|
This approximation is pretty close. If you kept using this trial and error strategy you could continue to find the square root to the thousandths, ten-thousandths, and hundred-thousandths places, but eventually it would become too tedious to do by hand.
For this reason, when you need to find a more precise approximation of a square root, you should use a calculator. Most calculators have a square root key ![]() that will give you the square root approximation quickly. On a simple 4-function calculator, you would likely key in the number that you want to take the square root of and then press the square root key.
that will give you the square root approximation quickly. On a simple 4-function calculator, you would likely key in the number that you want to take the square root of and then press the square root key.
Try to find ![]() using your calculator. Note that you will not be able to get an “exact” answer because
using your calculator. Note that you will not be able to get an “exact” answer because ![]() is an irrational number, a number that cannot be expressed as a fraction, and the decimal never terminates or repeats. To nine decimal positions,
is an irrational number, a number that cannot be expressed as a fraction, and the decimal never terminates or repeats. To nine decimal positions, ![]() is approximated as 4.123105626. A calculator can save a lot of time and yield a more precise square root when you are dealing with numbers that aren’t perfect squares.
is approximated as 4.123105626. A calculator can save a lot of time and yield a more precise square root when you are dealing with numbers that aren’t perfect squares.
| Example | ||
| Problem | Approximate | |
|
| 50 is in between the perfect squares 49 and 64.
| Find the perfect squares that surround 50. |
|
| 49 and 50 are close, so
7.1 • 7.1 = 50.41
Since 50.41 is greater than 50, the estimate must be between 7 and 7.1. | Using number sense and trial and error, try squaring incrementally greater numbers, beginning with 7.1, to find a good approximation for |
|
| Since 50 is closer to 50.41 than to 49, try 7.07.
7.07 • 7.07 = 49.9849 | Use reasoning to get an estimate to the hundredths place. |
|
|
| Use a calculator. |
| Answer | By approximation: Using a calculator: |
|
Summary
The square root of a number is the number which, when multiplied by itself, gives the original number. Principal square roots are always positive and the square root of 0 is 0. You can only take the square root of values that are greater than or equal to 0. The square root of a perfect square will be an integer. Other square roots can be simplified by identifying factors that are perfect squares and taking their square root. Square roots can be approximated using trial and error or a calculator.