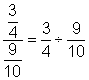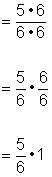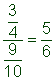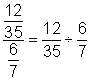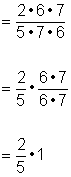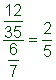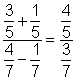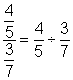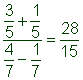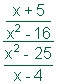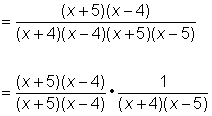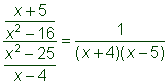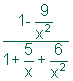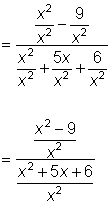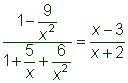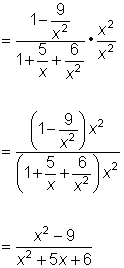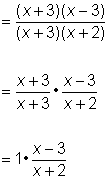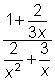Complex Rational Expressions
Learning Objective(s)
· Simplify complex rational expressions.
Introduction
Fractions and rational expressions can be interpreted as quotients. When both the dividend (numerator) and divisor (denominator) include fractions or rational expressions, you have something more complex than usual. Don’t fear—you have all the tools you need to simplify these quotients!
Complex Fractions
A complex fraction is the quotient of two fractions. These complex fractions are never considered to be in simplest form, but they can always be simplified using division of fractions.
| Example | ||
| Problem | Simplify.
|
|
|
|
| Rewrite the complex fraction as a division problem. |
|
|
| Rewrite the division as multiplication, using the reciprocal of the divisor. |
|
|
| Multiply, and simplify if possible. |
| Answer |
|
|
Before you multiply the numbers, it’s often helpful to factor the numbers. You can then use the factors to create a fraction equal to 1.
| Example | ||
| Problem | Simplify.
|
|
|
|
| Rewrite the complex fraction as a division problem. |
|
|
| Rewrite the division as multiplication, using the reciprocal of the divisor. |
|
|
| Factor the numerator and denominator, looking for common factors, before multiplying numbers together. |
| Answer |
|
|
If two fractions appear in the numerator or denominator (or both), first combine them. Then simplify the quotient as shown above.
| Example | ||
| Problem | Simplify.
|
|
|
|
| First combine the numerator and denominator by adding or subtracting. |
|
|
| Rewrite the complex fraction as a division problem. |
|
|
| Rewrite the division as multiplication, using the reciprocal of the divisor. |
|
|
| Multiply and simplify as needed. |
| Answer |
|
|
| Simplify.
A)
B)
C)
D)
|
A complex rational expression is a quotient with rational expressions in the dividend, divisor, or in both. Simplify these in the exact same way as you would a complex fraction.
| Example | ||
| Problem | Simplify.
|
|
|
|
| Rewrite the complex rational expression as a division problem. |
|
|
| Rewrite the division as multiplication, using the reciprocal of the divisor. Note that the excluded values for this are -4, 4 and 5, because those values make the denominators of one of the fractions zero. |
|
|
| Factor the numerator and denominator, looking for common factors. In this case, x + 5 and x – 4 are common factors of the numerator and denominator. Notice that |
| Answer |
|
|
The same ideas can be used when simplifying complex rational expressions that include more than one rational expression in the numerator or denominator. However, there is a shortcut that can be used. Compare these two examples of simplifying a complex fraction.
| Example | ||
| Problem | Simplify.
|
|
|
| Combine the expressions in the numerator and denominator. To do this, rewrite the expressions using a common denominator. There is an excluded value of 0 because this makes the denominators of the fractions zero. | |
|
| Rewrite the complex rational expression as a division problem. (When you are comfortable with the step of rewriting the complex rational fraction as a division problem, you might skip this step and go straight to rewriting it as multiplication.) | |
|
| Rewrite the division as multiplication, using the reciprocal of the divisor. | |
|
| Factor the numerator and denominator, looking for common factors. In this case, x + 3 and x2 are common factors. We can now see there are two additional excluded values, -2 and -3. | |
| Answer |
|
|
| Example | ||
| Problem | Simplify.
|
|
|
|
| Before combining the expressions, find a common denominator for all of the rational expressions. (In this case, x2 is a common denominator.) Multiply by 1 in the form of a fraction with the common denominator in both numerator and denominator. (In this case, multiply by |
|
|
| Notice that the expression is no longer complex! You can simplify by factoring and identifying common factors. We can now see there are two additional excluded values, -2 and -3. |
| Answer |
|
|
You may find the second method easier to use. Try both methods on the following problem.
| Simplify.
A) 1
B)
C)
D)
|
Summary
Complex rational expressions are quotients with rational expressions in the divisor, dividend, or both. When written in fractional form, they appear to be fractions within a fraction. These can be simplified by first treating the quotient as a division problem. Then you can rewrite the division as multiplication using the reciprocal of the divisor. Or you can simplify the complex rational expression by multiplying both the numerator and denominator by a denominator common to all rational expressions within the complex expression. This can help simplify the complex expression even faster.