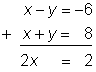The Elimination Method
Learning Objective(s)
· Solve a system of equations when no multiplication is necessary to eliminate a variable.
· Solve a system of equations when multiplication is necessary to eliminate a variable.
· Recognize systems that have no solution or an infinite number of solutions.
· Solve application problems using the elimination method.
Introduction
The elimination method for solving systems of linear equations uses the addition property of equality. You can add the same value to each side of an equation.
So if you have a system: x – 6 = −6 and x + y = 8, you can add x + y to the left side of the first equation and add 8 to the right side of the equation. And since x + y = 8, you are adding the same value to each side of the first equation.
If you add the two equations, x – y = −6 and x + y = 8 together, as noted above, watch what happens.
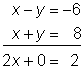
You have eliminated the y term, and this equation can be solved using the methods for solving equations with one variable.
Let’s see how this system is solved using the elimination method.
| Example | ||||
| Problem | Use elimination to solve the system. x – y = −6 x + y = 8 |
| ||
|
|
| Add the equations. | ||
|
| 2x = 2 x = 1 | Solve for x. | ||
|
| x + y = 8 1 + y = 8 y = 8 – 1 y = 7 | Substitute x = 1 into one of the original equations and solve for y. | ||
|
| x – y = −6 1 – 7 = −6 −6 = −6
TRUE | x + y = 8 1 + 7 = 8 8 = 8
TRUE | Be sure to check your answer in both equations!
The answers check. | |
| Answer | The solution is (1, 7). |
| ||
Unfortunately not all systems work out this easily. How about a system like 2x + y = 12 and −3x + y = 2. If you add these two equations together, no variables are eliminated.
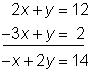
But you want to eliminate a variable. So let’s add the opposite of one of the equations to the other equation.
2x + y =12 → 2x + y = 12 → 2x + y = 12
−3x + y = 2 → − (−3x + y) = −(2) → 3x – y = −2
5x + 0y = 10
You have eliminated the y variable, and the problem can now be solved. See the example below.
| Example | ||||
| Problem | Use elimination to solve the system. 2x + y = 12 −3x + y = 2 |
| ||
|
| 2x + y = 12 −3x + y = 2 | You can eliminate the y-variable if you add the opposite of one of the equations to the other equation. | ||
|
| 2x + y = 12 3x – y = −2 5x = 10 | Rewrite the second equation as its opposite. Add. | ||
|
| x = 2 | Solve for x. | ||
|
| 2(2) + y = 12 4 + y = 12 y = 8 | Substitute y = 2 into one of the original equations and solve for y. | ||
|
| 2x + y = 12 2(2) + 8 = 12 4 + 8 = 12 12 = 12
TRUE | −3x + y = 2 −3(2) + 8 = 2 −6 + 8 = 2 2 = 2
TRUE | Be sure to check your answer in both equations!
The answers check. | |
| Answer | The solution is (2, 8). |
| ||
The following are two more examples showing how to solve linear systems of equations using elimination.
| Example | |||||||||||||||||||||||||||||||||||
| Problem | Use elimination to solve the system. −2x + 3y = −1 2x + 5y = 25 | ||||||||||||||||||||||||||||||||||
|
|
| Notice the coefficients of each variable in each equation. If you add these two equations, the x term will be eliminated since −2x + 2x = 0. | |||||||||||||||||||||||||||||||||
|
|
| Add and solve for y. | |||||||||||||||||||||||||||||||||
|
| 2x + 5y = 25 2x + 5(3) = 25 2x + 15 = 25 2x = 10 x = 5 | Substitute y = 3 into one of the original equations. | |||||||||||||||||||||||||||||||||
|
| −2x + 3y = −1 −2(5) + 3(3) = −1 −10 + 9 = −1 −1 = −1
TRUE | 2x + 5y = 25 2(5) + 5(3) = 25 10 + 15 = 25 25 = 25
TRUE | Check solutions.
The answers check. | ||||||||||||||||||||||||||||||||
| Answer | The solution is (5, 3). |
| |||||||||||||||||||||||||||||||||
| Example | ||||||||||||||||||||||||||||
| Problem | Use elimination to solve for x and y. 4x + 2y = 14 5x + 2y = 16 |
| ||||||||||||||||||||||||||
|
|
| Notice the coefficients of each variable in each equation. You will need to add the opposite of one of the equations to eliminate the variable y, as 2y + 2y = 4y, but 2y + (−2y) = 0. | ||||||||||||||||||||||||||
|
|
| Change one of the equations to its opposite, add and solve for x.
| ||||||||||||||||||||||||||
|
| 4x + 2y = 14 4(2) + 2y = 14 8 + 2y = 14 2y = 6 y = 3 | Substitute x = 2 into one of the original equations and solve for y. | ||||||||||||||||||||||||||
| Answer | The solution is (2, 3). |
| ||||||||||||||||||||||||||
Go ahead and check this last example—substitute (2, 3) into both equations. You get two true statements: 14 = 14 and 16 = 16!
Notice that you could have used the opposite of the first equation rather than the second equation and gotten the same result.
Many times adding the equations or adding the opposite of one of the equations will not result in eliminating a variable. Look at the system below.
3x + 4y = 52
5x + y = 30
If you add the equations above, or add the opposite of one of the equations, you will get an equation that still has two variables. So let’s now use the multiplication property of equality first. You can multiply both sides of one of the equations by a number that will result in the coefficient of one of the variables being the opposite of the same variable in the other equation.
This is where multiplication comes in handy. Notice that the first equation contains the term 4y, and the second equation contains the term y. If you multiply the second equation by −4, when you add both equations the y variables will add up to 0.
3x + 4y = 52 → 3x + 4y = 52 → 3x + 4y = 52
5x + y = 30 → −4(5x + y) = −4(30) → −20x – 4y = −120
−17x + 0y = −68
See the example below.
| Example | |||||||||||||||||||
| Problem | Solve for x and y. Equation A: 3x + 4y = 52 Equation B: 5x + y = 30 | ||||||||||||||||||
|
|
| Look for terms that can be eliminated. The equations do not have any x or y terms with the same coefficients.
| |||||||||||||||||
|
|
| Multiply the second equation by −4 so they do have the same coefficient. | |||||||||||||||||
|
|
| Rewrite the system, and add the equations. | |||||||||||||||||
|
|
| Solve for x. | |||||||||||||||||
|
| 3x + 4y = 52 3(4) + 4y = 52 12 + 4y = 52 4y = 40 y = 10 | Substitute x = 4 into one of the original equations to find y. | |||||||||||||||||
|
| 3x + 4y = 52 3(4) + 4(10) = 52 12 + 40 = 52 52 = 52
TRUE | 5x + y = 30 5(4) + 10 = 30 20 + 10 = 30 30 = 30
TRUE | Check your answer.
The answers check. | ||||||||||||||||
| Answer | The solution is (4, 10). |
| |||||||||||||||||
There are other ways to solve this system. Instead of multiplying one equation in order to eliminate a variable when the equations were added, you could have multiplied both equations by different numbers.
Let’s remove the variable x this time. Multiply Equation A by 5 and Equation B by −3.
| Example | |||||||||||||||||||||||||||||||
| Problem | Solve for x and y. 3x + 4y = 52 5x + y = 30 |
| |||||||||||||||||||||||||||||
|
|
| Look for terms that can be eliminated. The equations do not have any x or y terms with the same coefficient.
| |||||||||||||||||||||||||||||
|
|
| In order to use the elimination method, you have to create variables that have the same coefficient—then you can eliminate them. Multiply the top equation by 5. | |||||||||||||||||||||||||||||
|
|
| Now multiply the bottom equation by −3. | |||||||||||||||||||||||||||||
|
|
| Next add the equations, and solve for y. | |||||||||||||||||||||||||||||
|
| 3x + 4y = 52 3x + 4(10) = 52 3x + 40 = 52 3x = 12 x = 4 | Substitute y = 10 into one of the original equations to find x. | |||||||||||||||||||||||||||||
| Answer | The solution is (4, 10). | You arrive at the same solution as before. | |||||||||||||||||||||||||||||
These equations were multiplied by 5 and −3 respectively, because that gave you terms that would add up to 0. Be sure to multiply all of the terms of the equation.
| Felix needs to find x and y in the following system. Equation A: 7y − 4x = 5 Equation B: 3y + 4x = 25
If he wants to use the elimination method to eliminate one of the variables, which is the most efficient way for him to do so?
A) Add Equation A and Equation B
B) Add 4x to both sides of Equation A
C) Multiply Equation A by 5
D) Multiply Equation B by −1
|
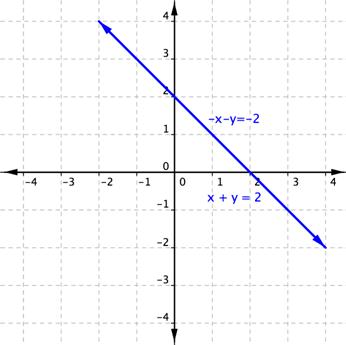
Just as with the substitution method, the elimination method will sometimes eliminate both variables, and you end up with either a true statement or a false statement. Recall that a false statement means that there is no solution.
Let’s look at an example.
| Example | ||
| Problem | Solve for x and y. -x – y = -4 x + y = 2 |
|
|
| -x – y = -4 x + y = 2 0 = −2 | Add the equations to eliminate the x-term. |
| Answer | There is no solution. |
|
Graphing these lines shows that they are parallel lines and as such do not share any point in common, verifying that there is no solution.
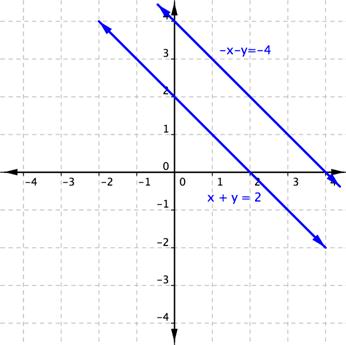
If both variables are eliminated and you are left with a true statement, this indicates that there are an infinite number of ordered pairs that satisfy both of the equations. In fact, the equations are the same line.
| Example | ||
| Problem | Solve for x and y. x + y = 2 -x − y = -2 |
|
| x + y = 2 -x − y = -2 0 = 0 | Add the equations to eliminate the x-term. | |
| Answer | There are an infinite number of solutions. | |
Graphing these two equations will help to illustrate what is happening.
The elimination method can be applied to solving systems of equations that model real situations. Two examples of using the elimination method in problem solving are shown below.
| Example | |||
| Problem | The sum of two numbers is 10. Their difference is 6. What are the two numbers? | ||
|
| x + y = 10 x – y = 6 | Write a system of equations to model the situation. x = one number y = the other number | |
|
| x + y = 10 + x – y = 6 2x = 16 x = 8 | Add the equations to eliminate the y-term and then solve for x. | |
|
| x + y = 10 8 + y = 10 y = 2 | Substitute the value for x into one of the original equations to find y. | |
|
| x + y = 10 8 + 2 = 10 10 = 10
TRUE | x – y = 6 8 – 2 = 6 6 = 6
TRUE | Check your answer by substituting x = 8 and y = 2 into the original system.
The answers check. |
| Answer | The numbers are 8 and 2. | ||
| Example | ||||
| Problem | A theater sold 800 tickets for Friday night’s performance. One child ticket costs $4.50 and one adult ticket costs $6.00.The total amount collected was $4,500. How many of each type of ticket were sold? | |||
|
| The total number of tickets sold is 800. a + c = 800 The amount of money collected is $4,500 6a + 4.5c = 4,500
System of equations: a + c = 800 6a + 4.5c = 4,500 | Write a system of equations to model the ticket sale situation. a = number of adult tickets sold c = number of child tickets sold | ||
|
| 6(a + c) = 6(800) 6a + 4.5c = 4,500
6a + 6c = 4,800 6a + 4.5c = 4,500 | Use multiplication to re-write the first equation.
| ||
|
| 6a + 6c = 4,800 −6a – 4.5c = −4,500 1.5c = 300
c = 200 | Add the opposite of the second equation to eliminate a term and solve for c. | ||
|
| a + 200 = 800 −200 −200 a = 600 | Substitute 200 in for c in one of the original equations. | ||
|
| a + c = 800 600 + 200 = 800 800 = 800
TRUE
| 6a + 4.5c = 4,500 6(600) + 4.5(200) = 4,500 3,600 + 900 = 4,500 4500 = 4,500
TRUE | Check your answer by substituting a = 600 and c = 200 into the original system. The answers check. | |
| Answer | 600 adult tickets and 200 child tickets were sold. |
| ||
Summary
Combining equations is a powerful tool for solving a system of equations. Adding or subtracting two equations in order to eliminate a common variable is called the elimination (or addition) method. Once one variable is eliminated, it becomes much easier to solve for the other one. Multiplication can be used to set up matching terms in equations before they are combined. When using the multiplication method, it is important to multiply all the terms on both sides of the equation—not just the one term you are trying to eliminate.