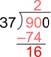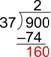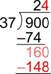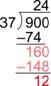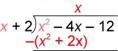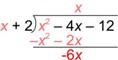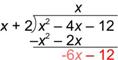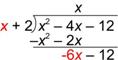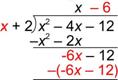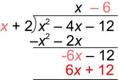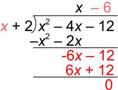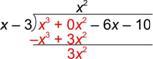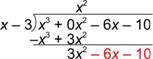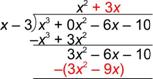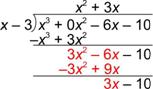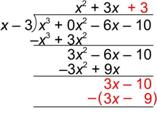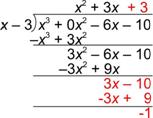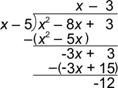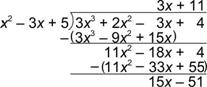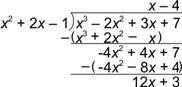Dividing by Binomials and Polynomials
Learning Objective(s)
· Divide a polynomial by a binomial.
· Divide a polynomial by another polynomial.
Introduction
Dividing a polynomial by a monomial can be handled by dividing each term in the polynomial separately. This can’t be done when the divisor has more than one term. However, the process of long division can be very helpful with polynomials.
First, recall how you can use long division to divide two whole numbers, say 900 divided by 37.
|
| First, you would think about how many 37s are in 90, as 9 is too small. (Note: you could also think, how many 40s are there in 90.) |
|
| There are two 37s in 90, so write 2 above the last digit of 90. Two 37s is 74; write that product below the 90. |
|
| Subtract: 90 – 74 is 16. (If the result is larger than the divisor, 37, then you need to use a larger number for the quotient.) |
|
| Bring down the next digit (0) and consider how many 37s are in 160. |
|
| There are four 37s in 160, so write the 4 next to the two in the quotient. Four 37s is 148; write that product below the 160. |
|
| Subtract: 160 – 148 is 12. This is less than 37 so the 4 is correct. Since there are no more digits in the dividend to bring down, you’re done. |
The final answer is 24 R12, or ![]() . You can check this by multiplying the quotient (without the remainder) by the divisor, and then adding in the remainder. The result should be the dividend:
. You can check this by multiplying the quotient (without the remainder) by the divisor, and then adding in the remainder. The result should be the dividend:
24 • 37 + 12 = 888 + 12 = 900
To divide polynomials, use the same process. This example shows how to do this when dividing by a binomial.
| Example | |||
| Problem | Divide: (x2 – 4x – 12) ¸ (x + 2) | ||
|
|
|
| How many x’s are there in x2? That is, what is |
|
|
|
|
Write the product of the divisor and the part of the quotient you just found under the dividend. Since x(x + 2) = x2 + 2x, write this underneath, and get ready to subtract.
|
|
|
|
| Rewrite –(x2 + 2x) as its opposite –x2 – 2x so that you can add the opposite. (Adding the opposite is the same as subtracting, and it is easier to do.) |
|
|
|
|
Add -x2 to x2, and -2x to -4x. |
|
|
|
| Bring down -12. |
|
|
|
| Repeat the process. How many times does x go into -6x? In other words, what is |
|
|
|
| Since |
|
|
|
| Rewrite –(-6x – 12) as 6x + 12, so that you can add the opposite. |
|
|
|
| Add. In this case, there is no remainder, so you’re done. |
| Answer | (x2 – 4x – 12) ¸ (x + 2) = x – 6 |
|
|
Check this by multiplying:
(x – 6)(x + 2) = x2 + 2x – 6x – 12 = x2 – 4x – 12
Let’s try another example. In this example, a term is “missing” from the dividend.
| Example | |||
| Problem | Divide: (x3 – 6x – 10) ¸ (x – 3) | ||
|
|
|
| In setting up this problem, notice that there is an x3 term but no x2 term. Add 0x2 as a “place holder” for this term. (Since 0 times anything is 0, you’re not changing the value of the dividend.) |
|
|
|
| Focus on the first terms again: how many x’s are there in x3? Since
Multiply x2(x – 3) = x3 – 3x2, write this underneath the dividend and prepare to subtract. |
|
|
|
| Rewrite the subtraction using the opposite of the expression x3 – 3x2. Then add. |
|
|
|
| Bring down the rest of the expression in the dividend. It’s helpful to bring down all of the remaining terms. |
|
|
|
| Now, repeat the process with the remaining expression, 3x2 – 6x – 10, as the dividend. |
|
|
|
| Remember to watch the signs! |
|
|
|
| How many x’s are there in 3x? Since there are 3, multiply 3(x – 3) = 3x – 9, write this underneath the dividend and prepare to subtract. |
|
|
|
| Continue until the degree of the remainder is less than the degree of the divisor. In this case the degree of the remainder, -1, is 0, which is less than the degree of x – 3, which is 1.
Also notice that you have brought down all the terms in the dividend, and that the quotient extends to the right edge of the dividend. These are other ways to check whether you have completed the problem. |
| Answer | (x3 – 6x – 10) ¸ (x – 3) = x2 + 3x + 3 R -1, x2 + 3x + 3 + x2 + 3x + 3 – |
| You can write the remainder using the symbol R, or as a fraction added to the rest of the quotient with the remainder in the numerator and the divisor in the denominator. In this case, since the remainder is negative, you can also subtract the opposite. |
Check the result:
| (x – 3)(x2 + 3x + 3) | = | x(x2 + 3x + 3) – 3(x2 + 3x + 3) |
|
| = | x3 + 3x2 + 3x – 3x2 – 9x – 9 |
|
| = | x3 – 6x – 9 |
|
|
|
|
| x3 – 6x – 9 + (-1) | = | x3 – 6x – 10 |
| Divide: (x2 – 8x + 3) ¸ (x – 5)
A) x – 3 –
B) x – 13 +
C) x – 13 –
D) x – 15
|
The process above works for dividing any polynomials, no matter how many terms are in the divisor or the dividend. The main things to remember are:
· When subtracting, be sure to subtract the whole expression, not just the first term. This is very easy to forget, so be careful!
· Stop when the degree of the remainder is less than the degree of the dividend, or when you have brought down all the terms in the dividend, and that the quotient extends to the right edge of the dividend.
| Example | |||
| Problem | Divide: (3x3 + 2x2 – 3x + 4) ¸ (x2 – 3x + 5) | ||
|
|
|
| Focus on the first terms: What is
The degree of the remainder is 1, which is less than the degree of the divisor, 2. You can stop. |
| Answer | (3x3 + 2x2 – 3x + 4) ¸ (x2 – 3x + 5) = 3x + 11 R 15x – 51, or 3x + 11 + |
|
|
Check:
| (x2 – 3x + 5)(3x + 11) | = | (x2 – 3x + 5)(3x) + (x2 – 3x + 5)(11) |
|
| = | 3x3 – 9x2 + 15x + 11x2 – 33x + 55 |
|
| = | 3x3 + 2x2 – 18x + 55 |
|
|
|
|
| 3x3 + 2x2 – 18x + 55 + (15x – 51) | = | 3x3 + 2x2 – 3x + 4 |
| Divide: (x3 – 2x2 + 3x + 7) ¸ (x2 + 2x – 1)
A) x +
B) x + 8 +
C) x – 4 +
D) 13x – 1
|
Summary
Dividing polynomials by polynomials of more than one term can be done using a process very much like long division of whole numbers. You must be careful to subtract entire expressions, not just the first term. Stop when the degree of the remainder is less than the degree of the divisor. The remainder can be written using R notation, or as a fraction added to the quotient with the remainder in the numerator and the divisor in the denominator.