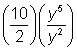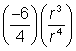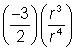Dividing by a Monomial

 

Learning Objective(s)

·         Divide a monomial by a monomial.

·         Divide a polynomial by a monomial.

 

Introduction

 

The fourth arithmetic operation is division, the inverse of multiplication. Division of polynomials isn’t much different from division of numbers. Let’s start with dividing a monomial by another monomial, which is the basis for dividing a polynomial by a monomial.

 

Dividing Monomials by Monomials

 

When you multiply two monomials, you multiply the coefficients together and then you multiply the variables together. Similarly, when dividing monomials, you divide the coefficients and then divide variables. When there are exponents with the same base, the law of exponents says you divide by subtracting the exponents. Consider this example:

 

 

Example

Problem

 

 

 

Group the monomial into numerical and variable factors.

 

 

Divide the coefficients, and divide the variables by subtracting the exponents of each y term.

Answer

 =

 

 

 

Here’s another example:

 

 

Example

Problem

A rectangle has an area of 8x2 and a length of 4x. Find the width of the rectangle using the formula: .

 

Substitute known values.

 

Divide coefficients, and divide the variables by subtracting the exponents of each x term.

 

 

 

Answer

width =  units

 

 

 

Sometimes division requires simplification.

 

 

Example

Problem

Divide.

 

 

Group the monomial into numerical and variable factors.

 

 

Simplify to .

 

Divide the variables by subtracting the exponents of r. Note that the variable has a negative exponent.

 

Simplify  by rewriting it as the inverse of r.

 

Multiply.

Answer

 =

 

 

 

Remember that a term is not considered simplified if it contains a negative exponent; this is why  was rewritten as .

 

 

Divide:

 

A) 11x4

 

B) 22x3

 

C) 11x3

 

D) 22x4

 

Show/Hide Answer

A) 11x4

Incorrect. You divided 22 by 2, but you must subtract the exponents of the variable x. Since x = x1, this is x4 – 1 = x3. The correct answer is 11x3.

 

B) 22x3

Incorrect. You correctly divided the variables, but you must also divide 22 by 2. The correct answer is 11x3.

 

C) 11x3

Correct.  = 11 and x4 – 1 = x3 so the correct answer is 11x3.

 

D) 22x4

Incorrect. Divide the coefficients to get  = 11 for the coefficient. Divide the variables by subtracting the exponents. Since x = x1, this is x4 – 1 = x3. The correct answer is 11x3.

 

 

 

Dividing Polynomials by Monomials

 

The distributive property states that you can distribute a factor that is being multiplied by a sum or difference, and likewise you can distribute a divisor that is being divided into a sum or difference (as division can be changed to multiplication.)

 

 

Or you can distribute the 2, and divide each term by 2.

 

 

Let’s try something similar with a polynomial.

 

 

Example

Problem

Divide.

 

 

 

Distribute 2x over the polynomial by dividing each term by 2x.

 

Divide each term, a monomial divided by another monomial.

Answer

 =

 

 

 

Let’s try one more example, watch the signs.

 

 

Example

Problem

Divide.

 

 

Divide each term in the polynomial by the monomial.

 

 

Simplify. Remember that 18 can be written as 18y0. So the exponents are  0 – 1 = −1.

 

Write the final answer without any negative exponents.

Answer

 =

 

 

 

Divide:

 

A)

 

B)

 

C)

 

D)

 

 

Show/Hide Answer

A)

Correct. Divide each term in the polynomial by the monomial: , which gives .

 

B)

Incorrect. You only divided the first term. Divide each term in the polynomial by the monomial: . The correct answer is .

 

 

C)

Incorrect. You removed the two t2 terms, but did not divide. Divide each term in the polynomial by the monomial: . The correct answer is .

 

D)

Incorrect. Divide each term in the polynomial by the monomial: The correct answer is .

 

 

 

Summary

 

To divide a monomial by a monomial, divide the coefficients (or simplify them as you would a fraction) and divide the variables with like bases by subtracting their exponents. To divide a polynomial by a monomial, divide each term of the polynomial by the monomial. Be sure to watch the signs! Final answers should be written without any negative exponents.