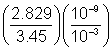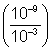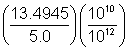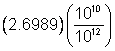Scientific Notation
Learning Objective(s)
· Convert between scientific and decimal notation.
· Multiply and divide using scientific notation.
· Solve application problems.
Introduction
When working with very large or very small numbers, scientists, mathematicians, and engineers often use scientific notation to express those quantities. Scientific notation uses exponential notation. The following are examples of scientific notation.
Light year: number of miles light travels in one year, about 5,880,000,000,000
Scientific notation is 5.88 x 1012 miles.
hydrogen atom: has a diameter of about 0.00000005 mm
Scientific notation is 5 x 10-8 mm
Computation with very large numbers is made easier with scientific notation.
Learning to Use Scientific Notation
When a number is written in scientific notation, the exponent tells you if the term is a large or a small number. A positive exponent indicates a large number and a negative exponent indicates a small number that is between 0 and 1.
Since it’s so useful, let’s look more closely at the details of scientific notation format.
| Scientific Notation A positive number is written in scientific notation if it is written as a x 10n where the coefficient a has a value such that 1 ≤ a < 10 and n is an integer. |
Look at the numbers below. Which of the numbers is written in scientific notation?
| Number | Scientific Notation? | Explanation |
| 1.85 x 10-2 | yes | 1 ≤1.85 < 10
-2 is an integer |
|
| no |
|
| 0.82 x 1014 | no | 0.82 is not ≥ 1 |
| 10 x 103 | no | 10 is not < 10 |
| Which number below is written in scientific notation?
A) 4.25 x 100.08
B) 0.425 x 107
C) 42.5 x 105
D) 4.25 x 106
|
Writing Decimal Notation in Scientific Notation
Now let’s compare some numbers expressed in both scientific notation and standard decimal notation in order to understand how to convert from one form to the other. Take a look at the tables below. Pay close attention to the exponent in the scientific notation and the position of the decimal point in the decimal notation.
| Large Numbers |
| Small Numbers | ||
| Decimal Notation | Scientific Notation |
| Decimal Notation | Scientific Notation |
| 500.0 | 5 x 102 |
| 0.05 | 5 x 10-2 |
| 80,000.0 | 8 x 104 |
| 0.0008 | 8 x 10-4 |
| 43,000,000.0 | 4.3 x 107 |
| 0.00000043 | 4.3 x 10-7 |
| 62,500,000,000.0 | 6.25 x 1010 |
| 0.000000000625 | 6.25 x 10-10 |
To write a large number in scientific notation, move the decimal point to the left to obtain a number between 1 and 10. Since moving the decimal point changes the value, you have to multiply the decimal by a power of 10 so that the expression has the same value.
Let’s look at an example.
180,000. = 18,000.0 x 101
1,800.00 x 102
180.000 x 103
18.0000 x 104
1.80000 x 105
180,000 = 1.8 x 105
Notice that the decimal point was moved 5 places to the left, and the exponent is 5.
| The world population is estimated to be about 6,800,000,000 people. Which answer expresses this number in scientific notation?
A) 7 x 109
B) 0.68 x 1010
C) 6.8 x 109
D) 68 x 108
|
| Advanced Question Represent 1.00357 x 10-6 in decimal form.
A) 1.00357000000 B) 0.000100357 C) 0.000001357 D) 0.00000100357
|
To write a small number (between 0 and 1) in scientific notation, you move the decimal to the right and the exponent will have to be negative.
0.00004 = 00.0004 x 10-1
000.004 x 10-2
0000.04 x 10-3
00000.4 x 10-4
000004. x 10-5
0.00004 = 4 x 10-5
You may notice that the decimal point was moved five places to the right until you got the number 4, which is between 1 and 10. The exponent is −5.
You can also write scientific notation as decimal notation. For example, the number of miles that light travels in a year is 5.88 x 1012, and a hydrogen atom has a diameter of 5 x 10-8 mm. To write each of these numbers in decimal notation, you move the decimal point the same number of places as the exponent. If the exponent is positive, move the decimal point to the right. If the exponent is negative, move the decimal point to the left.
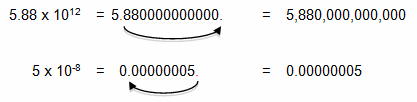
For each power of 10, you move the decimal point one place. Be careful here and don’t get carried away with the zeros—the number of zeros after the decimal point will always be 1 less than the exponent because it takes one power of 10 to shift that first number to the left of the decimal.
| Rewrite 1.57 x 10-10 in decimal notation.
A) 15,700,000,000
B) 0.000000000157
C) 0.0000000000157
D) 157 x 10-12
|
Numbers that are written in scientific notation can be multiplied and divided rather simply by taking advantage of the properties of numbers and the rules of exponents that you may recall. To multiply numbers in scientific notation, first multiply the numbers that aren’t powers of 10 (the a in a x 10n). Then multiply the powers of ten by adding the exponents.
This will produce a new number times a different power of 10. All you have to do is check to make sure this new value is in scientific notation. If it isn’t, you convert it.
Let’s look at some examples.
| Example | ||
| Problem | (3 x 108)(6.8 x 10-13) |
|
|
|
(3 x 6.8)(108 x 10-13) | Regroup, using the commutative and associative properties. |
|
|
(20.4)(108 x 10-13)
|
Multiply the coefficients. |
|
| 20.4 x 10-5 | Multiply the powers of 10, using the Product Rule—add the exponents. |
|
| (2.04 x 101) x 10-5 | Convert 20.4 into scientific notation by moving the decimal point one place to the left and multiplying by 101. |
|
| 2.04 x (101 x 10-5) | Group the powers of 10 using the associative property of multiplication. |
|
| 2.04 x 101+(-5) | Multiply using the Product Rule— add the exponents. |
| Answer | (3 x 108)(6.8 x 10-13) = 2.04 x 10-4 | |
| Advanced Example | ||
| Problem | (8.2 x 106)(1.5 x 10-3)(1.9 x 10-7) |
|
|
(8.2 x 1.5 x 1.9)(106 x 10-3 x 10-7) | Regroup, using the commutative and associative properties. | |
|
(23.37) (106 x 10-3 x 10-7)
|
Multiply the numbers. | |
|
| 23.37 x 10-4 | Multiply the powers of 10, using the Product Rule—add the exponents. |
|
| (2.337 x 101) x 10-4 | Convert 23.37 into scientific notation by moving the decimal point one place to the left and multiplying by 101. |
|
| 2.337 x (101 x 10-4) | Group the powers of 10 using the associative property of multiplication. |
|
| 2.337 x 101+(-4) | Multiply using the Product Rule and add the exponents. |
| Answer | (8.2 x 106)(1.5 x 10-3)(1.9 x 10-7) = 2.337 x 10-3 | |
In order to divide numbers in scientific notation, you once again apply the properties of numbers and the rules of exponents. You begin by dividing the numbers that aren’t powers of 10 (the a in a x 10n). Then you divide the powers of ten by subtracting the exponents.
This will produce a new number times a different power of 10. If it isn’t already in scientific notation, you convert it, and then you’re done.
Let’s look at some examples.
| Example | |||
| Problem |
|
| |
|
|
| Regroup, using the associative property. | |
|
| (0.82) |
Divide the coefficients. | |
|
| 0.82 x 10-9 – (-3)
0.82 x 10-6 | Divide the powers of 10 using the Quotient Rule—subtract the exponents. | |
|
| (8.2 ´ 10-1) x 10-6 | Convert 0.82 into scientific notation by moving the decimal point one place to the right and multiplying by 10-1. | |
|
| 8.2 ´ (10-1 x 10-6) | Group the powers of 10 together using the associative property. | |
|
| 8.2 x 10-1+(-6) | Multiply the powers of 10, using the Product Rule—add the exponents. | |
| Answer |
|
| |
| Advanced Example | |||
| Problem |
|
| |
|
| Regroup the terms in the numerator according to the associative and commutative properties. | ||
|
| Multiply. | ||
|
| Regroup, using the associative property. | ||
|
|
Divide the numbers. | ||
|
| Divide the powers of 10 using the Quotient Rule—subtract the exponents. | ||
| Answer |
| ||
Notice that when you divide exponential terms, you subtract the exponent in the denominator from the exponent in the numerator.
| Evaluate (4 x 10-10)(3 x 105) and express the result in scientific notation.
A) 1.2 x 10-4
B) 12 x 10-5
C) 7 x 10-5
D) 1.2 x 10-50
|
| Advanced Question Evaluate (3.15 x 104)(5.15 x 10-7) and express the result as a decimal.
A) 0.0162225 B) 162225 C) 0.000162225 D) 16.2225
|
Summary
Scientific notation was developed to assist mathematicians, scientists, and others when expressing and working with very large and very small numbers. Scientific notation follows a very specific format in which a number is expressed as the product of a number greater than or equal to one and less than ten, and a power of 10. The format is written a x 10n, where 1 ≤ a < 10 and n is an integer.
To multiply or divide numbers in scientific notation, you can use the commutative and associative properties to group the exponential terms together and apply the rules of exponents.