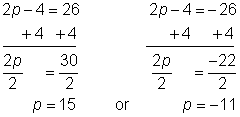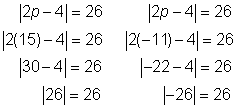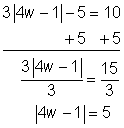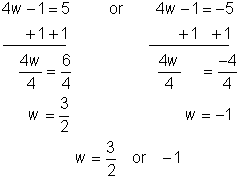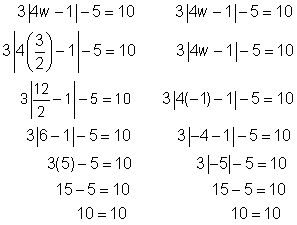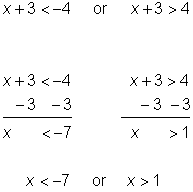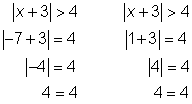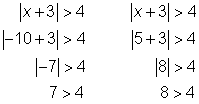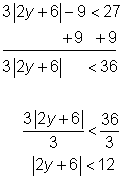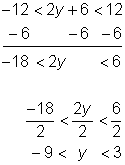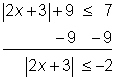Equations and Inequalities and Absolute Value

 

Learning Objective(s)

·         Solve equations containing absolute values.

·         Solve inequalities containing absolute values.

·         Identify cases of equations and inequalities containing absolute values which have no solutions.

 

The [absolute value] of a number or expression describes its distance from 0 on a number line. Since the absolute value expresses only the distance, not the direction of the number on a number line, it is always expressed as a positive number or 0.

 

For example, −4 and 4 both have an absolute value of 4 because they are each 4 units from 0 on a number line—though they are located in opposite directions from 0 on the number line.

 

When solving absolute value equations and inequalities, you have to consider both the behavior of absolute value and the properties of equality and inequality.

 

Because both positive and negative values have a positive absolute value, solving absolute value equations means finding the solution for both the positive and the negative values.

 

Let’s first look at a very basic example.

 

This equation is read “the absolute value of x is equal to five.” The solution is the value(s) that are five units away from 0 on a number line.

 

You might think of 5 right away; that is one solution to the equation. Notice that −5 is also a solution because −5 is 5 units away from 0 in the opposite direction. So, the solution to this equation  is x = −5 or x = 5.

 

A more complex absolute value problem is solved in a similar fashion. Consider . This equation asks you to find what number plus 5 has an absolute value of 15. Since 15 and −15 both have an absolute value of 15, the absolute value equation is true when the quantity x + 5 is 15 or x + 5 is −15, since |15| = 15 and |−15| = 15. So, you need to find out what value for x will make this expression equal to 15 as well as what value for x will make the expression equal to −15. Solving the two equations you get:

 

 

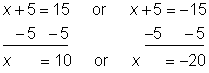
You can check these two solutions in the absolute value equation to see if x = 10 and x = −20 are correct.

 

 

 

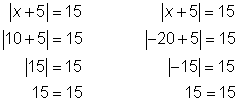
Solving Equations of the Form |x| = a   For any positive number a, the solution of |x| = a is                                                                           x = a  or  x = −a   x can be a single variable or any algebraic expression.

 

Let’s look at another example.

 

 

 

 

Sometimes, you have to isolate an absolute value before solving the equation. An example is shown below.

 

 

 

 

Let’s take a look at one more example:

Solve for y.

Before removing the absolute value sign and making two equations, think about what this equation means. It reads “the absolute value of the quantity 3y minus 5 is equal to −1.” Remember that an absolute value is the distance from 0 on a number line, so it must be a positive number. Since it’s impossible to have an absolute value equal to −1, this equation has no solution. There are no values for y that will make this a true statement. There is no additional work needed to know this equation has no solutions.

 

 

Let’s apply what you know about solving equations that contain absolute values and what you know about inequalities to solve inequalities that contain absolute values. Let’s start with a simple inequality.

 

 

This inequality is read, “the absolute value of x is less than or equal to 4.” If you are asked to solve for x, you want to find out what values of x are 4 units or less away from 0 on a number line. You could start by thinking about the number line and what values of x would satisfy this equation.

 

4 and −4 are both four units away from 0, so they are solutions. 3 and −3 are also solutions because each of these values is less than 4 units away from 0. So are 1 and −1, 0.5 and −0.5, and so on—there are an infinite number of values for x that will satisfy this inequality.

 

The graph of this inequality will have two closed circles, at 4 and −4. The distance between these two values on the number line is colored in blue because all of these values satisfy the equation.

 

 

The solution can be written this way:  −4  x  4.

 

The situation is a little different when the inequality sign is “greater than” or “greater than or equal to.”  Consider the simple inequality Again, you could think of the number line and what values of x are greater than 3 units away from zero. This time, 3 and −3 are not included in the solution, so there are open circles on both of these values. 2 and −2 would not be solutions because they are not more than 3 units away from 0. But, 5 and −5 would work and so would all of the values extending to the left of −3 and to the right of 3. The graph would look like the one below.

 

 

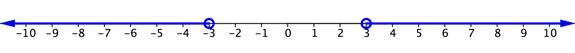
The solution to this inequality can be written this way: x < −3 or x > 3.

 

Solving Absolute Value Inequalities   For any positive value of a:   is equivalent to   (this rule also applies for )  is equivalent to x −a or xa (this rule also applies for )   x can be a single variable or any algebraic expression.

 

 

Solve the inequality:   A) p ≤ −5 or p ≥ 5 B) −5 ≤ p ≤ 5 C) p ≤ −5 D) No solution   Show/Hide Answer A) p ≤ −5 or p ≥ 5 Incorrect. This is the solution to |p| ≥ 5. For example, 7, which is greater than 5, is not a solution to the original inequality because |7| is 7, which is not less than 5. The correct answer is −5 ≤ p ≤ 5.   B) −5 ≤ p ≤ 5 Correct. The values of p that are greater than or equal to −5 and less than or equal to 5 satisfy this inequality.   C) p ≤ −5 Incorrect. If you substitute a value less than −5 into the original inequality, you get an untrue statement. For example, if p = −10, a value less than −5, then |−10| ≤ 5. This is not true because the absolute value of −10 is 10 and 10 is not less than or equal to 5. The correct answer is −5 ≤ p ≤ 5.   D) No solution Incorrect. The values greater than or equal to −5 and less than or equal to 5 satisfy the inequality. The correct answer is −5 ≤ p ≤ 5.

 

 

Let’s look at a few more examples of inequalities containing absolute values.

 

 

 

 

 

 

As with equations, there may be instances in which there is no solution to an inequality.

 

 

 

 

To solve an equation containing an absolute value, you want to isolate the absolute value expression. Once that is done, you can rewrite the absolute value equation as two equations, where one of the statements equates the value within the absolute value to the positive quantity on the other side of the equation and one that equates the value with the absolute value to the negative (or opposite) value.

 

Inequalities can also contain absolute values. Absolute inequalities also can be solved by rewriting them using compound inequalities.