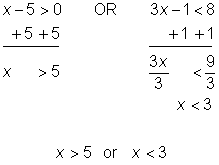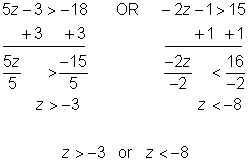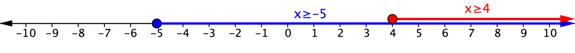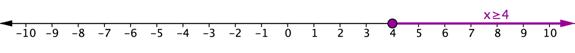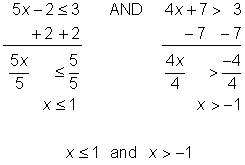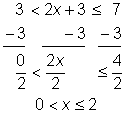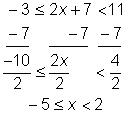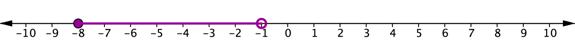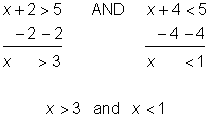Compound Inequalities

 

Learning Objectives

·         Solve compound inequalities in the form of or and express the solution graphically.

·         Solve compound inequalities in the form of and and express the solution graphically.

·         Solve compound inequalities in the form a < x < b.

·         Identify cases with no solution.

 

Many times, solutions lie between two quantities, rather than continuing endlessly in one direction. For example systolic (top number) blood pressure that is between 120 and 139 mm Hg is called borderline high blood pressure. This can be described using a compound inequality, b < 139 and b > 120. Other compound inequalities are joined by the word “or”.

 

When two inequalities are joined by the word and, the solution of the compound inequality occurs when both inequalities are true at the same time. It is the overlap, or intersection, of the solutions for each inequality. When the two inequalities are joined by the word or, the solution of the compound inequality occurs when either of the inequalities is true. The solution is the combination, or union, of the two individual solutions.

 

 

Let’s take a closer look at a compound inequality that uses or to combine two inequalities. For example, x > 6 or x < 2. The solution to this compound inequality is all the values of x in which x is either greater than 6 or x is less than 2. You can show this graphically by putting the graphs of each inequality together on the same number line.

 

 

The graph has an open circle on 6 and a blue arrow to the right and another open circle at 2 and a red arrow to the left. In fact, the only parts that are not a solution to this compound inequality are the points 2 and 6 and all the points in between these values on the number line. Everything else on the graph is a solution to this compound inequality.

 

Let’s look at another example of an or compound inequality, x > 3 or x ≤ 4. The graph of x > 3 has an open circle on 3 and a blue arrow drawn to the right to contain all the numbers greater than 3.

 

 

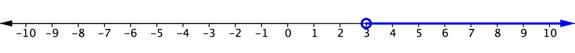
The graph of x ≤ 4 has a closed circle at 4 and a red arrow to the left to contain all the numbers less than 4.

 

 

What do you notice about the graph that combines these two inequalities?

 

 

Since this compound inequality is an or statement, it includes all of the numbers in each of the solutions, which in this case is all the numbers on the number line. (The region of the line greater than 3 and less than or equal to 4 is shown in purple because it lies on both of the original graphs.) The solution to the compound inequality x > 3 or x ≤ 4 is the set of all real numbers!

 

You may need to solve one or more of the inequalities before determining the solution to the compound inequality, as in the example below.

 

 

 

 

The solution to this compound inequality can be shown graphically.

 

 

Remember to apply the properties of inequality when you are solving compound inequalities. The next example involves dividing by a negative to isolate a variable.

 

 

 

 

This number line shows the solution set of y < 3 or y ≥ 4.

 

 

 

 

 

This number line shows the solution set of z > −3 or z < −8.

 

 

 

Solve for h. h + 3  > 12 or  3 – 2h > 9   A) h < 3 or h > −3 B) h > 9 or h > −3 C) h > −9 or h < 3 D) h > 9 or h < −3   Show/Hide Answer A) h < 3 or h > −3 Incorrect. To solve the inequality h + 3  > 12, subtract 3 from both sides to get h > 9. When you divide both sides of an inequality by a negative number, reverse the inequality sign to get h < −3 for the solution to the second inequality. The correct answer is h > 9 or h < −3.   B) h > 9 or h > −3 Incorrect. To solve the inequality 3 – 2h > 9, subtract 3 from both sides and then divide by −2. When you divide both sides of an inequality by a negative number, reverse the inequality sign to get h < −3. The correct answer is h > 9 or h < −3.   C) h > −9 or h < 3 Incorrect. Check a few values for h that are greater than −9 but less than 3, and see if they make the inequality true. For example, if you substitute h = 2 into each inequality, you get false statements:  2 + 3 > 9; 3 – 2(2) > 9. The correct answer is h > 9 or h < −3.   D) h > 9 or h < −3 Correct. Solving each inequality for h, you find that h > 9 or h < −3.

 

 

 

The solution of a compound inequality that consists of two inequalities joined with the word and is the intersection of the solutions of each inequality. In other words, both statements must be true at the same time. The solution to an and compound inequality are all the solutions that the two inequalities have in common. Graphically, you can think about it as where the two graphs overlap.

 

Think about the example of the compound inequality: x < 5 and x ≥ −1. The graph of each individual inequality is shown in color.

 

 

Since the word and joins the two inequalities, the solution is the overlap of the two solutions. This is where both of these statements are true at the same time.

 

 The solution to this compound inequality is shown below.

 

 

Notice that in this case, you can rewrite x ≥ −1 and x < 5 as −1 ≤ x < 5 since the solution is between −1 and 5, including −1. You read −1 ≤ x < 5 as “x is greater than or equal to −1 and less than 5.” You can rewrite an and statement this way only if the answer is between two numbers.

 

Let’s look at two more examples.

 

 

 

 

 

 

Rather than splitting a compound inequality in the form of a < x < b into two inequalities x < b and x > a, you can more quickly solve the inequality by applying the properties of inequality to all three segments of the compound inequality. Two examples are provided below.

 

 

 

 

 

 

To solve inequalities like a < x < b, use the addition and multiplication properties of inequality to solve the inequality for x. Whatever operation you perform on the middle portion of the inequality, you must also perform to each of the outside sections as well. Pay particular attention to division or multiplication by a negative.

 

 

Which of the following compound inequalities represents the graph on the number line below?     A) −8 ≥ x > −1 B) −8 ≤ x < −1 C) −8 ≤ x > −1 D) −8 ≥ x < −1   Show/Hide Answer A) −8 ≥ x > −1 Incorrect. This compound inequality reads, “x is less than or equal to −8 and greater than −1.” The shaded part of the graph includes values that are greater than or equal to −8 and less than −1. The correct answer is −8 ≤ x < −1.   B) −8 ≤ x < −1 Correct. The selected region on the number line lies between −8 and −1and includes -8, so x must be greater than or equal to −8 and less than −1.   C) −8 ≤ x > −1 Incorrect. This compound inequality reads, “x is greater than or equal to −8 and greater than −1.” The values that are shaded are less −1, not greater. The correct answer is −8 ≤ x < −1.   D) −8 ≥ x < −1 Incorrect. This compound inequality reads, “x is less than or equal to −8 and less than −1.” The graph does not include values that are less than or equal to −8. It includes values that are greater than or equal to −8 and less than −1. The correct answer is −8 ≤ x < −1.

 

 

The solution to a compound inequality with and is always the overlap between the solution to each inequality. There are three possible outcomes for compound inequalities joined by the word and:

1. The solution could be all the values between two endpoints.

 

 

2. The solution could begin at a point on the number line and extend in one direction.

 

 

 

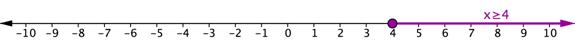
3. In cases where there is no overlap between the two inequalities, there is no solution to the compound inequality.

 

 

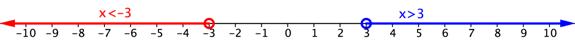
An example is shown below.

 

 

 

 

A compound inequality is a statement of two inequality statements linked together either by the word or or by the word and. Sometimes, an and compound inequality is shown symbolically, like a < x < b, and does not even need the word and. Because compound inequalities represent either a union or intersection of the individual inequalities, graphing them on a number line can be a helpful way to see or check a solution. Compound inequalities can be manipulated and solved much the same way any inequality is solved, paying attention to the properties of inequalities and the rules for solving them.