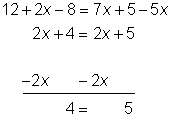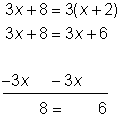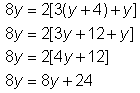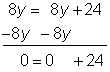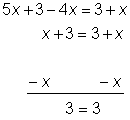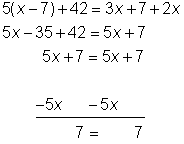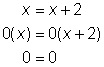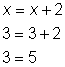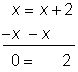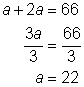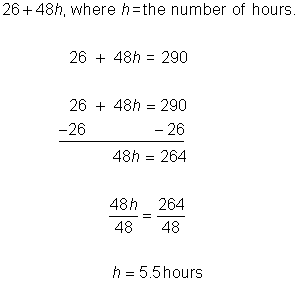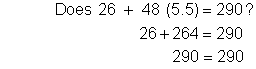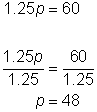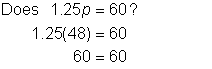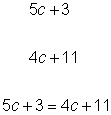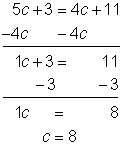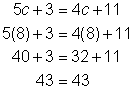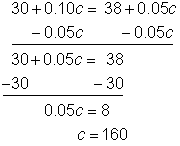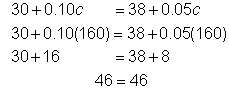Special Cases and Applications
Learning Objective(s)
· Solve equations that have one solution, no solution, or an infinite number of solutions.
· Solve application problems by using an equation in one variable.
Introduction
When you follow the steps to solve an equation, you try to isolate the variable. You have a solution when you get the equation x = some value. There are equations, however, that have no solution, and other equations that have an infinite number of solutions. How does this work?
Let’s apply the steps for solving an algebraic equation to the equation below.
Example | ||
| Problem | Solve for x. 12 + 2x – 8 = 7x + 5 – 5x | |
|
|
| Combine like terms on both sides of the equation.
Isolate the x term by subtracting 2x from both sides. |
This is not a solution! You did not find a value for x. Solving for x the way you know how, you arrive at the false statement 4 = 5. Surely 4 cannot be equal to 5!
This may make sense when you consider the second line in the solution where like terms were combined. If you multiply a number by 2 and add 4 you would never get the same answer as when you multiply that same number by 2 and add 5. Since there is no value of x that will ever make this a true statement, the solution to the equation above is “no solution”.
Be careful that you do not confuse the solution x = 0 with “no solution”. The solution x = 0 means that the value 0 satisfies the equation, so there is a solution. “No solution” means that there is no value, not even 0, which would satisfy the equation.
Also, be careful not to make the mistake of thinking that the equation 4 = 5 means that 4 and 5 are values for x that are solutions. If you substitute these values into the original equation, you’ll see that they do not satisfy the equation. This is because there is truly no solution—there are no values for x that will make the equation 12 + 2x – 8 = 7x + 5 – 5x true.
| Example | |||
| Problem | Solve for x. 3x + 8 = 3(x + 2) | ||
|
|
| Apply the distributive property to simplify.
Isolate the variable term. Since you know that 8 = 6 is false, there is no solution.
| |
| Answer | There is no solution. |
| |
| Advanced Example | ||
| Problem | Solve for y. 8y = 2[3(y + 4) + y] | |
|
| Apply the distributive property to simplify. When two sets of grouping symbols are used, evaluate the inner set and then evaluate the outer set. | |
|
| | Isolate the variable term by subtracting 8y from both sides of the equation. Since you know that 0 = 24 is false, there is no solution. |
| Answer | There is no solution. |
|
Algebraic Equations with an Infinite Number of Solutions
You have seen that if an equation has no solution, you end up with a false statement instead of a value for x. You can probably guess that there might be a way you could end up with a true statement instead of a value for x.
| Example | ||
| Problem | Solve for x. 5x + 3 – 4x = 3 + x | |
|
|
| Combine like terms on both sides of the equation.
Isolate the x term by subtracting x from both sides. |
You arrive at the true statement “3 = 3”. When you end up with a true statement like this, it means that the solution to the equation is “all real numbers”. Try substituting x = 0 into the original equation—you will get a true statement! Try ![]() , and it also will check!
, and it also will check!
This equation happens to have an infinite number of solutions. Any value for x that you can think of will make this equation true. When you think about the context of the problem, this makes sense—the equation x + 3 = 3 + x means “some number plus 3 is equal to 3 plus that same number.” We know that this is always true—it’s the commutative property of addition!
| Example | ||
| Problem | Solve for x. 5(x – 7) + 42 = 3x + 7 + 2x | |
|
| Apply the distributive property and combine like terms to simplify.
Isolate the x term by subtracting 5x from both sides. You get the true statement 7 = 7, so you know that x can be all real numbers. | |
| Answer | x = all real numbers |
|
When solving an equation, multiplying both sides of the equation by zero is not a good choice. Multiplying both side of an equation by 0 will always result in an equation of 0 = 0, but an equation of 0 = 0 does not help you know what the solution to the original equation is.
| Example | |||
| Problem | Solve for x. x = x + 2 | ||
|
| Multiply both sides by zero.
While it is true that 0 = 0, and you may be tempted to conclude that x is true of all real numbers, that is not the case. | ||
|
Check:
Better Method:
|
For example, check and see if x = 3 will solve the equation.
Clearly 3 never equals 5, so x = 3 is not a solution. The equation has no solutions.
It was not helpful to have multiplied both sides of the equation by zero.
It would have been better to have started by subtracting x from both sides, resulting in 0 = 2, resulting in a false statement telling us that there are no solutions. | ||
| Answer | There is no solution. |
| |
| In solving the algebraic equation 2(x – 5) = 2x + 10, you end up with −10 = 10. What does this mean?
A) x = −10 and 10 B) There is no solution to the equation. C) You must have made a mistake in solving the equation. D) x = all real numbers
|
| Advanced Question How many solutions are there for the equation:
A) There is one solution. B) There are two solutions. C) There are an infinite number of solutions. D) There are no solutions.
|
The power of algebra is how it can help you model real situations in order to answer questions about them. This requires you to be able to translate real-world problems into the language of algebra, and then be able to interpret the results correctly. Let’s start by exploring a simple word problem that uses algebra for its solution.
Amanda’s dad is twice as old as she is today. The sum of their ages is 66. Use an algebraic equation to find the ages of Amanda and her dad.
One way to solve this problem is to use trial and error—you can pick some numbers for Amanda’s age, calculate her father’s age (which is twice Amanda’s age), and then combine them to see if they work in the equation. For example, if Amanda is 20, then her father would be 40 because he is twice as old as she is, but then their combined age is 60, not 66. What if she is 12? 15? 20? As you can see, picking random numbers is a very inefficient strategy!
You can represent this situation algebraically, which provides another way to find the answer.
| Example | ||||||
| Problem |
| Amanda’s dad is twice as old as she is today. The sum of their ages is 66. Find the ages of Amanda and her dad. | ||||
|
| We need to find Amanda’s age and her father’s age. |
| What is the problem asking? | |||
|
|
| Assign a variable to the unknown. The father’s age is two times Amanda’s age. | ||||
|
|
| Amanda’s age added to her father’s age is equal to 66. | ||||
|
|
| Solve the equation for the variable. | ||||
|
|
| Use Amanda’s age to find her father’s age. | ||||
|
|
| Do the answers make sense? | ||||
| Answer |
| Amanda is 22 years old, and her father is 44 years old. | ||||
Let’s try a new problem. Consider that the rental fee for a landscaping machine includes a one-time fee plus an hourly fee. You could use algebra to create an expression that helps you determine the total cost for a variety of rental situations. An equation containing this expression would be useful for trying to stay within a fixed expense budget.
| Example | ||
| Problem | A landscaper wants to rent a tree stump grinder to prepare an area for a garden. The rental company charges a $26 one-time rental fee plus $48 for each hour the machine is rented.
Write an expression for the rental cost for any number of hours. | |
|
| The problem asks for an algebraic expression for the rental cost of the stump grinder for any number of hours. An expression will have terms, one of which will contain a variable, but it will not contain an equal sign. | What is the problem asking? |
|
| Look at the values in the problem:
$26 = one-time fee $48 = per-hour fee
Think about what this means, and try to identify a pattern.
1 hr rental: $26 + $48 2 hr rental: $26 + $48 + $48 3 hr rental: $26 + $48 + $48 + $48
Notice that the number of “+ $48” in the problem is the same as the number of hours the machine is being rented. Since multiplication is repeated addition, you could also represent it like this:
1 hr rental: $26 + $48(1) 2 hr rental: $26 + $48(2) 3 hr rental: $26 + $48(3)
| What information is important to finding an answer?
|
|
| Now let’s use a variable, h, to represent the number of hours the machine is rented.
Rental for h hours: 26 + 48h
| What is the variable?
What expression models this situation?
The total rental fee is determined by multiplying the number of hours by $48 and adding $26. |
| Answer | The rental cost for h hours is 26 + 48h. | |
Using the information provided in the problem, you were able to create a general expression for this relationship. This means that you can find the rental cost of the machine for any number of hours!
Let’s use this new expression to solve another problem.
| Example | ||
| Problem | A landscaper wants to rent a tree stump grinder to prepare an area for a garden. The rental company charges a $26 one-time rental fee plus $48 for each hour the machine is rented.
What is the maximum number of hours the landscaper can rent the tree stump grinder, if he can spend no more than $290? (The machine cannot be rented for part of an hour.) | |
| 26 + 48h, where h = the number of hours. | What expression models this situation? | |
|
| Write an equation to help you find out when the expense equals $290.
Solve the equation. | |
|
| Check the solution. | |
|
| Interpret the answer. | |
| Answer | The landscaper can rent the machine for 5 hours. | |
It is often helpful to follow a list of steps to organize and solve application problems.
| Solving Application Problems
Follow these steps to translate problem situations into algebraic equations you can solve.
1. Read and understand the problem. 2. Determine the constants and variables in the problem. 3. Write an equation to represent the problem. 4. Solve the equation. 5. Check your answer. 6. Write a sentence that answers the question in the application problem.
|
Let’s try applying the problem-solving steps with some new examples.
| Example | |||
| Problem | Gina has found a great price on paper towels. She wants to stock up on these for her cleaning business. Paper towels cost $1.25 per package. If she has $60 to spend, how many packages of paper towels can she purchase? Write an equation that Gina could use to solve this problem and show the solution. | ||
|
| The problem asks for how many packages of paper towels Gina can purchase. | What is the problem asking you? | |
|
| The paper towels cost $1.25 per package. Gina has $60 to spend on paper towels. | What are the constants?
| |
|
| Let p = the number of packages of paper towels. | What is the variable? | |
|
| What equation represents this situation?
Solve for p. Divide both sides of the equation by 1.25
60 ÷ 1.25 = 6,000 ÷ 125
5 00 1,000 1,000 0
| ||
|
|
| Check your solution. Substitute 48 in for p in your equation. | |
| Answer | Gina can purchase 48 packages of paper towels. | ||
| Example | ||
| Problem | Levon and Maria were shopping for candles to decorate tables at a restaurant. Levon bought 5 packages of candles plus 3 single candles. Maria bought 11 single candles plus 4 packages of candles. Each package of candles contains the same number of candles. After finishing shopping, Maria and Levon realized that they had each purchased the same exact number of candles. How many candles are in a package? | |
| The problem asks how many candles are contained in one package. | What is the problem asking you? | |
| Levon bought 5 packages and 3 single candles.
Maria bought 4 packages and 11 single candles. | What are the constants?
| |
| Let c = the number of candles in one package. | What is the variable? | |
|
|
| What expression represents the number of candles Levon purchased? What expression represents the number of candles Maria purchased? What equation represents the situation? |
|
| Maria and Levon bought the same number of candles. | |
|
|
| Solve for c. Subtract 4c from both sides.
Subtract 3 from both sides. |
|
|
| Check your solution. Substitute 8 for c in the original equation. |
| Answer | There are 8 candles in one package of candles. | |
| Advanced Example | ||
| Problem | The money from two vending machines is being collected. One machine contains 30 dollar bills and a bunch of dimes. The other machine contains 38 dollar bills and a bunch of nickels. The number of coins in both machines is equal, and the amount of money that the machines collected is also equal. How many coins are in each machine? | |
|
| The problem asks how many coins are in each machine. | What is the problem asking you? |
|
| One machine has 30 dollar bills and a bunch of dimes.
Another machine has 38 dollar bills and a bunch of nickels—the same number of coins as the first machine. | What are the constants and what are the unknowns?
|
|
| Let c = the number of coins in each machine. | What is the variable? |
|
|
| What expression represents the amount of money in the first machine? |
|
|
| What expression represents the amount of money in the second machine? |
|
|
| What equation represents the situation? The amount of money in both machines is the same. |
|
|
| Solve for c. |
|
|
| Check your solution. Substitute 160 for c in the original equation. |
| Answer | There are 160 coins in each machine. | |
| Advanced Question Albert and Bryn are buying candy at the corner store. Albert buys 5 bags and 3 individual pieces; Bryn buys 3 bags and then eats 2 pieces of candy from one of the bags. Each bag has the same number of pieces of candy.
After Bryn eats the 2 pieces, she has exactly half the number of pieces of candy as Albert. How many pieces of candy are in each bag?
Pick the equation that could be used to solve the problem above. Use the variable b to represent the number of pieces of candy in one bag.
A) B) C) D)
|
Summary
Some equations are considered special cases. These are equations that have no solution and equations whose solution is the set of all real numbers. When you use the steps for solving an equation, and you get a false statement rather than a value for the variable, there is no solution. When you use the steps for solving an equation, have avoided multiplying both sides of the equation by zero, and you get a true statement rather than a value for the variable, the solution is all real numbers. Algebra is a powerful tool for modeling and solving real-world problems.