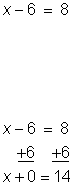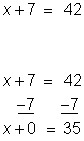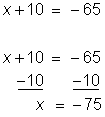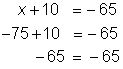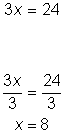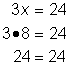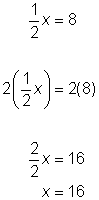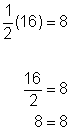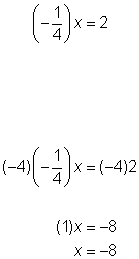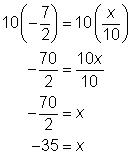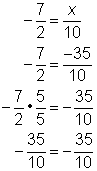Solving One-Step Equations Using Properties of Equality
Learning Objective(s)
· Solve algebraic equations using the addition property of equality.
· Solve algebraic equations using the multiplication property of equality.
Introduction
Writing and solving equations is an important part of mathematics. Algebraic equations can help you model situations and solve problems in which quantities are unknown. The simplest type of algebraic equation is a linear equation that has just one variable.
Expressions and Equations
An equation is a mathematical statement that two expressions are equal. An equation will always contain an equal sign with an expression on each side. Expressions are made up of terms, and the number of terms in each expression in an equation may vary.
Algebraic equations contain variables, symbols that stand for an unknown quantity. Variables are often represented with letters, like x, y, or z. Sometimes a variable is multiplied by a number. This number is called the coefficient of the variable. For example, the coefficient of 3x is 3.
An important property of equations is one that states that you can add the same quantity to both sides of an equation and still maintain an equivalent equation. Sometimes people refer to this as keeping the equation “balanced”. If you think of an equation as being like a balance scale, the quantities on each side of the equation are equal, or balanced.
Let’s look at a simple numeric equation, 3 + 7 =10, to explore the idea of an equation as being balanced.

The expressions on each side of the equal sign are equal, so you can add the same value to each side and maintain the equality. Let’s see what happens when 5 is added to each side.
3 + 7 + 5 = 10 + 5
Since each expression is equal to 15, you can see that adding 5 to each side of the original equation resulted in a true equation. The equation is still “balanced.”
On the other hand, let’s look at what would happen if you added 5 to only one side of the equation.
3 + 7 = 10
3 + 7 + 5 = 10
15 ≠ 10
Adding 5 to only one side of the equation resulted in an equation that is false. The equation is no longer “balanced”, and it is no longer a true equation!
|
Addition Property of Equality
For all real numbers a, b, and c: If a = b, then a + c = b + c.
If two expressions are equal to each other, and you add the same value to both sides of the equation, the equation will remain equal.
|
When you solve an equation, you find the value of the variable that makes the equation true. In order to solve the equation, you isolate the variable. Isolating the variable means rewriting an equivalent equation in which the variable is on one side of the equation and everything else is on the other side of the equation.
When the equation involves addition or subtraction, use the inverse operation to “undo” the operation in order to isolate the variable. For addition and subtraction, your goal is to change any value being added or subtracted to 0, the additive identity.
| Example | ||
| Problem | Solve x – 6 = 8. |
|
|
| This equation means that if you begin with some unknown number, x, and subtract 6, you will end up with 8. You are trying to figure out the value of the variable x.
Using the Addition Property of Equality, add 6 to both sides of the equation to isolate the variable. You choose to add 6, as 6 is being subtracted from the variable. | |
| Answer | x = 14 |
|
Since subtraction can be written as addition (adding the opposite), the addition property of equality can be used for subtraction as well. So just as you can add the same value to each side of an equation without changing the meaning of the equation, you can subtract the same value from each side of an equation.
| Example | ||
| Problem | Solve x + 7 = 42. |
|
|
| Since 7 is being added to the variable, subtract 7 to isolate the variable.
To keep the equation balanced, subtract 7 from both sides of the equation. | |
| Answer | x = 35 |
|
| Advanced Example | ||
| Problem | Solve 12.5 + x = -7.5. | |
|
| 12.5 + x = -7.5 | Since 12.5 is being added to the variable, subtract 12.5 to isolate the variable. |
|
| 12.5 + x = -7.5 – 12.5 −12.5 0 + x = - 20 | To keep the equation balanced, subtract 12.5 from both sides of the equation. |
| Answer | x = -20 |
|
The examples above are sometimes called one-step equations because they require only one step to solve. In these examples, you either added or subtracted a constant from both sides of the equation to isolate the variable and solve the equation.
| What would you do to isolate the variable in the equation below, using only one step? x + 10 = 65
A) Add 10 to both sides of the equation. B) Subtract 10 from the left side of the equation only. C) Add 65 to both sides of the equation. D) Subtract 10 from both sides of the equation.
|
| Advanced Question What would you do to isolate the variable in the equation below, using only one step?
A) Subtract B) Add C) Subtract D) Add
|
With any equation, you can check your solution by substituting the value for the variable in the original equation. In other words, you evaluate the original equation using your solution. If you get a true statement, then your solution is correct.
| Example | |||
| Problem | Solve x + 10 = –65. Check your solution. | ||
|
| Since 10 is being added to the variable, subtract 10 from both sides. Note that subtracting 10 is the same as adding –10. | ||
| Check: |
| To check, substitute the solution, –75 for x in the original equation. Simplify. This equation is true, so the solution is correct. | |
| Answer | x = –75 is the solution to the equation x + 10 = –65. | ||
It is always a good idea to check your answer whether it is requested or not.
Just as you can add or subtract the same exact quantity on both sides of an equation, you can also multiply both sides of an equation by the same quantity to write an equivalent equation. Let’s look at a numeric equation, 5 • 3 = 15, to start. If you multiply both sides of this equation by 2, you will still have a true equation.
5 • 3 = 15
5 • 3 • 2 = 15 • 2
30 = 30
This characteristic of equations is generalized in the multiplication property of equality.
|
Multiplication Property of Equality
For all real numbers a, b, and c: If a = b, then a • c = b • c (or ab = ac).
If two expressions are equal to each other and you multiply both sides by the same number, the resulting expressions will also be equivalent.
|
When the equation involves multiplication or division, you can “undo” these operations by using the inverse operation to isolate the variable. When the operation is multiplication or division, your goal is to change the coefficient to 1, the multiplicative identity.
| Example | ||||
| Problem | Solve 3x = 24. Check your solution. | |||
|
| Divide both sides of the equation by 3 to isolate the variable (have a coefficient of 1).
Dividing by 3 is the same as having multiplied by
| |||
| Check |
| Check by substituting your solution, 8, for the variable in the original equation. The solution is correct! | ||
| Answer |
|
| ||
You can also multiply the coefficient by the multiplicative inverse (reciprocal) in order to change the coefficient to 1.
| Example | ||
| Problem | Solve | |
|
| The coefficient of
Multiply. | |
| Check |
| Check by substituting your solution into the original equation.
The solution is correct! |
| Answer | x = 16 |
|
| Example | ||
| Problem | Solve | |
|
| The coefficient of the variable is
Multiply.
Any number multiplied by its multiplicative inverse is equal to 1, so x = −8. | |
| Check |
| Check by substituting your solution into the original equation.
The solution is correct. |
| Answer | x = −8 | |
| Advanced Example | ||
| Problem | Solve | |
|
| This problem contains two fractions. Multiply both sides by 10 in order to isolate the variable x. Then simplify the fractions. | |
| Check |
| Check your answer by substituting
The solution is correct. |
| Answer |
|
|
| Solve for x: 5x = −100
A) x = 20 B) x = −20 C) x = 500 D) x = −500
|
| Advanced Question Solve for y: 4.2 = 7y
A) y = 0.6 B) y = 29.4 C) y = 1.67 D) y = -2.8
|
Summary
Equations are mathematical statements that combine two expressions of equal value. An algebraic equation can be solved by isolating the variable on one side of the equation using the properties of equality. To check the solution of an algebraic equation, substitute the value of the variable into the original equation.