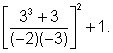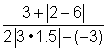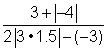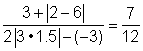Order of Operations

 

Learning Objective(s)

·         Use the order of operations to simplify expressions.

·         Simplify expressions containing absolute values.

 

Introduction

 

People need a common set of rules for performing basic calculations. What does 3 + 5 • 2 equal? Is it 16 or 13? Your answer depends on how you understand the order of operations — a set of rules that tell you the order in which addition, subtraction, multiplication, and division are performed in any calculation.

 

Mathematicians have developed a standard order of operations that tells you which calculations to make first in an expression with more than one operation. Without a standard procedure for making calculations, two people could get two different answers to the same problem.

 

The Four Basic Operations

 

The building blocks of the order of operations are the arithmetic operations: addition, subtraction, multiplication, and division. The order of operations states:

 

What is the correct answer for the expression 3 + 5 • 2? Use the order of operations listed above.

 

Multiply first.          3 + 5 • 2 = 3 + 10

Then add.              3 + 10 = 13

 

This order of operations is true for all real numbers.

 

Example

Problem

Simplify 7 – 5 + 3 · 8.

 

7 – 5 + 3 • 8

According to the order of operations, multiplication comes before addition and subtraction. Multiply 3 · 8.

 

7 – 5 + 24

Now, add and subtract from left to right. 7 – 5 comes first.

 

2 + 24 = 26

Finally, add 2 + 24.

Answer

7 – 5 + 3 • 8 = 26

 

 

When you are applying the order of operations to expressions that contain fractions, decimals, and negative numbers, you will need to recall how to do these computations as well.

 

Example

Problem

Simplify

 

According to the order of operations, multiplication comes before addition and subtraction. Multiply  first.

 

 

Now, divide .

 

1 – 32 = −31

Subtract.

Answer

 

 

 

Exponents

 

When you are evaluating expressions, you will sometimes see exponents used to represent repeated multiplication. Recall that an expression such as  is exponential notation for 7 • 7. (Exponential notation has two parts: the base and the exponent or the power. In , 7 is the base and 2 is the exponent; the exponent determines how many times the base is multiplied by itself.)

 

Exponents are a way to represent repeated multiplication; the order of operations places it before any other multiplication, division, subtraction, and addition is performed.

 

Example

Problem

Simplify .

 

This problem has exponents and multiplication in it. According to the order of operations, simplifying 32 and 23 comes before multiplication.

 

 is 3 · 3, which equals 9.

 

 is 2 · 2 · 2, which equals 8.

 

Multiply.

Answer

 

 

 

Example

Problem

Simplify .

 

This problem has exponents, multiplication, and addition in it. According to the order of operations, simplify the terms with the exponents first, then multiply, then add.

 

Evaluate:

 

Evaluate:

 

 

Multiply.

 

Simplify. , so you can add .

Answer

 

 

 

Simplify: .

 

A) −300

 

B) 0

 

C) 100

 

D) 300

 

Show/Hide Answer

A) −300

Incorrect. You may have found 4 · 5 = 20, squared 20, and then subtracted 400 from 100. The order of operations states that you should simplify the term with the exponent first, then multiply, then subtract.  = 25, and 25 · 4 = 100, and 100 – 100 = 0. The correct answer is 0.

 

B) 0

Correct. To simplify this expression, simplify the term with the exponent first, then multiply, then subtract.  = 25, and 25 · 4 = 100, and 100 – 100 = 0.

 

C) 100

Incorrect. The order of operations states that you should simplify the term with the exponent first, then multiply, then subtract.  = 25, and 25 · 4 = 100, and 100 – 100 = 0. The correct answer is 0.

 

D) 300

Incorrect. You may have found that  = 25, subtracted that from 100, and multiplied by 4. The order of operations states that you should simplify the term with the exponent first, then multiply, then subtract.  = 25, and 25 · 4 = 100, and 100 – 100 = 0. The correct answer is 0.

 

 

 

Grouping Symbols

 

The final piece that you need to consider in the order of operations is grouping symbols. These include parentheses ( ), brackets [ ], braces { }, and even fraction bars. These symbols are often used to help organize mathematical expressions (you will see them a lot in algebra).

 

Grouping symbols are used to clarify which operations to do first, especially if a specific order is desired. If there is an expression to be simplified within the grouping symbols, follow the order of operations.

 

The Order of Operations

 

·         Perform all operations within grouping symbols first. Grouping symbols include parentheses ( ), brackets [ ], braces { }, and fraction bars.

·         Evaluate exponents or square roots.

·         Multiply or divide, from left to right.

·         Add or subtract, from left to right.

 

 

When there are grouping symbols within grouping symbols, calculate from the inside to the outside. That is, begin simplifying within the innermost grouping symbols first.

 

Remember that parentheses can also be used to show multiplication. In the example that follows, both uses of parentheses—as a way to represent a group, as well as a way to express multiplication—are shown.

 

Example

Problem

Simplify (3 + 4)2 + (8)(4).

 

(3 + 4)2 + (8)(4)

 

 

 

 

 

 

(3 + 4)2 + (8)(4)

This problem has parentheses, exponents, multiplication, and addition in it. The first set of parentheses is a grouping symbol. The second set indicates multiplication.

 

Grouping symbols are handled first. Add numbers in parentheses.

 

72 + (8)(4)

49 + (8)(4)  

Simplify 72.

Perform multiplication.

 

49 + 32 = 81

Perform addition.

Answer

(3 + 4)2 + (8)(4) = 81

 

 

 

Example

Problem

Simplify (1.5 + 3.5) – 2(0.5 · 6)2.

 

(1.5 + 3.5) – 2(0.5 · 6)2

This problem has parentheses, exponents, multiplication, subtraction, and addition in it.

 

Grouping symbols are handled first. Add numbers in the first set of parentheses.

 

5 – 2(0.5 · 6)2

 

Multiply numbers in the second set of parentheses.

 

5 – 2(3)2

 

Evaluate exponents.

 

5 – 2 · 9

 

Multiply.

 

5 – 18 = −13

Subtract.

Answer

(1.5 + 3.5) – 2(0.5 · 6)2 = −13

 

 

 

Example

Problem

Simplify

 

This problem has brackets, parentheses, fractions, exponents, multiplication, subtraction, and addition in it.

 

Grouping symbols are handled first. The parentheses around the -6 aren’t a grouping symbol, they are simply making it clear that the negative sign belongs to the 6. Start with the innermost set of parentheses that are a grouping symbol , here it is in the numerator of the fraction, (2 · −6), and begin working out. (The fraction line acts as a type of grouping symbol, too; you simplify the numerator and denominator independently, and then divide the numerator by the denominator at the end.)

 

Add the values in the brackets.

 

Subtract 5 – [−9] = 5 + 9 = 14.

 

The top of the fraction is all set, but the bottom (denominator) has remained untouched. Apply the order of operations to that as well. Begin by evaluating 32 = 9.

 

 

Now add. 9 + 2 = 11.

 

 

Answer

 

 

 

Simplify

 

A) 25

 

B) 26

 

C) 151

 

D)

 

Show/Hide Answer

A) 25

Incorrect. You may have forgotten to add the 1! Simplify the expressions within the grouping symbols first (5), then square that expression (25), then add 1. The correct answer is 26.

 

B) 26

Correct. The entire quantity within the brackets is 5. 52 is 25, and 25 + 1 = 26.

 

C) 151

Incorrect. You may have squared the numerator of the fraction without simplifying the entire fraction first! Simplify the entire expression within the grouping symbols first (5), then square that expression (25), then add 1. The correct answer is 26.

 

D)

Incorrect. You may have squared the denominator of the fraction without simplifying the entire fraction first! Simplify the entire expression within the grouping symbols first (5), then square that expression (25), then add 1. The correct answer is 26.

 

 

 

Remembering the Order of Operations

 

The Order of Operations

 

·         Perform all operations within grouping symbols first. Grouping symbols include parentheses ( ), brackets [ ], braces { }, and fraction bars.

·         Evaluate exponents or square roots.

·         Multiply or divide, from left to right.

·         Add or subtract, from left to right.

 

 

The order of operations is important to know, but it is sometimes hard to remember. Some people use a saying to help them remember the order of operations. This saying is “Please Excuse My Dear Aunt Sally,” or “PEMDAS” for short. The first letter of each word begins with the same letter of an arithmetic operation.

 

Please  Parentheses (and other grouping symbols)

Excuse  Exponents (and roots)

My Dear  Multiplication and Division (from left to right)

Aunt Sally  Addition and Subtraction (from left to right)


Note: Even though multiplication comes before division in the saying, division could be performed first. Whether multiplication or division is performed first is determined by which comes first when reading from left to right. The same is true of addition and subtraction. Don’t let the saying confuse you about this!

 

Absolute Value Expressions

 

Absolute value expressions are one final method of grouping that you may see. Recall that the absolute value of a quantity is always positive or 0.

 

When you see an absolute value expression included within a larger expression, follow the regular order of operations and evaluate the expression within the absolute value sign. Then take the absolute value of that expression. The example below shows how this is done.

 

Example

Problem

Simplify

 

This problem has absolute values, decimals, multiplication, subtraction, and addition in it.

 

Grouping symbols, including absolute value, are handled first. Simplify the numerator, then the denominator. Evaluate |2 – 6|.

 

Take the absolute value of

|−4|.

 

Add the numbers in the numerator.

 

Now that the numerator is simplified, turn to the denominator. Evaluate the absolute value expression first.

 

 

The expression “2|4.5|” reads “2 times the absolute value of 4.5.” Multiply 2 times 4.5.

 

Subtract.

 

 

Answer

 

 

 

Simplify: (5|3 – 4|)3.

 

A) −125

 

B) 1331

 

C) −49

 

D) 125

 

Show/Hide Answer

A) −125

Incorrect. You may have forgotten to take the absolute value of the expression |3 – 4|. Remember that the absolute value will be either 0 or a positive number. |3 – 4| = |−1| = 1, and 5 times 1 is 5. The correct answer is 125.

 

B) 1331

Incorrect. You may have ignored the absolute value expression and found 113. Evaluate |3 – 4|, multiply that by 5, and then cube that number: |3 – 4| = |−1| = 1, and 5 times 1 is 5;

53 = 125. The correct answer is 125.

 

C) −49

Incorrect. You may have subtracted 43 from 5(3). Evaluate |3 – 4|, multiply that by 5, and then cube that number: |3 – 4| = |−1| = 1, and 5 times 1 is 5; 53 = 125. The correct answer is 125.

 

D) 125

Correct. |3 – 4| = |−1| = 1, and 5 times 1 is 5. 5 cubed is 125.

 

 

 

Summary

 

The order of operations gives us a standard, consistent method to use when simplifying strings of numbers and algebraic expressions. Without the order of operations, different people could come up with different answers to the same computation problem. Some people remember the order of operations by using the phrase “Please Excuse My Dear Aunt Sally” or, more simply, PEMDAS.