Associative, Commutative, and Distributive Properties

 

Learning Objective(s)

·         Identify and use the commutative properties for addition and multiplication.

·         Identify and use the associative properties for addition and multiplication.

·         Identify and use the distributive property.

 

 

There are many times in algebra when you need to simplify an expression. The properties of real numbers provide tools to help you take a complicated expression and simplify it.

 

The associative, commutative, and distributive properties of algebra are the properties most often used to simplify algebraic expressions. You will want to have a good understanding of these properties to make the problems in algebra easier to work.

 

 

You may encounter daily routines in which the order of tasks can be switched without changing the outcome. For example, think of pouring a cup of coffee in the morning. You would end up with the same tasty cup of coffee whether you added the ingredients in either of the following ways:

 

·         Pour 12 ounces of coffee into mug, then add splash of milk.

·         Add a splash of milk to mug, then add 12 ounces of coffee.

 

The order that you add ingredients does not matter. In the same way, it does not matter whether you put on your left shoe or right shoe first before heading out to work. As long as you are wearing both shoes when you leave your house, you are on the right track!

 

In mathematics, we say that these situations are commutative—the outcome will be the same (the coffee is prepared to your liking; you leave the house with both shoes on) no matter the order in which the tasks are done.

 

Likewise, the commutative property of addition states that when two numbers are being added, their order can be changed without affecting the sum. For example, 30 + 25 has the same sum as 25 + 30.

 

30 + 25 = 55

25 + 30 = 55

 

Multiplication behaves in a similar way. The commutative property of multiplication states that when two numbers are being multiplied, their order can be changed without affecting the product. For example, 7 · 12 has the same product as 12 · 7.

 

7 · 12 = 84

12 · 7 = 84

 

These properties apply to all real numbers. Let’s take a look at a few addition examples.

 

 

 

 

Commutative Property of Addition

For any real numbers a and b, a + b = b + a.

 

Subtraction is not commutative. For example, 4 − 7 does not have the same difference as 7 − 4. The − sign here means subtraction.

 

However, recall that 4 − 7 can be rewritten as 4 + (−7), since subtracting a number is the same as adding its opposite. Applying the commutative property for addition here, you can say that 4 + (−7) is the same as (−7) + 4. Notice how this expression is very different than 7 – 4.

 

 

Now look at some multiplication examples.

 

 

 

Commutative Property of Multiplication

For any real numbers a and b, a · b = b · a.

 

Order does not matter as long as the two quantities are being multiplied together. This property works for real numbers and for variables that represent real numbers.

 

Just as subtraction is not commutative, neither is division commutative. 4 ÷ 2 does not have the same quotient as 2 ÷ 4.

 

 

 

 

Rewrite 52 • y in a different way, using the commutative property of multiplication. Note that y represents a real number.   A) 5y • 2   B) 52y   C) 26 • 2 • y   D) y • 52   Show/Hide Answer A) 5y • 2 Incorrect. You cannot switch one digit from 52 and attach it to the variable y. The correct answer is y • 52.   B) 52y Incorrect. This is another way to rewrite 52 • y, but the commutative property has not been used. The correct answer is y • 52.   C) 26 • 2 • y Incorrect. You do not need to factor 52 into 26 · 2. The correct answer is y • 52.   D) y • 52 Correct. The order of factors is reversed.

 

 

 

The associative property of addition states that numbers in an addition expression can be grouped in different ways without changing the sum. You can remember the meaning of the associative property by remembering that when you associate with family members, friends, and co-workers, you end up forming groups with them.

 

Below, are two ways of simplifying the same addition problem. In the first example, 4 is grouped with 5, and 4 + 5 = 9.

 

4 + 5 + 6 = 9 + 6 = 15

 

Here, the same problem is worked by grouping 5 and 6 first, 5 + 6 = 11.

 

4 + 5 + 6 = 4 + 11 = 15

 

In both cases, the sum is the same. This illustrates that changing the grouping of numbers when adding yields the same sum.

 

Mathematicians often use parentheses to indicate which operation should be done first in an algebraic equation. The addition problems from above are rewritten here, this time using parentheses to indicate the associative grouping.

 

(4 + 5) + 6 = 9 + 6 = 15

 

4 + (5 + 6) = 4 + 11 = 15

 

It is clear that the parentheses do not affect the sum; the sum is the same regardless of where the parentheses are placed.

 

Associative Property of Addition

For any real numbers a, b, and c, (a + b) + c = a + (b + c).

 

The example below shows how the associative property can be used to simplify expressions with real numbers.

 

 

 

 

Multiplication has an associative property that works exactly the same as the one for addition. The associative property of multiplication states that numbers in a multiplication expression can be regrouped using parentheses. For example, the expression below can be rewritten in two different ways using the associative property.

Original expression:

 

Expression 1:

 

Expression 2:

 

The parentheses do not affect the product, the product is the same regardless of where the parentheses are.

 

Associative Property of Multiplication

For any real numbers a, b, and c, (a • b) • c = a • (b • c).

 

 

Rewrite  using only the associative property.   A)   B)   C)   D)   Show/Hide Answer A) Correct. Here, the numbers are regrouped. Now  and  are grouped in parentheses instead of  and 6.   B) Incorrect. The order of numbers is not changed when you are rewriting the expression using the associative property of multiplication. How they are grouped should change. The correct answer is .   C)   Incorrect. The order of numbers is not changed when you are rewriting the expression using the associative property of multiplication. Only how they are grouped should change. The correct answer is .   D)   Incorrect. Multiplying within the parentheses is not an application of the property. The correct answer is .

 

 

 

You will find that the associative and commutative properties are helpful tools in algebra, especially when you evaluate expressions. Using the commutative and associative properties, you can reorder terms in an expression so that compatible numbers are next to each other and grouped together. Compatible numbers are numbers that are easy for you to compute, such as 5 + 5, or 3 · 10, or 12 – 2, or 100 ÷ 20. (The main criteria for compatible numbers is that they “work well” together.) The two examples below show how this is done.

 

 

 

 

 

 

Simplify the expression: −5 + 25 – 15 + 2 + 8   A) 5   B) 15   C) 30   D) 55     Show/Hide Answer A) 5 Incorrect. When you use the commutative property to rearrange the addends, make sure that negative addends carry their negative signs. The correct answer is 15.   B) 15 Correct. Use the commutative property to rearrange the expression so that compatible numbers are next to each other, and then use the associative property to group them.   C) 30 Incorrect. Check your addition and subtraction, and think about the order in which you are adding these numbers. Use the commutative property to rearrange the addends so that compatible numbers are next to each other. The correct answer is 15.   D) 55 Incorrect. It looks like you ignored the negative signs here. When you use the commutative property to rearrange the addends, make sure that negative addends carry their negative signs. The correct answer is 15.

 

 

 

The distributive property of multiplication is a very useful property that lets you rewrite expressions in which you are multiplying a number by a sum or difference. The property states that the product of a sum or difference, such as 6(5 – 2), is equal to the sum or difference of products, in this case, 6(5) – 6(2).

 

                                    6(5 – 2) = 6(3) = 18

                                    6(5) – 6(2) = 30 – 12 = 18

 

The distributive property of multiplication can be used when you multiply a number by a sum. For example, suppose you want to multiply 3 by the sum of 10 + 2.

 

3(10 + 2) = ?

 

According to this property, you can add the numbers 10 and 2 first and then multiply by 3, as shown here: 3(10 + 2) = 3(12) = 36. Alternatively, you can first multiply each addend by the 3 (this is called distributing the 3), and then you can add the products. This process is shown here.

 

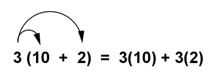
3 (10 + 2) = 3(12) = 36

 

3(10) + 3(2) = 30 + 6 = 36

 

The products are the same.

 

Since multiplication is commutative, you can use the distributive property regardless of the order of the factors.

 

 

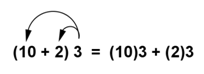
The Distributive Properties

For any real numbers a, b, and c:

Multiplication distributes over addition:           a(b + c) = ab + ac

Multiplication distributes over subtraction:      a(b – c) = ab – ac

 

 

Rewrite the expression 10(9 – 6) using the distributive property.   A) 10(6) – 10(9)   B) 10(3)   C) 10(6 – 9)   D) 10(9) – 10(6)   Show/Hide Answer A) 10(6) – 10(9) Incorrect. Since subtraction isn’t commutative, you can’t change the order. The correct answer is 10(9) – 10(6).   B) 10(3) Incorrect. This is a correct way to find the answer. But the question asked you to rewrite the problem using the distributive property. The correct answer is 10(9) – 10(6).   C) 10(6 – 9) Incorrect. You changed the order of the 6 and the 9. Note that subtraction is not commutative and you did not use the distributive property. The correct answer is 10(9) – 10(6).   D) 10(9) – 10(6) Correct. The 10 is correctly distributed so that it is used to multiply the 9 and the 6 separately.

 

 

 

As long as variables represent real numbers, the distributive property can be used with variables. The distributive property is important in algebra, and you will often see expressions like this: 3(x – 5). If you are asked to expand this expression, you can apply the distributive property just as you would if you were working with integers.

 

3 (x – 5 ) = 3(x) – 3(5) = 3x – 15

 

Remember, when you multiply a number and a variable, you can just write them side by side to express the multiplied quantity. So, the expression “three times the variable x” can be written in a number of ways: 3x, 3(x), or 3 · x.

 

 

 

 

 

 

In the example above, what do you think would happen if you substituted x = 2 before distributing the 5? Would you get the same answer of 5? The example below shows what would happen.

 

 

 

 

 

The distributive property can also help you understand a fundamental idea in algebra: that quantities such as 3x and 12x can be added and subtracted in the same way as the numbers 3 and 12. Let’s look at one example and see how it can be done.

 

 

 

 

Do you see what happened? By thinking of the x as a distributed quantity, you can see that 3x + 12x = 15x. (If you’re not sure about this, try substituting any number for x in this expression…you will find that it holds true!)

 

Groups of terms that consist of a coefficient multiplied by the same variable are called “like terms”. The table below shows some different groups of like terms:

 

 

Whenever you see like terms in an algebraic expression or equation, you can add or subtract them just like you would add or subtract real numbers. So, for example,

10y + 12y = 22y, and 8x – 3x – 2x = 3x.

 

Be careful not to combine terms that do not have the same variable: 4x + 2y is not 6xy!

 

 

 

 

Simplify: 12x – x + 2x – 8x.   A) 23x   B) 5   C) 5x   D) x     Show/Hide Answer A) 23x Incorrect. It looks like you added all of the terms. Notice that −x and −8x are negative. The correct answer is 5x.   B) 5 Incorrect. You combined the integers correctly, but remember to include the variable too! The correct answer is 5x.   C) 5x Correct. When you combine these like terms, you end up with a sum of 5x.   D) x Incorrect. It looks like you subtracted all of the terms from 12x. Notice that −x and −8x are negative, but that 2x is positive. The correct answer is 5x.

 

 

 

The commutative, associative, and distributive properties help you rewrite a complicated algebraic expression into one that is easier to deal with. When you rewrite an expression by a commutative property, you change the order of the numbers being added or multiplied. When you rewrite an expression using an associative property, you group a different pair of numbers together using parentheses. You can use the commutative and associative properties to regroup and reorder any number in an expression as long as the expression is made up entirely of addends or factors (and not a combination of them). The distributive property can be used to rewrite expressions for a variety of purposes. When you are multiplying a number by a sum, you can add and then multiply. You can also multiply each addend first and then add the products together. The same principle applies if you are multiplying a number by a difference.