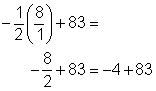Multiplying and Dividing Real Numbers

 

Learning Objective(s)

·         Multiply two or more real numbers.

·         Simplify by using the identity property of 1.

·         Divide real numbers.

·         Solve application problems requiring multiplication or division of real numbers.

 

Introduction

 

After addition and subtraction, the next operations you learned how to do were multiplication and division. You may recall that multiplication is a way of computing “repeated addition,” and this is true for negative numbers as well.

 

Multiplication and division are inverse operations, just as addition and subtraction are. You may recall that when you divide fractions, you multiply by the reciprocal.

 

 

Multiplying Real Numbers

 

Multiplying real numbers is not that different from multiplying whole numbers and positive fractions. However, you haven't learned what effect a negative sign has on the product.

 

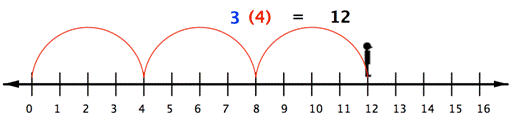
With whole numbers, you can think of multiplication as repeated addition. Using the number line, you can make multiple jumps of a given size. For example, the following picture shows the product 3 · 4 as 3 jumps of 4 units each.

 

 

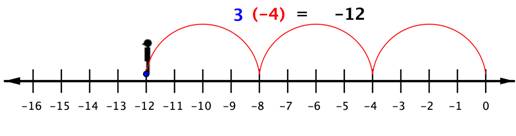
So to multiply 3 (−4), you can face left (toward the negative side) and make three “jumps” forward (in a negative direction).

 

 

 

Use the interactive number line to see how to multiply integers.

 

Sorry, the GeoGebra Applet could not be started. Please make sure that Java 1.4.2 (or later) is installed and active in your browser (Click here to install Java now)

 

The product of a positive number and a negative number (or a negative and a positive) is negative. You can also see this by using patterns. In the following list of products, the first number is always 3. The second number decreases by 1 with each row (3, 2, 1, 0, −1, −2). Look for a pattern in the products of these numbers. What numbers would fit the pattern for the last two products?

 

3(3) = 9

3(2) = 6

3(1) = 3

3(0) = 0

3(−1) = ?

3(−2) = ?

 

Notice that the pattern is the same if the order of the factors is switched:

 

3(3) = 9

2(3) = 6

1(3) = 3

0(3) = 0

−1(3) = ?

−2(3) = ?

 

Take a moment to think about that pattern before you read on.

 

As the factor decreases by 1, the product decreases by 3. So 3(−1) = −3 and 3(−2) = −6.

 

If you continue the pattern further, you see that multiplying 3 by a negative integer gives a negative number. This is true in general.

 

The Product of a Positive Number and a Negative Number.

 

To multiply a positive number and a negative number, multiply their absolute values. The product is negative.

 

You can use the pattern idea to see how to multiply two negative numbers. Think about how you would complete this list of products.

 

−3(3) = −9

−3(2) = −6

−3(1) = −3

−3(0) = 0

−3(−1) = ?

−3(−2) = ?

 

As the factor decreases by 1, the product increases by 3. So −3(−1) = 3, −3(−2) = 6.

 

Multiplying −3 by a negative integer gives a positive number. This is true in general.

 

The Product of Two Numbers with the Same Sign (both positive or both negative).

 

To multiply two positive numbers, multiply their absolute values. The product is positive.

 

To multiply two negative numbers, multiply their absolute values. The product is positive.

 

 

Example

Problem

Find −3.8(0.6).

 

3.8

x 0.6

2.28

Multiply the absolute values as you normally would.

 

Place the decimal point by counting place values.

 

3.8 has 1 place after the decimal point, and 0.6 has 1 place after the decimal point, so the product has 1 + 1 or 2 places after the decimal point.

Answer

−3.8(0.6) = −2.28

The product of a negative and a positive is negative.

 

 

Example

Problem

Find

 

Multiply the absolute values of the numbers.

 

First, multiply the numerators together to get the product's numerator. Then, multiply the denominators together to get the product's denominator. Rewrite in lowest terms, if needed.

Answer

The product of two negative numbers is positive.

 

 

Example

Problem

Find 43y when y = –3.

 

43(−3)

 

43 (3) = 129

Substitute −3 for y in the expression.

 

Multiply 43 and 3.

 

Answer

 

43(−3) = −129

The product of a positive number and a negative number is negative.

 

 

To summarize:

 

positive • positive: The product is positive.

negative • negative: The product is positive.

 

negative • positive: The product is negative.

positive • negative: The product is negative.

 

You can see that the product of two negative numbers is a positive number. So, if you are multiplying more than two numbers, you can count the number of negative factors.

 

Multiplying More Than Two Negative Numbers

 

If there are an even number (0, 2, 4, ...) of negative factors to multiply, the product is positive. If there are an odd number (1, 3, 5, ...) of negative factors, the product is negative.

 

 

Example

Problem

Find 3(−6)(2)( −3)( −1).

 

3(6)(2)(3)(1)

18(2)(3)(1)

36(3)(1)

108(1)

108

Multiply the absolute values of the numbers.

 

3(−6)(2)( −3)( −1)

Count the number of negative factors. There are three (−6, −3, −1).

Answer

3(−6)(2)( −3)( −1) = −108

Since there are an odd number of negative factors, the product is negative.

 

 

Find (−30)( −0.5).

 

A) −150

B) −15

C) 15

D) 150

 

Show/Hide Answer

A) −150

Incorrect. You multiplied 30 and 5 and forgot to adjust the decimal point. You also used the wrong sign. To multiply 30 and 0.5, multiply 30 and 5 to get 150, then place the decimal. Since 0.5 has one digit to the right of the decimal point, the decimal point in the product needs to be placed with one digit to the right of it, to get 15. The two original factors are both negative. Since there is an even number of negative factors, the product is positive. The correct answer is 15.

 

B) −15

Incorrect. You correctly multiplied 30 and 0.5 to get 15, but the two original factors are both negative. Since there is an even number of negative factors, the product is positive. The correct answer is 15.

 

C) 15

Correct. First, multiply 30 and 0.5. Multiply 30 and 5 to get 150, then place the decimal point. Since 0.5 has one digit to the right of the decimal point, the decimal point in the product needs to be placed with one digit to the right of it, to get 15. The two original factors are both negative. Since there is an even number of negative factors, the product is positive.

 

D) 150

Incorrect. First, multiply 30 and 0.5. Multiply 30 and 5 to get 150, then place the decimal point. Since 0.5 has one digit to the right of the decimal point, the decimal point in the product needs to be placed with one digit to the right of it to get 15. The two original factors are both negative. Since there is an even number of negative factors, the product is positive. The correct answer is 15.

 

 

 

The Multiplicative Identity

 

There is a number that can be added, again and again, without ever changing the sum. That number, 0, is called the additive identity.

 

There is also a number that can be included as a factor as many times as you want, and it will never change the value of the product. That number, 1, is called the multiplicative identity.

 

7(1) = 7                       −7(1) = −7

1(3.6) = 3.6                

x(1) = x                       (1)x = x

 

The identity property of 1 states that x(1) = x and (1)x = x.

 

You can think of it in this way: Multiplying by 1 lets the other number keep its identity.

 

 

What is 1(y), when y = −3?

 

A) −3

B) 1

C) 3

 

Show/Hide Answer

A) −3

Correct. Substituting −3 for y gives 1(−3), and 1(−3) = −3.

 

B) 1

Incorrect. The product of a number and 1 is the other number, not 1. Substituting −3 for y gives 1(−3), and 1(−3) = −3.

 

C) 3

Incorrect. The identity property says 1· any number = that number. Substituting −3 for y gives 1(−3), and 1(−3) = −3.

 

 

 

Multiplicative Inverses

 

You might recall that two numbers are additive inverses if their sum is 0, the additive identity.

 

3 and −3 are additive inverses because 3 + (−3) = 0.

 

Two numbers are multiplicative inverses if their product is 1, the multiplicative identity.

 

 and  are multiplicative inverses because .

 

You may remember that when you divided fractions, you multiplied by the reciprocal. Reciprocal is another name for the multiplicative inverse (just as opposite is another name for additive inverse).

 

An easy way to find the multiplicative inverse is to just “flip” the numerator and denominator as you did to find the reciprocal. Here are some examples:

 

The reciprocal of  is  because

The reciprocal of 3 is  because

 

The reciprocal of  is  because

 

The reciprocal of 1 is 1 as 1(1) = 1.

 

 

What is the reciprocal, or multiplicative inverse, of −12?

 

A) −12

B) 1

C)

D) 12

E)

 

Show/Hide Answer

A) −12

Incorrect. −12(−12) = 144, not 1. Since −12 =  and , the correct answer is .

 

B) 1

Incorrect. The reciprocal gives a product of 1; 1 is the reciprocal of 1. Since −12 =  and , the correct answer is .

 

C)

Incorrect. The numerator and denominator are properly "flipped," but the sign is incorrect. The product needs to be positive 1, so since −12 is negative, its reciprocal must also be negative. Since −12 =  and , the correct answer is .

D) 12

Incorrect. 12(−12) = −144, not 1. Since −12 =  and , the correct answer is .

 

E)

Correct. −12 =  and .

 

 

 

Dividing Real Numbers

 

When you divided by positive fractions, you learned to multiply by the reciprocal. You also do this to divide real numbers.

 

Think about dividing a bag of 26 marbles into two smaller bags with the same number of marbles in each. You can also say each smaller bag has one half of the marbles.

 

Notice that 2 and  are reciprocals.

 

Try again, dividing a bag of 36 marbles into smaller bags.

 

 

Number of bags

Dividing by number of bags

Multiplying by reciprocal

3

4

6

 

 

Dividing by a number is the same as multiplying by its reciprocal. (That is, you use the reciprocal of the divisor, the second number in the division problem.)

 

 

Example

Problem

Find

 

Rewrite the division as multiplication by the reciprocal. The reciprocal of  is .

 

Multiply.

Answer

 

 

 

Find . Write the answer in lowest terms.

 

A)

B)

C)

D)

 

Show/Hide Answer

A)

Incorrect. You multiplied without first rewriting the problem using the reciprocal. .

 

B)

Incorrect. You used the reciprocal of the first number (the dividend) rather than the second number you're dividing by (the divisor). .

 

C)

Incorrect. You performed the procedure incorrectly. Rewrite the problem as multiplication, using the reciprocal of the divisor. Then multiply and simplify.

.

 

D)

Correct. Rewrite the problem as multiplication, using the reciprocal of the divisor. Then multiply and simplify. .

 

 

 

Now let's see what this means when one or more of the numbers is negative. A number and its reciprocal have the same sign. Since division is rewritten as multiplication using the reciprocal of the divisor, and taking the reciprocal doesn’t change any of the signs, division follows the same rules as multiplication.

 

Rules of Division

 

When dividing, rewrite the problem as multiplication using the reciprocal of the divisor as the second factor.

 

When one number is positive and the other is negative, the quotient is negative.

 

When both numbers are negative, the quotient is positive.

 

When both numbers are positive, the quotient is positive.

 

 

Example

Problem

Find

 

Rewrite the division as multiplication by the reciprocal.

 

Multiply. Since one number is positive and one is negative, the product is negative.

Answer

 

 

 

Example

Problem

Find  when

 

Substitute  for x in the expression.

 

Rewrite the division as multiplication by the reciprocal.

 

Multiply. There is an even number of negative numbers, so the product is positive.

Answer

 when .

Write the fraction in lowest terms.

 

 

Remember that a fraction bar also indicates division. So, a negative sign in front of a fraction goes with the numerator, the denominator, or the whole fraction: . In each case, the overall fraction is negative because there's only one negative in the division.

 

 

Applications of Multiplication and Division

 

Situations that require multiplication or division may use negative numbers and rational numbers.

 

 

Example

Problem

Carl didn't know his bank account was at exactly 0 when he wrote a series of $100 checks. As each check went through, $125 was charged against his account. (In addition to the $100 for the check, there was a $25 overdraft charge.) After 1 check, his account was −$125 dollars. After 6 of these checks, what was his account balance?

 

−$125(6)

Each check reduces the account by $125; this is represented by −$125. To find the amount it reduces for multiple checks, multiply the number of checks by the amount charged.

 

 

 

Answer

−$125(6) = −$750

 

 

Carl’s account balance is now −$750.

Multiply. Since there is one negative number, the product is negative.

 

 

Example

Problem

Brenda thought she was taking 3 chocolate bars to a picnic with 5 friends. When she brought out the chocolate, she discovered her brother had eaten half of one bar, so she only had  bars to divide among the 6 people (herself and her 5 friends). If each person gets the same amount, how much of a full bar does each person get?

 

Since the candy is being shared among 6 people, divide the amount of chocolate by 6.

 

Rewrite the problem as multiplication, using the reciprocal of the divisor.

 

Change the mixed number to an improper fraction. Multiply.

Answer

Each person gets  of a full bar.

 

 

 

Example

Problem

During a storm, the temperature dropped by  degree every minute. At the beginning of the storm, the temperature was 83°F. An expression giving the temperature t minutes after the storm began is . What was the temperature after 8 minutes?

 

Substitute 8 for t in the expression.

 

First, multiply. You may find it helpful to rewrite 8 as  first.

Notice that since you are multiplying one negative and one positive number, the product is negative.

Finally, add. Use the rules for adding numbers with different signs.

Answer

The temperature was 79°F after 8 minutes.

 

 

Over the course of an 18-year research project, the height of an oceanside cliff actually dropped due to soil erosion. At the end of this period, its height was measured as −3 inches compared to what it had been at the beginning of the research project. What was the average amount that the cliff’s height changed each year?

 

A) −6 in.

B)  in.

C)  in.

D) 6 in.

 

Show/Hide Answer

A) −6 in.

Incorrect. You divided the number of years by the change in height. The correct answer is , or  in.

 

B)  in.

Correct. , or  in.

 

C)  in.

Incorrect. You divided the numerical part correctly, but since you are dividing a negative height by a positive number of years, the answer is negative. The correct answer is , or  in.

 

D) 6 in.

Incorrect. You divided the number of years by the change in height and used the wrong sign. The correct answer is , or  in.

 

 

 

Summary

With multiplication and division, you can find the sign of the final answer by counting how many negative numbers are used in the product or quotient. If there are an even number of negatives, the result is positive. If there are an odd number of negatives, the result is negative. Division can be rewritten as multiplication, by using the reciprocal or multiplicative inverse of the divisor.