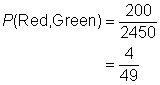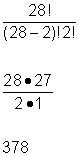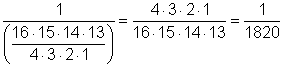Probability of Dependent Events
Learning Objective(s)
· Calculate the probability of dependent events.
Introduction
The probability for any kind of event—simple, compound, independent, dependent—always follows this basic formula:
![]()
The probability is the ratio of the sizes of the event and sample spaces. For some situations, like independent and dependent events, there are ways to calculate these numbers without going through the process of finding and counting possible outcomes one by one, which is sometimes tedious and prone to mistakes.
To find the probability of dependent events, we can use the Fundamental Counting Principle or the permutations and combinations factorial formulas to find the sizes of the event and sample spaces.
| The Fundamental Counting Principle finds the number of permutations and combinations as follows:
When choosing k of n objects, the number of permutations is
When choosing k of n objects, the number of combinations is
The factorial formulas calculate permutations and combinations this way:
When choosing k of n objects, the number of permutations is
When choosing k of n objects, the number of combinations is
|
Finding the event space often requires some extra thought and imagination to identify all of the ways an event can happen.
| Example |
| ||||
| Problem | You pull a marble from a bag with 20 red, 20 white, and 10 green marbles. You hold onto it and then pull another marble. What is the probability of pulling a red marble and then pulling a green marble? |
| |||
|
|
permutation |
| We want to pull a red marble first and then a green marble, so order matters. This is a permutations problem. | ||
|
|
sample space = 2450 |
| The size of the sample space is the number of all possible permutations of 2 marbles. The factorial formula for this is | ||
|
|
Red, Green |
| The size of the event space is the number of all possible combinations for which the first marble is red and the second marble is green. | ||
|
|
20 • 10
event space = 200
|
| How many ways can that happen? Don’t make the mistake of thinking there’s only 1 way: red then green! There are 20 different red marbles that can be chosen first. Then there are 10 different green marbles that can be chosen second. The Fundamental Counting Principle says to multiply these to find the number of ways to get red then green. | ||
|
|
|
| Now the probability that red then green are pulled is the ratio of all the ways to pull those two colors in that order to all the possible permutations. | ||
| Answer | The probability that the pulls are red then green is |
| |||
In finding the event space, it sometimes helps to think of the event we want as removing particular outcomes from individual events. Then we have to find the number of permutations or combinations for the remaining outcomes. In the marble example above, removing a red for the first pull didn’t change the number of green marbles that were available. However, if we wanted the probability of pulling a red and then another red, there are 20 • 19 ways to do that when order matters.
Let’s look at an example involving combinations:
| Example |
| ||||
| Problem | A school organization has 30 members. Four members will be chosen at random for an interview with the school newspaper about the group. What is the probability that Tom and Cindy will be chosen? |
|
| ||
|
|
combination |
| There’s no reason for any person to be considered different from any other, based on the order chosen, so the event and sample spaces involve combinations rather than permutations. |
| |
|
|
|
| The size of the sample space is the number of all possible combinations of 4 members. The formula for combinations is | ||
|
|
|
| The size of the event space is the number of all possible combinations that include Tom and Cindy. |
| |
|
|
Tom, Cindy, __?__, __?__
Find 2 more people from the remaining 28.
|
| If Tom and Cindy must be chosen, then we already know 2 of our 4 four people. Now the problem is how can we fill those 2 slots from the remaining 28 members? This is a new combinations problem, choosing 2 of 28 members. |
| |
|
|
|
| To use the formula, set n = 28 and k = 2. |
| |
|
|
|
| Now the probability that Tom and Cindy are both chosen is the ratio of the combinations including them to all the possible combinations. |
| |
| Answer | The probability that both Tom and Cindy are chosen is |
|
|
| |
Here’s a little arithmetic tip: it may be easier to simplify the probability fraction by leaving the sample and event sizes in factored form. For example:
![]()
We divide fractions by inverting the divisor and multiplying. Then we can remove common factors in the numerator and denominator:
![]()
![]()
![]()
![]()
| A bag of marbles has 20 red marbles, 20 white marbles, and 10 green marbles. If we pull out three marbles, what is the probability that we pull out exactly two red marbles?
A)
B)
C)
D)
|
Probabilities of Dependent and Independent Events
We've been using the Fundamental Counting Principle and the permutation and combination formulas to calculate the probability of a series of events as a whole. We can also calculate probability one event at a time. We can use the following rule to calculate the probability of independent events:
| If A and B are independent events, P(A and B) = P(A) • P(B).
In general, for any number of independent events, the probability that all the events happen is the product of the probabilities that the individual events happen. |
So we can find the probability of many independent events by finding the probability of each individual event on its own, and then multiplying them all together. Each individual event would have the same probability even if none of the other events occurred.
The probability of dependent events can be found in almost the same way. Consider some of the dependent events we have worked with, like the marbles example above. The probability for that example also involved products:
![]()
If we look at this as three separate events, what are the individual probabilities?
First pull:![]()
Second pull: ![]()
Third pull: ![]()
Notice the product of these individual probabilities:
![]()
This is the same result! So we are able to calculate the probability of a series of dependent events by finding the probability of each individual event and then multiplying them all together. But, the individual probabilities are not the same as if the individual events were occurring alone, as was the case for independent events. With dependent events, the probabilities for later events are different than they would have been if they occurred alone.
| If A and B are dependent events, P(A and B) = P(A) • P(B after A) where P(B after A) is the probability that B occurs after A has occurred.
In general, for any number of independent events, the probability that all the events happen is the product of the probabilities that the individual events happen, provided the occurrence of an earlier event is included when finding the probabilities of later events. |
Let's try this method on a problem:
| Example | ||||
| Problem | You accidentally sit on your cellphone, and every time you shift your weight, it randomly dials a different number from your phone book. You have 16 numbers stored, and 4 of those are called before you stand up. What’s the probability that Mary, Lulu, Bo, and Dan all got a phone call? |
| ||
|
| Mary is called Lulu is called Bo is called Dan is called |
| First let’s define the individual events. Order does not matter. | |
|
|
|
| Now let's figure out the probability of each event. For the first call, there are 4 numbers in the event space and 16 numbers to choose from. If the first call does go to Mary, Lulu, Bo, or Dan, for the second call there will be 3 chances to call someone in the event and 15 remaining numbers that could possible be called. For the 3rd call, there are 2 choices from the 14 remaining numbers, and then only 1 out of 13 numbers for the last call.
Use these numbers to find the probabilities of each call. | |
|
|
|
| The probability that all four individual events occur is the product of the individual probabilities. | |
|
|
|
| Let’s find the probability again using the combinations formula. We want a combination because the order doesn’t matter. | |
|
|
|
| The sample space is the number of combinations of 4 phone numbers from 16. Here, k = 4 and n = 16. | |
|
|
|
| The event space is the number of combinations for choosing 4 out of 4 phone numbers. There is only 1 way to do that—all 4 are called! We can check this with the formula (remember that 0! = 1). | |
|
|
|
| The probability is the ratio of the event and sample sizes.
Notice that the result is the same we got for calculating individually. | |
| Answer |
|
|
| |
| A group of eight friends are playing a board game in which the players race to the last spot on the board. The friends agree to play for first, second, and third place.
Assuming all the players are equally matched (so who wins is completely random), what is the probability that Juanita will place first, and then either Bill or Susan places second and either Bill or Susan places third?
A)
B)
C)
D)
|
Summary
There are several ways to find the probabilities of dependent events. The sequence of events can be treated as a whole, in which case the Fundamental Counting Principle or the permutations and combinations formulas are used to find the sizes of the event and sample spaces.
Or each event can be treated separately, in which case the probabilities of each event are multiplied to find the probability of the entire chain of events:
If A and B are dependent events, P(A and B) = P(A) • P(B after A) where P(B after A) is the probability that B occurs after A has occurred.
Regardless of method, it's important to note that when events are dependent, the size of both the event and sample spaces can change over time, because the occurrence of one event affects the outcomes of later events.