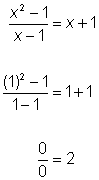Entendiendo Declaraciones Lógicas
Objetivos de Aprendizaje
· Identificar la hipótesis y la conclusión de una declaración lógica.
· Determinar si una declaración matemática que implica ecuaciones lineales, cuadráticas, expresiones de valor absoluto, o desigualdades es verdadera siempre, a veces o nunca.
· Usar contraejemplos para mostrar que una declaración es falsa, y reconocer que un sólo contraejemplo es suficiente.
Introducción
La lógica es una parte esencial del estudio de las matemáticas. Gran parte de las matemáticas tiene que ver con las características de los números y otros objetos (como figuras geométricas o variables), y ser capaz de tomar decisiones sobre qué debe ser verdad basado en características conocidas y otros hechos.
Una declaración lógica es una declaración que, cuando es verdadera, nos permite tomar un conjunto de hechos y deducir (o suponer) un nuevo hecho a partir de ellos. Las declaraciones lógicas tienen dos partes: hipótesis, que es la premisa o conjunto de hechos con los que empezamos, y la conclusión, que es el nuevo hecho que podemos deducir cuando la hipótesis es verdadera. (Nota: Si has usado las hipótesis en la clase de ciencias, probablemente ya has notado que esta es una definición diferente. ¡Ten cuidado de no confundirte!)
Considera la siguiente declaración:
Si sales de casa sin ningún tipo de equipo o ropa para lluvia cuando está lloviendo, te vas a mojar.
Aquí, la hipótesis es "sales de casa sin ningún tipo de equipo o ropa para lluvia cuando está lloviendo." La hipótesis debe ser completamente verdadera antes de que la podemos usar para deducir algo nuevo a partir de ella. ¿Qué dice esta declaración sobre alguien que no sale de su casa? ¿Y sobre alguien que usa un paraguas? ¿O qué pasa si no está lloviendo? Nada. Esta declaración no aplica a ninguno de esos casos.
La conclusión de esta declaración es "te vas a mojar." Supón que está lloviendo, y que alguien sale de casa, y no trae ningún equipo para lluvia u otro aditamento — ¿qué pasará? Todas las partes de la hipótesis se han cumplido, entonces — si la declaración es verdadera — podemos deducir que la persona se va a mojar, ¡Suena razonable!
Nota que en este ejemplo, si la hipótesis no es verdadera, la persona podría mojarse, En un día soleado sin lluvia, alguien podría salir para lavar su carro y mojarse con la manguera. Otra persona podría ir a nadar, ¡y entonces se mojaría bastante! La declaración no dice nada cuando la hipótesis es falsa. Sólo es útil cuando la hipótesis es verdadera.
No todas las declaraciones lógicas están escritas como "Si (algo es verdadero) entonces (algo más es verdadero)." Para identificar la hipótesis y la conclusión, podrías reescribir la declaración en un formato "si-entonces."
| Ejemplo | |||
| Problema | Identificar la hipótesis y la conclusión en la declaración, “Me duele la cabeza cada vez que duermo más de 9 horas.” |
|
|
|
| Si duermo más de 9 horas, entonces me duele la cabeza |
| Esta declaración no está escrita como una declaración "si-entonces", entonces puedes escribirla en esos términos. ¡Asegúrate de que la nueva declaración diga esencialmente lo mismo que la original! |
| Solución | Hipótesis: Duermo más de 9 horas |
| La hipótesis es la parte "si" de la declaración |
|
| Conclusión: Me duele la cabeza
|
| La conclusión es la parte "entonces" de la declaración |
Las declaraciones lógicas también pueden ser sobre las matemáticas. Cualquier cosa que nos permita deducir un nuevo hecho sobre algo matemático dada cierta información es una declaración lógica. Por ejemplo, "Las diagonales de un rectángulo tienen la misma longitud" es una declaración lógica. La hipótesis es la parte que nos puede ayudar si sabemos que es verdadera. ¿Cuándo podría ser útil esta declaración?
| Ejemplo | |||
| Problema | Identificar la hipótesis y la conclusión en la declaración, “Las diagonales de un rectángulo tienen la misma longitud.” |
|
|
|
|
Si una figura es un rectángulo, entonces sus diagonales tienen la misma longitud |
| Reescribirla en la forma si-entonces
En esta declaración, que la figura sea un rectángulo es la información dada, y la igualdad de las diagonales es el nuevo hecho que se deduce del hecho conocido |
| Solución | Hipótesis: una figura es un rectángulo |
|
|
|
| Conclusión: las diagonales tienen la misma longitud
|
|
|
Con declaraciones algebraicas, la hipótesis es a menudo una suposición sobre qué valores están permitidos para una variable. Por ejemplo, puede que hayas visto una declaración como esta "a + b = b + a, donde a y b son números reales." Vamos a tratar esta ecuación como una declaración lógica:
| Ejemplo | |||
| Problema | Identificar la hipótesis y la conclusión en la declaración, “a + b = b + a, donde a y b son números reales.” |
|
|
|
| Si a y b son números reales, entonces a + b = b + a
|
| Reescribirla en la forma si-entonces |
| Solución | Hipótesis: a y b son números reales |
| La hipótesis es la parte "si" de la declaración |
|
| Conclusión: a + b = b + a
|
| La conclusión es la parte "entonces" de la declaración |
| Considera esta declaración:
|x| ≥ 0 para todos los números reales x.
¿Cuál de los siguientes enunciados identifica mejor la hipótesis y la conclusión de la declaración?
A) La hipótesis es “|x| ≥ 0” y la conclusión es “todos los números reales x.” B) La hipótesis es “x es un número real” y la conclusión es “|x| ≥ 0.” C) La hipótesis es “todos los números reales x” y la conclusión es “|x| ≥ 0.” D) La hipótesis es “|x| ≥ 0” y la conclusión es “para todos los números reales.”
|
El pensamiento crítico es importante, no sólo en matemáticas sino en la vida diaria. ¿Alguna vez has escuchado a alguien hacer una declaración y luego piensas, "Un momento. ¿Es cierto eso?"? Algunas veces la gente tiene razones para pensar que algo es cierto aunque no lo sea. ¡Poder determinar si una declaración es cierta es una habilidad valiosa!
Cuando hay que determinar si una declaración es verdadera, la mayoría de las personas empiezan por buscar ejemplos, que son situaciones en donde la declaración resulta ser verdadera (la hipótesis y la conclusión son verdaderas). Una situación más útil que podemos encontrar, si existe, es un contraejemplo, una situación para la que la hipótesis es verdadera, pero la conclusión es falsa). ¿Por qué son tan poderosos los contraejemplos?
Considera una persona que ve la luna muchas veces en la noche y piensa: "Nunca he visto la luna durante el día." La persona podría entonces hacer la declaración, "La luna sólo sale de noche." Como una declaración si-entonces, es lo mismo que decir "Si sale la luna, es que es de noche." Probablemente podemos pensar en muchas veces cuando vimos a la luna salir, y era de noche. Estos son ejemplos, situaciones cuando la declaración fue verdadera.
Pero de hecho, la declaración no es siempre verdadera, y sólo necesitamos ver la luna durante el día una vez — sólo un contraejemplo — para saber que la declaración es falsa. Muchos, muchos ejemplos no pueden probar que la declaración es verdadera, ¡pero sólo necesitamos un contraejemplo para probar que no lo es!
Para una declaración dada, tenemos tres posibilidades:
| La veracidad de las declaraciones lógicas
Una declaración es: si:
Siempre verdadera Existen ejemplos pero no contraejemplos.
A veces verdadera Existe por lo menos un ejemplo y por lo menos un contraejemplo.
Nunca verdadera No hay ejemplos, sólo contraejemplos. |
Entonces, ¿cómo podemos estar seguros de que algo es verdadero (o nunca lo es), si no podemos basarnos en muchos ejemplos? Con las declaraciones algebraicas, algunas veces podemos acudir a una gráfica:
| Ejemplo | |||
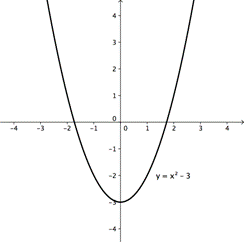
| Problema | ¿Es verdadera la siguiente declaración, siempre, a veces o nunca?
x2 – 3 > -4, para todos los números reales x |
| |
|
|
| Graficar la ecuación | |
|
|
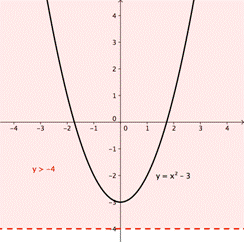
| Nota donde y > -4.
Toda la gráfica está en la región donde y > -4, por lo que la declaración es siempre verdadera | |
| Solución |
siempre verdadera |
|
|
Otra forma de decidir si algo es verdadero siempre, a veces, o nunca es razonando a partir de otras cosas que sabemos que son ciertas. Podemos empezar con algo que sabemos es verdadero e intentar llegar la declaración original. Intentemos esto con el ejemplo anterior.
| Ejemplo | |||
| Problema | ¿Es verdadera la siguiente declaración, siempre, a veces o nunca?
x2 – 3 > -4, para todos los números reales x |
|
|
|
|
x2 ≥ 0, para todos los números reales x |
| La conclusión es una desigualdad que incluye a x2. Sabemos que x2 es siempre positivo o 0 para todos los números reales x
Ahora usaremos álgebra para hacer que esta declaración se vea parecida a la declaración original. Esto podría requerir más de un paso |
|
| x2 − 3 ≥ -3, para todos los números reales x |
| Primero, restar 3 en ambos lados |
|
| x2 − 3 ≥ -3 > -4, para todos los números reales x |
| Luego notar que t -3 > -4. |
|
| x2 − 3 > -4, para todos los números reales x |
| ¡Esto significa que la declaración original es siempre verdadera! |
| Solución | siempre verdadera |
|
|
Cuando tratamos de relacionar argumentos lógicos, el problema más grande puede ser dónde comenzar. Es muy probable que nuestros primeros intentos lleguen a un callejón sin salida, y tendremos que volver a empezar. La práctica lo hace más fácil, Algunas veces ayuda trabajar hacia atrás: empezar asumiendo que la conclusión es verdadera, intentando pensar en una declaración relacionada que sea verdadera (o falsa), y luego conectarlas. Echemos un último vistazo al problema anterior.
| Ejemplo | |||
| Problema | ¿Es verdadera la siguiente declaración, siempre, a veces o nunca?
x2 − 3 > -4, para todos los números reales x |
|
|
|
|
Si x2 − 3 > -4, para todos los números reales x… |
| Si no sabes por dónde empezar, asume que la conclusión es verdadera |
|
| Entonces x2 > -1, para todos los números reales x |
| Ahora busca algo que sabes que es verdadero. Normalmente esto significa simplificar expresiones o resolver ecuaciones. En este caso, suma 3 a ambos lados para obtener x2 despejada |
|
| No sólo x2 > -1, x2 ≥ 0, lo que es aún mejor (porque 0 > -1). |
| Cuando encuentras algo que sabes que es verdadero (o falso), ¡ya encontraste tu punto de partida! |
|
| x2 ≥ 0, para todos los números reales x.
Eso significa que x2 > -1, para todos los números reales x.
Entonces x2 – 3 > -4, para todos los números reales x.
|
| Ahora que sabes por dónde empezar, puedes trabajar hacia atrás para explicar cómo sabes que la declaración es siempre verdadera |
| Solución |
siempre verdadera |
|
|
Otra forma de probar la veracidad de una declaración es buscar contraejemplos, Las gráficas también nos pueden ayudar a eso:
| Ejemplo | |||
| Problema | ¿Es verdadera la siguiente declaración, siempre, a veces o nunca?
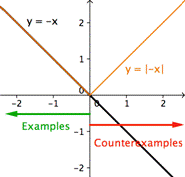
|-x| = -x, para todos los números reales x |
|
|
|
|
|
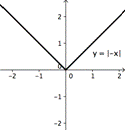
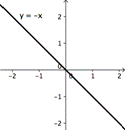
| Graficar ambos lados de la ecuación: y = |-x| y y = -x. |
|
|
Ejemplos (declaración verdadera): x = 0, x = -3
Contraejemplos (declaración falsa): x = 1, x = 100 |
| Como la declaración que estas dos gráficas deberían ser idénticas, los ejemplos salen de cuando coinciden
Los contraejemplos son cuando no coinciden.
Para esta declaración, existe por lo menos un ejemplo y por lo menos un contraejemplo |
| Solución |
Algunas veces verdadera |
|
|
Aunque sabemos que |-x| = -x no siempre es verdadero si x es un número real, también sabemos que algunas veces es cierto, De hecho, podemos especificar cuándo es verdadero — usando la gráfica del ejemplo, podemos ver que es verdadero cuando x ≤ 0. Podemos usar ese hecho para crear una nueva declaración:
Si x ≤ 0, entonces |-x| = -x.
Como la hipótesis es más específica, la declaración es siempre verdadera.
| ¿Es verdadera la siguiente declaración, siempre, a veces o nunca?
-2x2 + 8x + 10 > 18, para todos los números reales x
A) Siempre B) A veces C) Nunca
|
Casos Especiales
Cuando buscamos ejemplos, y particularmente cuando buscamos contraejemplos, hay algunos casos especiales que son fáciles de pasar por alto. Tener en cuenta estos casos es normalmente muy útil. Revisa algunos casos especiales y considera si alguno de ellos provee un contraejemplo para la siguiente declaración: "Cuando dos números se multiplican, el producto es mayor que cada uno de los factores."
| Casos especiales para ejemplos y contraejemplos
Ten en cuenta estos casos cuando determines si una declaración matemática es verdadera siempre, a veces, o nunca. | |
| Cero | El cero puede ser un problema en los siguientes tipos de expresiones: - Expresiones racionales (ya que el denominador no puede ser 0) - Expresiones con exponentes (si la base es 0, el exponente no puede ser negativo o 0, y con exponentes positivos la expresión se evalúa como 0, si la base no es 0, pero sí el exponente, la expresión se evalúa como 1) - Expresiones con raíces pares (sólo hay una raíz y no dos) - Expresiones con valores absolutos (la única vez que el valor absoluto no es positivo es cuando la expresión dentro del signo de valor absoluto es 0)
|
| Números negativos | Estos pueden ser un problema en los siguientes tipos de expresiones: - Expresiones con raíces impares (un número negativo no tiene raíces de números reales) - Expresiones con exponentes (si el exponente es negativo, la base no puede ser 0, si el exponente es una fracción con un denominador par — indicando una raíz par — la base no puede ser negativa, si la base es negativa y exponente varía, el valor de la expresión puede cambiar entre negativo para los exponentes impares y positivo para los exponentes pares) - Expresiones con valores absolutos (si x es positivo o 0, entonces |x| = x, pero si x es negativo, entonces |x| = -x, esto es, el valor absoluto es el opuesto de x)
|
| Fracciones | Las fracciones pueden presentar problemas en los siguientes casos: - Cuando sólo respuestas con números enteros tienen sentido, como en preguntas sobre objetos indivisibles (por ejemplo, gente o vehículos) - Expresiones con exponentes (como los exponente fraccionarios pueden ser interpretados como raíces, bases negativas pueden ser un problema)
|
| Fracciones entre | Si bien las fracciones se mencionaron anteriormente, estas son importantes de forma diferente. - Cuando multiplicamos, el producto de dos números mayores a 1 el producto siempre será mayor que cualquiera de los números. Sin embargo, si por lo menos uno de esos números está entre 0 y 1, este no es el caso. (Por ejemplo, 0.5 • 6 = 3, que es mayor que 0.5 pero menor que 6.) - Las expresiones con exponentes tienen un problema similar. Una base mayor a 1 dará un resultado mayor que la base cuando se toma una potencia mayor que 1. Sin embargo, si la base está entre 0 y 1, o el exponente está entre 0 y 1, el resultado será más cercano a 0 que la base original. |
Aquí hay algunos ejemplos. Considera los casos especiales anteriores cuando resuelvas estos.
| Ejemplo | |||
| Problema | ¿Es verdadera la siguiente declaración, siempre, a veces o nunca?
|
|
|
|
|
|
| El lado izquierdo es una expresión racional que puede ser simplificada. Empieza por factorizar el numerador |
|
|
|
| El numerador y el denominador tienen el factor común (x – 1), por lo que podemos simplificar la expresión racional |
|
|
|
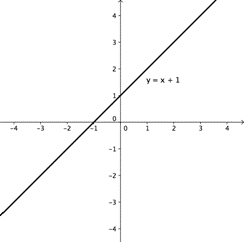
| La expresión simplificada es la misma que la del lado derecho de la declaración original, y la gráfica (hecha con una calculadora graficadora o una computadora) mostrará la misma recta que y = x + 1. Por lo que podemos pensar que la declaración es siempre verdadera |
|
|
|
| Pero veamos uno de nuestros casos especiales, Cuando tenemos una expresión racional, un valor de 0 es razón para pensar cuidadosamente. En este caso, el problema no es que x es 0 sino cuando el denominador, x – 1, es 0. Intenta usar x = 1 en la declaración |
| Solución |
Verdadera algunas veces (verdadera cuando x ≠ 1)
|
| Existe un contraejemplo que vuelve la declaración verdadera algunas veces: x = 1 |
| Ejemplo | |||
| Problema | ¿Es verdadera la siguiente declaración, siempre, a veces o nunca?
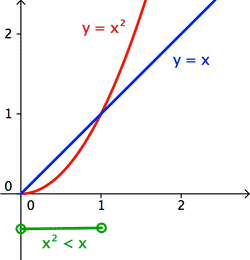
x2 < x, para números reales no negativos (positivos o 0) x |
|
|
|
|
Si x = 0, x2 = 0, entonces x2 = x.
Si x = 1, x2 = 1, entonces x2 = x.
Si x = 2, x2 = 4, entonces x2 > x.
Si x = 10, x2 = 100, entonces x2 > x. |
| Intenta algunos ejemplos. Para estos ejemplos, ¡la declaración es falsa! |
|
|
|
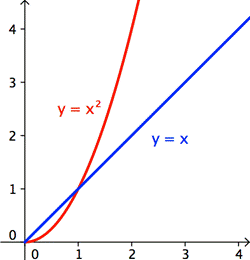
| Veamos las gráficas. Grafica ambos lados de la ecuación: y = x2 y y = x |
|
|
|
| La declaración dice que x2 < x, entonces vemos si en alguna parte de la gráfica de y = x2 está por debajo de la gráfica de y = x.
Cuando x está entre 0 y 1, la gráfica de x2 está por debajo de la gráfica de x |
| Solución |
Verdadera algunas veces (verdadera cuando 0 < x < 1) |
|
|
| ¿Es verdadera la siguiente declaración, siempre, a veces o nunca?
2|x + 3| = 2x + 6, para todos los números reales x
A) Siempre B) Algunas veces C) Nunca
|
Sumario
Las declaraciones lógicas tienen dos partes, la hipótesis que presenta hechos que la declaración considera verdaderos, y la conclusión que presenta un nuevo hecho que podemos deducir cuando la hipótesis es verdadera.
Para que una declaración sea siempre verdadera, no deben existir contraejemplos para los cuales la hipótesis es verdadera y la conclusión es falsa. Si existen ejemplos para los que la declaración es verdadera, pero también hay contraejemplos, entonces la declaración es verdadera a veces. Estas declaraciones verdaderas a veces pueden volverse siempre verdaderas cambiando la hipótesis. Una declaración es falta si no existen ejemplos para los que la hipótesis y la conclusión son verdaderas. Cuando buscamos contraejemplos y ejemplos, existen algunos casos especiales (como con los números negativos y las fracciones) que deberían ser considerados.