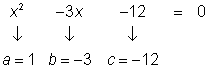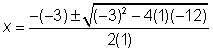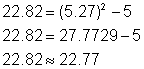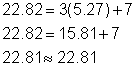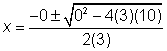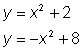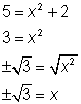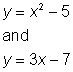Systems of Non-Linear Equations

 

Learning Objective(s)

·         Solve systems of equations involving linear, quadratic, and other non-linear functions.

 

 

A system of equations is a set of two or more equations that share two or more unknowns. The solutions to a system of equations are all the values that make all of the equations true, or the points where the graphs of the equations intersect.

 

We can solve a system of linear equations through graphing, substitution and linear combination. Systems of nonlinear functions, such as quadratic or exponential equations, can be handled with the same techniques.

 

To illustrate how to solve these systems, we'll focus on linear and quadratic systems with just two equations.  But be aware that systems can be larger and more complex than these examples.

 

 

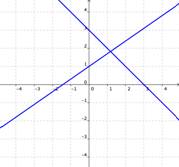
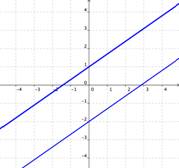
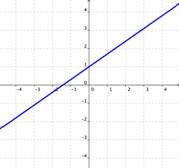
Let’s begin by talking about two linear equations. The solution to this kind of system is the point of intersection between the two lines, or the place where the two equations have the same x and y values. There may be one solution, no solution, or an infinite number of solutions to a system of two linear equations:

 

One Solution	No Solutions	Infinite Solutions
If the graphs of the equations intersect, then there is one solution that is true for both equations.	If the graphs of the equations do not intersect (for example, if they are parallel), then there are no solutions that are true for both equations.	If the graphs of the equations are the same, then there are an infinite number of solutions that are true for both equations.

 

 

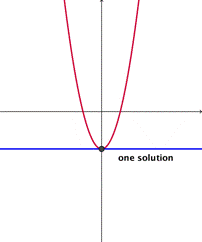
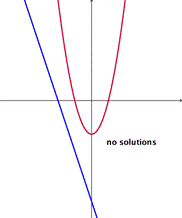
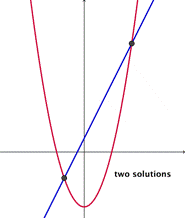
To solve a system of a linear equation and a quadratic equation, we will do the same thing, find the point—or points—of intersection between the two graphs:

 

One Solution	No Solutions	Two Solutions
If the parabola and the line touch at a single point, then there is one solution that is true for both equations.	If the graphs of the equations do not intersect, then there are no solutions that are true for both equations.	If the line intersects the parabola in two places, then there are two solutions that are true for both equations.

 

It does not make sense to consider the case where the two equations represent the same set of points, since a straight line can never be a parabola, and vice versa.

 

Notice that this means the possible number of solutions for a system of two linear equations is 0 (never touch), 1 (cross in one place), or infinity (the lines are identical). The number of solutions for a system with one linear equation and one quadratic equation is either 0 (never touch), 1 (touch in one place), or 2 (cross in two places).

 

Let's solve a system of a linear and a quadratic equation by graphing:

 

 

 

Notice that while we can tell approximately where the two graphs intersect, it is difficult to find an exact location.

 

Now let’s solve the same system using substitution. When solving using substitution, use the following steps: 

 

1. Select one equation and isolate a variable. (Choose an equation and variable which are easy to isolate!)
2. Substitute the resulting expression for a variable into the other equation, every time that variable appears.
3. Solve the second equation for the second variable.
4. Substitute the solution to step 3 into the expression in step 1, to find the other variable.

 

 

By using substitution we have arrived at a more precise answer than we did when graphing this system, however, approximations were made when we took the square root of 57. This still is not an exact solution!

 

As the algebra of substitution can become quite involved, it is always a good idea to check the result in the original equations.

 

Here is a check of the point (5.27, 22.82):

 

 

 

Notice that the check doesn’t result in perfect equality, but it's close.

 

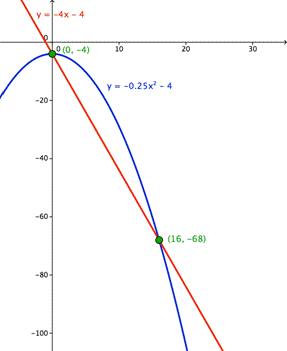
Use graphing to find the number of solutions to the system of equations.                     y = -4x – 4 and y = -0.25x2 – 4   A) one solution B) two solutions C) no solutions D) infinite solutions   Show/Hide Answer The correct answer is B). The graph reveals two solutions.

 

 

Now let’s look at two quadratic equations.  Picture for a moment how the graphs of two quadratic equations can intersect (or not).

 

One Solution	No Solutions
Two quadratic equations that have a single point in common, such as a shared vertex, have one solution.	Two quadratic functions that have no overlap in range (no shared y-values) have no solutions.
Two Solutions	Infinite Solutions
Two quadratic equations that overlap but have different equations have two solutions.	If the graphs of the equations are the same, then there are an infinite number of solutions that are true for both equations.

 

 

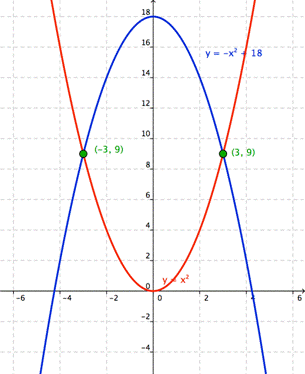
We can solve a system of quadratic equations by graphing:

 

 

Again, we can't be certain by graphing that our solutions are exact. An algebraic method can ensure an exact solution every time. For example, we can solve a system of quadratic equations by substitution:

 

 

 

Since there is no solution, we cannot check our answer algebraically, but we can look at the graphs to verify that there is no solution:

 

 

 

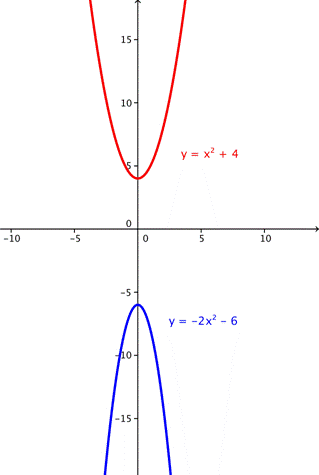
We can also use linear combination to solve systems of equations, following these steps:

 

1. Rearrange equations so the terms line up.
2. Multiply none, or one, or both equations by a constant so that the coefficients of one of the variables are opposites
3. Add the equations to eliminate one of the variables
4. Solve the resulting equation
5. Substitute the solution in step 4 back into an original equation to find the other variable

 

Ready to give that a try?

 

 

 

Solve the system: Find the points of intersection, if any, of the two equations below:   A) no solution, no points of intersection B) C) (1,-4) and (2, -1) D) (-2, 13) and (-1, 4)   Show/Hide Answer A) Incorrect. This system can be solved, and there are many ways to do so. Using substitution, for example, you can substitute one expression for y into the other equation: x2 – 5 = 3x – 7. Subtract 3x and add 7 to both sides to get x2 – 3x + 2 = 0. This can be factored as (x – 2)(x – 1) = 0, so the x values are 1 and 2. Substituting these values into either original equation gives the points (1, -4) and (2, -1).   B) Incorrect. This is the solution to the equation . For a system, you must use both equations in the solution process. Using substitution, for example, you can substitute one expression for y into the other equation: x2 – 5 = 3x – 7. Subtract 3x and add 7 to both sides to get x2 – 3x + 2 = 0. This can be factored as (x – 2)(x – 1) = 0, so the x values are 1 and 2. Substituting these values into either original equation gives the points (1, -4) and (2, -1).   C) Correct. You can solve in many ways. Using substitution, for example, you can substitute one expression for y into the other equation: x2 – 5 = 3x – 7. Subtract 3x and add 7 to both sides to get x2 – 3x + 2 = 0. This can be factored as (x – 2)(x – 1) = 0, so the x values are 1 and 2. Substituting these values into either original equation gives the points (1, -4) and (2, -1).   D) Incorrect. You may have combined the equations correctly, but then factored the result incorrectly to get (x + 2)(x + 1). Substitute one expression for y into the other equation gives x2 – 5 = 3x – 7. Subtract 3x and add 7 to both sides to get x2 – 3x + 2 = 0. This can be factored as (x – 2)(x – 1) = 0 (note that the middle term is -3x, not + 3x), so the x values are 1 and 2. Substituting these values into either original equation gives the points (1, -4) and (2, -1).

 

Solving systems of non-linear equation can be done using the techniques of graphing, substitution and linear combination. Just like with systems of linear equations, when we find solutions to systems of non-linear equations, we are finding the intersection of their graphs or the places where the equations have the same variable values.