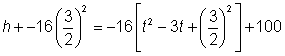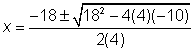Applications of Quadratic Functions
Learning Objective(s)
· Apply quadratic functions to real world situations in order to solve problems.
Introduction
Quadratic functions are more than algebraic curiosities—they are widely used in science, business, and engineering. The U-shape of a parabola can describe the trajectories of water jets in a fountain and a bouncing ball, or be incorporated into structures like the parabolic reflectors that form the base of satellite dishes and car headlights. Quadratic functions help forecast business profit and loss, plot the course of moving objects, and assist in determining minimum and maximum values. Most of the objects we use every day, from cars to clocks, would not exist if someone, somewhere hadn't applied quadratic functions to their design.
We commonly use quadratic equations in situations where two things are multiplied together and they both depend of the same variable. For example, when working with area, if both dimensions are written in terms of the same variable, we use a quadratic equation. Because the quantity of a product sold often depends on the price, we sometimes use a quadratic equation to represent revenue as a product of the price and the quantity sold. Quadratic equations are also used when gravity is involved, such as the path of a ball or the shape of cables in a suspension bridge.
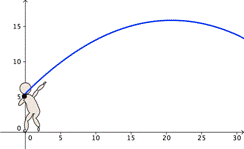
A very common and easy-to-understand application of a quadratic function is the trajectory followed by objects thrown upward at an angle. In these cases, the parabola represents the path of the ball (or rock, or arrow, or whatever is tossed). If we plot distance on the x-axis and height on the y-axis, the distance of the throw will be the x value when y is zero. This value is one of the roots of a quadratic equation, or x-intercepts, of the parabola. We know how to find the roots of a quadratic equation—by either factoring, completing the square, or by applying the quadratic formula.
Let’s look at a throw made by a shot-putter. Notice that x = 0 when the shot-putter has the shot (a heavy metal ball) in his hand—the shot hasn't gone anywhere yet. The shot-putter usually starts with the shot at his shoulder, so y (height) is not 0 when x = 0:
| Example | ||||
| Problem | A shot-put throw can be modeled using the equation
|
| ||
|
|
|
| The throw ends when the shot hits the ground. The height y at that point is 0, so set the equation equal to zero. | |
|
|
|
| This equation is difficult to factor or to complete the square, so we'll solve by applying the quadratic formula, | |
|
|
|
| Simplify. | |
|
|
or
|
| Find both roots. | |
|
|
x ≈ 46.4 or -4.9 |
| Do the roots make sense? The parabola described by the quadratic function has two x-intercepts. But the shot only traveled along part of that curve.
One solution, -4.9, cannot be the distance traveled because it is a negative number.
The other solution, 46.4 feet, must give the distance of the throw. | |
| Answer |
Approximately 46.4 feet |
|
| |
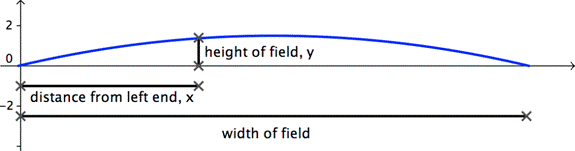
| Although a stadium field of synthetic turf appears to be flat, its surface is actually shaped like a parabola. This is so that rainwater runs off to the sides. If we take a cross section of the turf, the surface can be modeled by
A) 80 ft B) 1.5 ft C) 234 ft D) 160 ft
|
Finding the Maximum and Minimum
Another common use of the quadratic equation in real world applications is to find maximum (the most or highest) or minimum (the least or lowest) values of something. Recall that the vertex is the turning point of a parabola. For a parabola opening downward, the vertex is the high point, which occurs at the maximum possible y value. For a parabola opening upward, the vertex is the lowest point of the parabola, and occurs at the minimum y value.
To use a quadratic equation to find a maximum or minimum, we usually want to put the quadratic equation into the vertex form of a quadratic equation, ![]() . This lets us quickly identify the coordinates of the vertex (h, k).
. This lets us quickly identify the coordinates of the vertex (h, k).
Let's see how this works by trying a motion problem. The equation ![]() is commonly used to model an object that is launched or thrown. The variable h represents the height in feet, and t represents the time in seconds. The other two values are usually given numbers: h0 is the initial height in feet and v0 is the initial velocity in feet/second.
is commonly used to model an object that is launched or thrown. The variable h represents the height in feet, and t represents the time in seconds. The other two values are usually given numbers: h0 is the initial height in feet and v0 is the initial velocity in feet/second.
When working with this equation, we assume the object is in “free fall”, which means it is moving under the sole influence of gravity. There is no air resistance or any other interference of any kind (not so likely in the real world, but still, these equations are quite helpful).
| Example | ||||
| Problem | A ball is launched upward at 48 ft/s from a platform that is 100 ft. high. Find the maximum height the ball reaches and how long it will take to get there. |
| ||
|
|
| Start with the equation that models an object being launched or thrown | ||
|
|
| Substitute the initial velocity v0 = 48 and height h0 = 100. | ||
|
|
| Since we want to get the vertex form of the equation, a(x – h)2, factor -16 out of the first two terms. The value of a is -16 and we will use t for x. That way we can complete the square on t2 – 3t to get the equation in vertex form. | ||
|
|
| Remember that when we complete the square, we add a value to the expression. Because of the coefficient on the t2 term, this can get a little confusing, so we are going to prepare to complete the square for t2 – 3t by adding c to t2 – 3t, inside the parentheses.
When we add a quantity to one side of the equation, we must also add it to the other side. Because the quantity added, c, is inside the parenthesis on the right, we are actually adding -16c. This means when we add the quantity to the left side, we must add -16c. | ||
|
|
| To complete the square on x2 + bx, we add | ||
|
|
| Simplify, writing the square of the binomial on the right and | ||
|
|
| Add 36 to both sides. We now have the vertex form, and can identify the vertex as
The x-coordinate is t in this equation, which stands for time. The y-coordinate represents height. | ||
| Answer |
The maximum height is 136 feet and it will take 1.5 seconds to reach this height |
|
| |
We could have found the vertex by using other methods, such as by graphing or by using the formula ![]() to find the x-coordinate of the vertex, then substitute that x-value into the original formula to get the y-value of the vertex).
to find the x-coordinate of the vertex, then substitute that x-value into the original formula to get the y-value of the vertex).
| A farmer has 1000 feet of fencing and a very big field. She can enclose a rectangular area with dimensions x ft and 500 – x ft. What is the largest rectangular area she can create?
A) 62,500 ft2 B) 250,000 ft2 C) 1,000 ft2 D) 500 ft2
|
Modeling a Situation
Quadratic equations are sometimes used to model situations and relationships in business, science and medicine. A common use in business is to maximize profit, that is, the difference between the total revenue (money taken in) and the production costs (money spent).
The relationship between the cost of an item and the quantity sold is often linear. In other words, for each $1 increase in price there is a corresponding decrease in quantity sold. (Think about it: if the price of something goes up, do you buy more or less? Hopefully less!) Once we determine a relationship between the selling price of an item and the quantity sold, we can think about how to generate the most profit. At what selling price do we make the most money?
The amount of profit will be found by taking the total revenue (the quantity sold multiplied by the selling price) and subtracting the cost to produce the all the items: Profit = Total Revenue – Production Costs. We can integrate the linear relationship of selling price to quantity and the Profit formula and create a quadratic equation, which we can then maximize. Let’s look at an example:
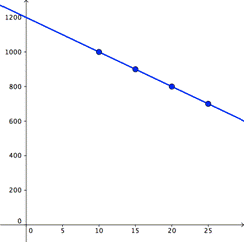
Here is a sample data set:
| Selling Price $ (s) | Quantity Sold in 1 year (q) |
| 10 | 1000 |
| 15 | 900 |
| 20 | 800 |
| 25 | 700 |
In order to calculate the profit, we also need to know how much it costs to produce each item. For this example, the cost to produce each item is $10.
| Example | |||
| Problem | Using the data given above, determine the selling price s, which produces the maximum yearly profit. |
| |
|
|
q = -20s + 1200
q = quantity sold s = selling price of the item
|
| Plot s on the horizontal axis and q on the vertical axis. Use any two of the points on the straight line of the plot to find the slope of the line to be -20. Read the y-intercept as 1200.
Put these values into slope-intercept form (y = mx + b): q = -20s + 1200
|
|
|
P = sq – 10q
|
| Profit formula is P = Total Revenue – Production Costs
Total Revenue = price • quantity sold
Production Costs = cost per item • quantity sold
So P = sq – 10q |
|
|
P = s(-20s + 1200) – 10(-20s + 1200) |
| Substitute -20s + 1200 for q in profit formula. |
|
|
P = -20s2 + 1200s + 200s – 12000
P = -20s2 + 1400s – 12000 |
| Multiply the expressions and combine like terms. We now have a quadratic function.
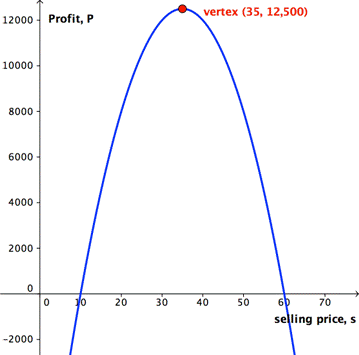
By finding the vertex of the parabola, we will find the selling price that will generate the most profit. The x-axis represents selling price, so the value of the x-coordinate at the vertex represents the best price.
The y-value at the vertex will give the amount of profit made. |
|
|
|
| Find the x-coordinate of the vertex by applying the formula |
| Answer |
The selling price that generates the maximum profit is $35 |
|
|
Here is a graph of the profit function, showing the vertex:
Next is a word problem you may not think is a quadratic equation. The area problem below does not include a quadratic formula of any type and the problem seems to be something you have solved many times before by simply multiplying. But in order to solve it, you will need to use a quadratic equation.
| Example | |||
| Problem |
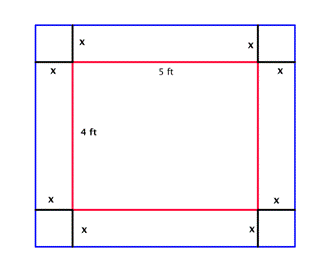
Bob made a quilt that is 4 ft x 5 ft. He has 10 sq. ft. of fabric to create a border around the quilt. How wide should he make the border to use all the fabric? (The border must be the same width on all four sides.)
| ||
|
|
| Sketch the problem. Since we don’t know the width of the border, we give it the variable x. | |
|
|
|
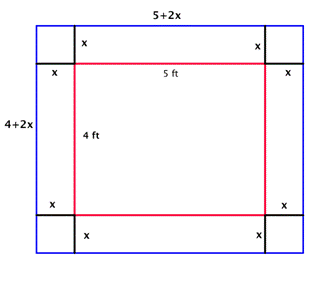
Since each side of the original 4 x 5 quilt has the border of width x added, the length of the quilt with the border will be 5 + 2x, and the width will be 4 + 2x.
(This is where you may start to think “Ah ha, this may be a quadratic equation after all. We have both dimensions written in the same variable, and will multiply them to get an area!") | |
| Area of border = Area of the blue rectangle minus the area of the red rectangle
Area of border = (4 + 2x)(5 + 2x) – (4)(5)
|
| We are only interested in the area of the border strips. Write an expression for the area of the border. | |
|
10 = (4 + 2x)(5 + 2x) – 20 |
| We have 10 sq ft of fabric for the border, so set the area of the border to be 10. | |
|
|
|
Multiply (4 + 2x)(5 + 2x). | |
|
|
|
Simplify. | |
|
|
| Subtract 10 from both sides so that we have a quadratic equation set equal to zero and can apply the quadratic formula to find the roots of the equation. | |
|
|
| Use the quadratic formula. In this case, a = 4, b = 18, and c = -10. | |
|
|
|
Simplify. | |
|
or
|
| Find the solutions, making sure that the ± is evaluated for both values.
Ignore the solution x = -5, as the width could not be negative.
| |
| Answer |
The width of the border should be 0.5 ft. |
|
|
| You are provided with the following price vs. quantity information. Write an equation that will represent yearly profit P for a selling price s. The production cost per item is $30.
A) P = -10s + 8000 B) P = sq – 30q C) P = D) P =
|
Summary
Quadratic functions are used in many types of real world situations. They are useful in describing the trajectory of a ball, determining the height of a thrown object and in optimizing profit for businesses. When solving a problem using a quadratic function it may be necessary to find the vertex or to describe a section of the parabola.