Solving Quadratic Equations Using the Quadratic Formula
Learning Objective(s)
· Solve quadratic equations using the quadratic formula.
Introduction
We can solve any quadratic equation by completing the square—turning a polynomial into a perfect square trinomial. If we complete the square on the generic equation ![]() and then solve for x, we find that
and then solve for x, we find that ![]() . This rather awkward looking equation is known as the quadratic formula.
. This rather awkward looking equation is known as the quadratic formula.
This formula is very helpful for solving quadratic equations that are difficult or impossible to factor, and using it can be faster than completing the square. The quadratic formula can be used to solve any quadratic equation of the form ![]() .
.
Deriving the Quadratic Formula
Let's complete the square on the general equation, ![]() , and see exactly how that produces the quadratic formula. Recall the process of completing the square:
, and see exactly how that produces the quadratic formula. Recall the process of completing the square:
· Start with an equation of the form ![]() .
.
· Rewrite the equation so that ![]() is isolated on one side.
is isolated on one side.
· Complete the square by adding ![]() to both sides.
to both sides.
· Rewrite as a square of a binomial and solve for x.
Can you complete the square on the general quadratic equation ![]() ? Try it yourself before you continue to the example below. Hint: When working with the general equation
? Try it yourself before you continue to the example below. Hint: When working with the general equation ![]() , there is an added complication, in that the coefficient of
, there is an added complication, in that the coefficient of ![]() is not equal to 1. You can divide the equation by a, which makes some of the expressions a bit messy, but if you are careful, everything will work out, and at the end, you’ll have the quadratic formula!
is not equal to 1. You can divide the equation by a, which makes some of the expressions a bit messy, but if you are careful, everything will work out, and at the end, you’ll have the quadratic formula!
| Example | |||||
| Problem | Complete the square of |
|
| ||
|
|
|
| Divide both sides of the equation by a, so that the coefficient of | ||
|
|
|
| Rewrite so the left side is in the form | ||
|
|
|
| Add | ||
|
|
|
| Write the left side as a binomial squared. | ||
|
|
|
| Evaluate | ||
|
|
|
| Write the fractions on the right side using a common denominator. | ||
|
|
|
| Add the fractions on the right. | ||
|
|
|
| Take the square root of both sides. Remember that you want both the positive and negative square roots! | ||
|
|
|
| Subtract | ||
|
|
|
| The denominator under the radical is a perfect square, so
| ||
|
|
|
| Add the fractions since they have a common denominator. | ||
| Answer |
|
|
| ||
There we have it, the quadratic formula.
The quadratic formula will work with any quadratic equation, but only if the equation is in standard form, ![]() . To use it, follow these steps:
. To use it, follow these steps:
· Put the equation in standard form first.
· Identify the coefficients, a, b, and c. Be careful to include negative signs if the bx or c terms are subtracted.
· Substitute the values for the coefficients into the quadratic formula.
· Simplify as much as possible.
· Use the ± in front of the radical to separate the solution into two values: one in which the square root is added, and one in which it is subtracted.
· Simplify both values to get the possible solutions.
That's a lot of steps. Let’s try them:
| Example | ||||
| Problem | Use the quadratic formula to solve the equation |
| ||
|
|
|
| a = 3, b = -11, c = -4
Note that the subtraction signs mean the coefficients b and c are negative. | |
|
|
|
| Substitute values into the quadratic formula. | |
|
|
|
| Simplify, being careful to get the signs correct. | |
|
|
|
| Simplify some more. | |
|
|
|
| Simplify the radical: | |
|
|
or
|
| Separate and simplify to find the solutions to the quadratic equation. Note that in one, 13 is added and in the other, 13 is subtracted. | |
| Answer | x = 4 or |
|
| |
The solution to the quadratic equation gives the x-coordinates of the x-intercepts, or the roots of a quadratic equation. The roots of the quadratic equation are the values where the parabola crosses the x-axis. We can check this by looking at the graph of the function ![]() and see that the roots are (4, 0) and (
and see that the roots are (4, 0) and (![]() , 0).
, 0).
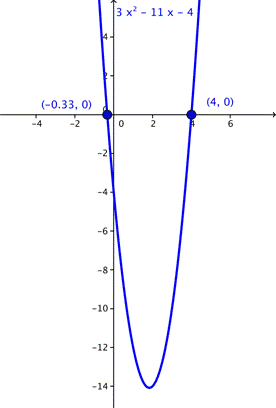
The example above shows a quadratic equation with two solutions. Below is an example with one solution. Compare the simplified radicals of the two examples:
| Example | |||||
| Problem | Use the quadratic formula to solve the equation |
|
| ||
|
|
|
| Subtract 6x from each side and add 16 to both sides to put the equation in the form |
| |
|
|
|
| Identify the coefficients a, b, and c. x2 = 1x2, so a = 1. Since 8x is subtracted, b is negative.
a = 1, b = -8, c = 16. |
| |
|
|
|
| Apply the quadratic formula. |
| |
|
|
|
| Simplify |
| |
|
|
|
| Since the square root of 0 is 0, and adding or subtracting 0 both give the same result, there is only one possible value. |
| |
| Answer | x = 4
|
|
|
| |
This quadratic equation has only one solution, so the graph of the function ![]() will touch the x-axis once. It has only one root.
will touch the x-axis once. It has only one root.
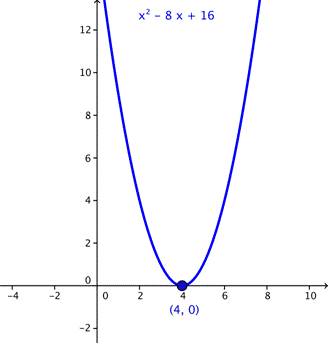
Something to notice—the quadratic equation ![]() can be factored to
can be factored to ![]() . So although the quadratic formula gave us the solution, it would have been faster to factor it. It's worth checking to see if a quadratic equation can be easily factored before applying the quadratic formula.
. So although the quadratic formula gave us the solution, it would have been faster to factor it. It's worth checking to see if a quadratic equation can be easily factored before applying the quadratic formula.
| Use the quadratic formula to solve the equation
A) x = 2 B) x =11, x = -9 C) D)
|
The Discriminant
A quadratic equation may have two roots, one root, or no roots. In the quadratic formula, the expression underneath the radical symbol determines how many solutions the formula will have. This expression, ![]() , is called the discriminant of the equation
, is called the discriminant of the equation ![]() .
.
Let’s think about how ![]() will affect the evaluation of
will affect the evaluation of ![]() , and how it helps to determine the solution set.
, and how it helps to determine the solution set.
· If ![]() , then the number underneath the radical will be a positive value. We can always find the square root of a positive number, so evaluating the quadratic formula will result in two solutions (one by adding the positive square root, and one by subtracting it).
, then the number underneath the radical will be a positive value. We can always find the square root of a positive number, so evaluating the quadratic formula will result in two solutions (one by adding the positive square root, and one by subtracting it).
· If ![]() , then we will be taking the square root of 0, and the “±” term drops out of the evaluation of the quadratic formula. (Adding zero and subtracting zero will both give the same result.) There will be one solution.
, then we will be taking the square root of 0, and the “±” term drops out of the evaluation of the quadratic formula. (Adding zero and subtracting zero will both give the same result.) There will be one solution.
· If ![]() , then the number underneath the radical will be a negative value. Since we cannot find the square root of a negative number (at least not using the real number system), we cannot evaluate the formula any further. There will be no solutions.
, then the number underneath the radical will be a negative value. Since we cannot find the square root of a negative number (at least not using the real number system), we cannot evaluate the formula any further. There will be no solutions.
| Example | ||||
| Problem | Use the discriminant to determine whether the quadratic equation |
| ||
|
|
|
| Evaluate
a = 1, b = -4, and c = 10. | |
|
|
|
| The result is a negative number. The discriminant is negative, so the quadratic equation has no solution. | |
| Answer |
no solution |
|
| |
| Suppose a quadratic equation has a discriminant that evaluates to zero. Which of the following statements is always true?
A) The equation has two solutions and the graph of the parabola will open upward. B) The equation has one solution and the graph of the parabola will open downward. C) The equation has one solution and you can’t tell anything about the direction of the parabola. D) The equation has zero solutions and you can’t tell anything about the direction of the parabola.
|
Summary
The quadratic formula, ![]() , is found by completing the square of the quadratic equation
, is found by completing the square of the quadratic equation ![]() . The formula can be used to find the solution to a quadratic equation and to identify any possible roots, or x-intercepts, of the function.
. The formula can be used to find the solution to a quadratic equation and to identify any possible roots, or x-intercepts, of the function.
The discriminant of the quadratic formula is the quantity under the radical, ![]() . It determines how many solutions there are to the quadratic equation. If the discriminant is positive, there are 2 roots. If it is zero, there is 1 root. If the discriminant is negative, there are 0 roots.
. It determines how many solutions there are to the quadratic equation. If the discriminant is positive, there are 2 roots. If it is zero, there is 1 root. If the discriminant is negative, there are 0 roots.
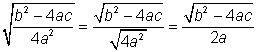 .
.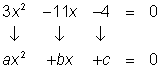
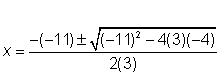
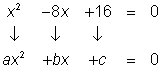
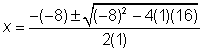
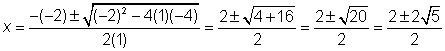 . The answer is
. The answer is 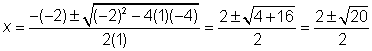 . If you ignore the square root, this becomes x = 11 or x = –9, so you may have forgotten to take the square root of 20.
. If you ignore the square root, this becomes x = 11 or x = –9, so you may have forgotten to take the square root of 20. 