Resolviendo Ecuaciones Cuadráticas Completando el Cuadrado

 

Objetivo de Aprendizaje

·         Resolver ecuaciones cuadráticas completando el cuadrado.

 

 

Hay veces que una [ecuación cuadrática] es imposible de factorizar. Para resolver ese tipo de ecuaciones cuadráticas, son necesarias otras estrategias. Completar el cuadrado es una de ellas. Convierte un polinomio en un trinomio cuadrado perfecto, el cual es más fácil de graficar y resolver.

 

 

"Completar el Cuadrado" consiste exactamente en eso — tomar algo que probablemente no es un cuadrado y convertirlo en uno. Podemos ilustrar esta idea usando el modelo de área de un binomio x² + bx:

 

 

En este ejemplo, el área de todo el rectángulo está dada por x(x + b). 

 

Ahora vamos a convertir este rectángulo en un cuadrado. Primero, dividimos el rectángulo rojo con área bx en dos rectángulos iguales cada uno con área . Luego rotamos y cambiamos de posición uno de ellos. No hemos cambiado el tamaño del área roja — sigue siendo bx.

 

 

 

 

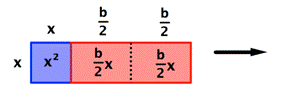
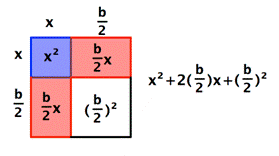
Los rectángulos rojos ahora forman dos lados de un cuadrado, mostrado en blanco. El área de ese cuadrado es la longitud de los rectángulos rojos elevada al cuadrado .

 

Aquí viene lo interesante — ¿puedes ver que cuando el cuadrado blando es sumado a las regiones azul y rojas, el área total también es un cuadrado? En otras palabras, ¡hemos "completado el cuadrado"! Al sumar la cantidad al binomio original, hemos creado un cuadrado, un cuadrado con lados :

 

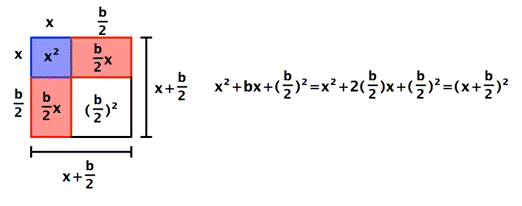
Nota que el área de este cuadrado puede ser escrita de dos maneras, como , y como .

 

 

Completando el Cuadrado   Para completar el cuadrado en una expresión de la forma x2 + bx, sumar . Y la expresión se vuelve .

 

 

Veamos un ejemplo usando números en lugar del modelo de área. Completaremos el cuadrado del binomio . Para hacer eso, necesitamos encontrar un valor de c tal que  sea un trinomio cuadrado perfecto.

 

 

Nuestro trinomio cuadrado perfecto es . También lo podemos escribir como el cuadrado de un binomio: . 

 

Nota que es siempre positivo, ya que es el cuadrado de un número. Cuando completamos el cuadrado, siempre estamos sumando un valor positivo.

 

Encuentra el valor de c que vuelve  un trinomio cuadrado perfecto usando la técnica de completar el cuadrado. Luego escribe la expresión como el cuadrado de un binomio.   A) c = 12; B) c = 36; C) c = -12; D) c = 36;   Mostrar/Ocultar la Respuesta A) Incorrecto. El valor de b es -12, entonces c es . La respuesta correcta es D.   B) Incorrecto. El valor de c ha sido calculado correctamente: . Sin embargo, el trinomio resultante es , que se factoriza como , no . La respuesta correcta es D.   C) Incorrecto. El valor de b es -12, entonces c es .  Nota también que c es igual al cuadrado de un número, por lo que siempre será positivo. La respuesta correcta es D   D) Correcto. El valor de c es y el trinomio resultante, se factoriza como .

 

 

 

Cuando resolvemos una ecuación cuadrática que ha sido igualada a cero, como  o , encontramos los valores de x que hacen que la ecuación sea válida. Cuando empezamos con una función cuadrática, como , encontramos las raíces de una ecuación cuadrática al igualar y a cero y resolver. Esto se llama "resolver la cuadrática." Las raíces de  están localizadas en la gráfica donde la parábola cruza o toca el eje x. También se les llama las intersecciones en x de la gráfica. Para ecuaciones cuadráticas que pueden ser factorizadas, como o , encontramos las raíces igualando la ecuación a cero y usando la Propiedad Cero de la Multiplicación para encontrar cualquier coordenada x posible.

 

Pero, ¿cómo encontramos las raíces de una ecuación cuadrática que no puede ser factorizada? Existen muchas ecuaciones cuadráticas que no pueden ser factorizadas y que de todas maneras tienen soluciones o raíces. Podemos usar la técnica de completar el cuadrado para resolver estas ecuaciones cuadráticas. Aquí hay un ejemplo:

 

 

Recuerda que cuando sacamos las raíces cuadradas de ambos lados de la ecuación, la respuesta es el valor positivo y el negativo de la raíz cuadrada. Los matemáticos usan un símbolo especial para esto: ±, que se lee como "más menos". Usando este símbolo, el par de ecuaciones anteriores,  y , se pueden escribir como una ecuación: .

 

El ejemplo anterior muestra una ecuación cuadrática que tiene un coeficiente de 1 en el término cuadrático. Podemos trabajar de la misma manera si el coeficiente es un número distinto de 1, pero debemos recordar dividir ambos lados de la ecuación por este coeficiente antes de completar el cuadrado.

 

 

En los dos problemas que hemos resuelto, cada ecuación cuadrática tuvo dos soluciones, lo que significa que la ecuación representa una parábola con dos raíces. Piensa por un momento sobre el caso de 1 raíz o solución. En ese caso, la gráfica de la cuadrática tocará el eje x sólo en un lugar y la solución tendrá sólo un valor para la coordenada x.

 

¿Y qué pasa con las parábolas que nunca tocan el eje x? En esos casos, nos toparemos con la necesidad de sacar la raíz cuadrada de un número negativo cuando resolvemos la ecuación. No puedes calcular la raíz cuadrada de un número negativo, lo que significa que no existe raíz.

 

Las ecuaciones cuadráticas también pueden tener sólo una solución. Aquí hay un ejemplo:

 

 

También pudimos haber resuelto la ecuación notando que el trinomio ya era un cuadrado perfecto y reescribiéndolos directamente como un binomio cuadrado.

 

Completar el cuadrado es una herramienta útil cuando convertimos una ecuación cuadrática que está en la forma estándar de una ecuación cuadrática () a una que está en la forma vértice de una ecuación cuadrática, o . En la forma vértice, el punto (h, k) será el vértice, el cual es el punto más bajo de una parábola (si el valor de a es positivo y la parábola se abra hacia arriba) o el punto más alto (si el valor de a es negativo y la parábola se abre hacia abajo).

 

Aquí hay un ejemplo donde usamos la técnica de completar el cuadrado para convertir una ecuación cuadrática de su forma estándar a su forma vértice

 

 

 

Nota que el valor del coeficiente a es el mismo en ambas formas vértice y estándar. Podemos usar esto para explicar por qué el punto (h, k) es el vértice de la parábola cuando su ecuación se escribe como . Existen dos casos:

 

1)      El valor de a es positivo: Entonces, el valor más pequeño que  puede tener es 0, cuando h es igual a x. En este caso, y = k. Para cualquier valor diferente de x,  es mayor que 0, entonces y debe ser mayor que k porque un valor positivo es añadido a k para obtener y. Por lo tanto, el valor más pequeño de y es igual a k, y el punto más bajo de la parábola es (h, k).

 

2)      El valor de a es negativo: Se aplica el mismo razonamiento, excepto que esta vez  es una cantidad negativa debido a que el valor de a es negativo y (x – h)² siendo positivo y las dos cantidades siendo multiplicadas crean una cantidad negativa. Por lo que la cantidad  ≤ 0, y toma en su valor más grande de cero cuando x = h. Por lo tanto, el punto más alto de la parábola es (h, k).

 

Usar la técnica de completar el cuadrado para escribir la ecuación cuadrática n en su forma vértice e identificar el vértice.   A) ; (1, -10) B) ; (-1,-10) C) ; (3, -2) D) ; (-1, 10)   Mostrar/Ocultar la Respuesta A) Correcto. El trinomio cuadrado perfecto  se factoriza como , por lo que la ecuación se transforma en  y el vértice es correctamente identificado como (1, -10).   B) Incorrecto. El trinomio cuadrado perfecto se factoriza como  no . La respuesta correcta es ; (1, -10).   C) Incorrecto. Es incorrecta la forma en que completaste el cuadrado (aunque el vértice identificado (3, -2) sí corresponde con la ecuación incorrecta que encontraste). La respuesta correcta es ; (1, -10).  D) Incorrecto. La ecuación está escrita correctamente, pero el vértice que identificaste es el incorrecto. (1, -10) es el vértice. La respuesta correcta es ; (1, -10)..

 

 

La técnica de completar el cuadrado es usada para cambiar un binomio de la forma  a un trinomio cuadrado perfecto , el cual puede ser factorizado como .  Cuando resolvemos ecuaciones cuadráticas, completar el cuadrado es útil para encontrar las raíces de la ecuación cuadrática, pero debemos ser cuidadosos de sumar  a ambos lados de la ecuación para mantener la igualdad.

 

Completar el cuadrado también nos ayuda a convertir una ecuación cuadrática a su forma vértice, y = a(x – h)² + k. En la forma vértice de una ecuación cuadrática, las coordenadas del vértice están dadas por (h, k).