Solving Quadratic Equations by Completing the Square

 

Learning Objective(s)

·         Solve quadratic equations by completing the square.

 

 

Sometimes a [quadratic equation] is impossible to factor. To solve this kind of quadratic equation, different strategies are needed. Completing the square is such a strategy. It turns a polynomial into a perfect square trinomial, which is easier to graph and to solve.

 

 

“Completing the Square” does exactly what it says—it takes something that probably is not a square and makes it one. We can illustrate this idea using an area model of the binomial x² + bx:

 

 

In this example, the area of the overall rectangle is given by x(x + b). 

 

Now let's make this rectangle into a square. First, we'll divide the red rectangle with area bx into two equal rectangles each with area . Then we'll rotate and reposition one of them. We haven't changed the size of the red area—it still adds up to bx.

 

 

 

 

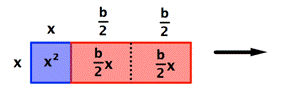
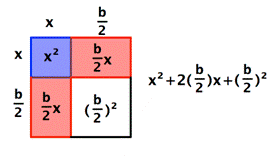
The red rectangles now make up two sides of a square, shown in white. The area of that square is the length of the red rectangles squared, or .

 

Here comes the cool part—do you see that when the white square is added to the blue and red regions, the whole shape is now a square too? In other words, we've "completed the square!" By adding the quantity to the original binomial, we've made a square, a square with sides of :

 

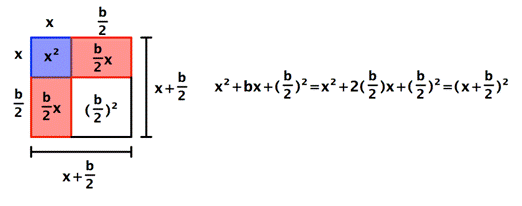
Notice that the area of this square can be written in two ways, as , and as .

 

 

Completing the Square   To complete the square on an expression of the form x2 + bx, add . Then the expression becomes .

 

 

Let’s look at an example using numbers instead of an area model. We'll complete the square for the binomial . To do that, we need to find a value c so  becomes a perfect square trinomial.

 

 

Our perfect square trinomial is . We can also write that as the square of a binomial: . 

 

Notice that is always positive, since it is the square of a number. When we complete the square, we are always adding a positive value.

 

Use completing the square to find the value of c that makes  a perfect square trinomial. Then write the expression as the square of a binomial.   A) c = 12; B) c = 36; C) c = -12; D) c = 36;   Show/Hide Answer A) Incorrect. The value of b is -12, so c is . The correct answer is D.   B) Incorrect. The value of c is calculated correctly: . However, the resulting trinomial is , which factors to , not . The correct answer is D.   C) Incorrect. The value of b is -12, so c is .  Note also, that because c is equal to the square of a number, it will always be positive. The correct answer is D.   D) Correct. The value of c is  and the resulting trinomial  factors to .

 

 

 

When we solve a quadratic equation that has been set equal to zero, such as  or , we find the value(s) of x that makes the equation true. When we start with a quadratic function, such as , we find the roots of a quadratic equation by setting the y equal to zero and solving.  This can be called “solving the quadratic.” The roots of  are located on the graph where the parabola crosses or touches the x-axis. They are also called the x-intercepts of the graph. For quadratic equations that can be factored, such as or , we find the roots by setting the equation equal to zero and using the zero property to find any possible x-coordinates.

 

But how would we find the roots for a quadratic equation that cannot be factored? There are many non-factorable quadratic equations that still have solutions or roots. We can use completing the square to help us solve a quadratic equation that cannot be solved by factoring. Here is an example:

 

 

Remember that when we take square roots of both sides of an equation, the answer is both the positive and negative value of the square root. Mathematicians use a special symbol for this: ±, which is read as "plus or minus." Using this symbol, the pair of equations above,  and , could be written as one equation: .

 

The above example showed a quadratic equation that has a coefficient of 1 on the squared term. We can work the same way if the coefficient is a number other than one, but we must remember to divide both sides of the equation by this coefficient before completing the square.

 

 

In both of the problems we just solved, each quadratic equation had two solutions, which means the equation represents a parabola with two roots. Think for a moment about the case of 1 root or solution. In that case, the graph of the quadratic will touch the x-axis in one place and the solution will have only one x-coordinate value.

 

What about parabolas that never meet the x-axis? In those cases, we will find ourselves needing to take the square root of a negative number as we solve the equation. You cannot take the square root of a negative number, which is the tip-off that there is no root.

 

Quadratic equations can also have just one solution. Here is an example:

 

 

We also could have solved the equation by noticing that the trinomial was already a perfect square and going straight to rewriting it as a binomial squared.

 

Completing the square is also a useful tool when converting a quadratic equation that is in the standard form of a quadratic equation () to one that is in the vertex form of a quadratic equation, or .  In vertex form, the point (h, k) will be the vertex, which is either the lowest point of the parabola (if a is positive and the parabola opens upward) or the highest point (if a is negative and the parabola opens downward).

 

Here is an example where we use completing the square to convert a quadratic equation in standard form to vertex form:

 

 

 

Notice that the value of the coefficient a is the same in both vertex and standard form. We can use this to help explain why the point (h, k) is the vertex of the parabola when its equation is written as . There are two cases:

 

1)      The value of a is positive: Then, the smallest value  can have is zero, when h is equal to x. In that case, y = k. For any other value of x,  is greater than 0, so y must be greater than k because a positive value is added to k to get y. Therefore, the smallest value of y is equal to k, and the lowest point of the parabola is (h, k).

 

2)      The value of a is negative: The same reasoning applies, except that this time  is a negative quantity due to a being negative and (x – h)² being positive and the two quantities being multiplied creating a negative quantity. Thus the quantity  ≤ 0, and it takes on its largest value of zero when x = h. Therefore, the highest point of the parabola is (h, k).

 

Use completing the square to write the quadratic equation  in vertex form and then identify the vertex.   A) ; (1, -10) B) ; (-1,-10) C) ; (3, -2) D) ; (-1, 10)   Show/Hide Answer A) Correct. The perfect square trinomial  factors to , so the equation transforms to  and the vertex is correctly identified as (1, -10).   B) Incorrect. The perfect square trinomial  factors to  not . The correct answer is ; (1, -10).   C) Incorrect. Completing the square was done incorrectly (although the identified vertex of (3, -2) does correspond with the incorrect equation you found). The correct answer is ; (1, -10).   D). Incorrect. The equation is written correctly, however the vertex is identified incorrectly. (1, -10) is the vertex. The correct answer is ; (1, -10).

 

 

Completing the square is used to change a binomial of the form  to a perfect square trinomial , which can be factored to .  When solving quadratic equations, completing the square is used to find the roots of the quadratic equation, but we must be careful to add  to both sides of the equation to maintain equality.

 

Completing the square also helps us convert a quadratic equation into vertex form, y = a(x – h)² + k. In the vertex form of a quadratic equation, the coordinates of the vertex are given by (h, k).