Factorizando Trinomios por Agrupación 1

 

Objetivo de Aprendizaje

·         Factorizar polinomios de la forma x² + bx + c usando la técnica de agrupación.

 

 

Un polinomio con tres términos se llama trinomio. Los trinomios normalmente (¡pero no siempre!) tienen la forma x² + bx + c. A primera vista, podría parecer difícil factorizar trinomios y polinomios con un número impar de términos, pero una técnica llamada agrupación nos da la solución. Agrupar es una estrategia de divide y vencerás — nos permite factorizar polinomios grandes en pares de términos, en lugar de uno por uno.

 

Empecemos por considerar cómo el uso de la técnica de agrupación con polinomios de 4 términos. Luego aplicaremos este método a los casos especiales de trinomios de la forma x² + bx + c.

 

 

Cuando factorizamos el polinomio de dos términos 12r² – 8r como 4r(3r – 2), usamos la Propiedad Distributiva, la cual establece que a(b + c) = ab + ac. Sacamos el máximo factor común (MFC) de dos monomios (a), sumamos los factores detrás (b + c), y reescribimos la expresión como el producto de dos (esto nos da a(b + c)).

 

Podemos aplicar la misma técnica para factorizar polinomios de tres o más términos: donde sea que encontramos factores comunes entre los monomios, los sacamos y reescribimos la expresión.

 

Este proceso es más fácil cuando usamos la técnica de agrupación. Lo hacemos así:

• Agrupar en pares los términos del polinomio
• Factorizar cada par de términos (encontrar el máximo factor común y luego usar la Propiedad Distributiva para sacar el MFC)
• Buscar factores comunes entre formas factorizadas de los términos en pares
• Factorizar el polinomio común a partir de los grupos

 

Veamos cómo aplicar la técnica de agrupación para factorizar un polinomio de 4 términos

 

 

Detengámonos aquí para ver cómo ha cambiado el polinomio original. La Propiedad Distributiva ha sido aplicada dos veces, creando dos términos que son cada uno el producto de un monomio por un binomio: 4a(b + 3) y 3(b + 3). ¡Bien! Pero, ¿ahora qué?

 

Nota que los nuevos términos tienen un factor común: (b + 3). Seguramente podemos aprovechar eso.

 

Piensa cómo factorizaríamos 4ax + 3x. ¿Qué factores comparten 4ax y 3x ? El máximo factor común es x, por lo que sacaríamos ese factor y reescribiríamos el polinomio como x(4a + 3). ¿Tiene sentido? Bueno, nuestro polinomio, 4a(b + 3) + 3(b + 3), se parece pero con (b + 3) en lugar de x. Por lo que podemos factorizarlo de la misma manera, sacando (b + 3) igual que como sacamos x:

 

 

 

Nota que cuando factorizamos dos términos, el resultado es un monomio multiplicado por un polinomio, Pero la forma factorizada de un polinomio de cuatro términos es el producto de dos polinomios.

 

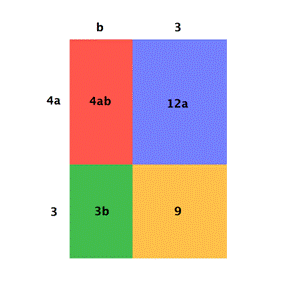
Abajo hay una representación visual de lo que acabamos de hacer. Nota cómo los términos individuales en los factores se multiplican para crear los cuatro términos del polinomio original. El rectángulo completo tiene dimensiones (b + 3) y (4a + 3). Los cuatro rectángulos más pequeños que conforman su área son cada término diferente en el polinomio original. La forma factorizada y la forma original del polinomio son equivalentes.

 

 

Factorizar: 10ab + 5b + 8a +4   A) (2a + 1)(5b + 4)   B) (5b + 2a)(4 + 1)   C) 5(2ab + b + 8a + 4)   D) (4 + 2a)(5b + 1)   Mostrar/Ocultar la Respuesta A) Correcto. Considera la siguiente solución: 10ab + 5b + 8a +4 (10ab + 5b) + (8a +4) 5b(2a + 1) + 4(2a + 1) (2a + 1)(5b + 4)   B) Incorrecto. Cuando factorizamos 5b a partir de 10ab y 5b, los términos 2a y 1 que sobran deben ser sumados y multiplicados por el factor común 5b: 5b(2a + 1). De manera similar, factorizar el 4 de 8a + 4 nos deja 4(2a + 1). Entonces puedes factorizar (2a + 1) de la suma de ambas expresiones para obtener la factorización correcta, (2a + 1)(5b + 4).   C) Incorrecto. El 5 es factor común solamente de 10ab + 5b, lo que nos da 5b(2a + 1). El otro par, 8a + 4, tiene un factor común de 4. Factorizarlos nos da 4(2a + 1). Ya que ambas expresiones tienen el factor común 2a + 1, puedes factorizar de nuevo para obtener (2a + 1)(5b + 4).   D) Incorrecto. Identificaste correctamente 5b como factor común de un par, dejando 2a y 1, y 4 como el factor del otro par, también dejando 2a y 1. Sin embargo, esto nos da 5b(2a + 1) + 4(2a + 1). Si tuvieras 5bx + 4x, podrías factorizar la x para obtener x(5b + 4), entonces factorizar el (2a + 1) nos da (2a + 1)(5b + 4).

 

Intentemos factorizar otro polinomio de 4 términos. Nota que en el ejemplo siguiente, el primer término es x², y x es la única variable presente — los otros ejemplos que has visto hasta ahora han incluido dos variables, pero sin términos al cuadrado.

 

 

Nota que ambos factores, (x + 2) y (x + 5), contienen el término x. Así es como normalmente se factorizan los términos al cuadrado, y esto nos lleva al siguiente tema: factorizando trinomios.

 

 

Los polinomios con tres términos se llaman trinomios, Algunos trinomios tienen la forma x² + bx + c. Los trinomios pueden ser factorizados de la misma manera que otros polinomios, una vez más, la idea clave es la agrupación.

 

Empecemos con el trinomio x² + 7x + 10. A primera vista, parece que este trinomio no puede ser factorizado, porque los términos individuales x², 7x, y 10 no tienen factores comunes. Podríamos sacar la x de los primeros dos términos, pero eso nos dejaría x(x + 7) + 10, que no parece muy útil.

 

Pero mira más de cerca…x² + 7x + 10 se parece mucho al polinomio x² + 2x + 5x + 10 que acabamos de resolver, De hecho, si sumas 2x y 5x, obtienes 7x, ¡entonces los polinomios son equivalentes! Y si pudimos factorizar x² + 2x + 5x + 10 (recuerda, llegamos a (x + 2)(x + 5)) entonces también podemos factorizar x² + 7x + 10. Entonces, ¿cómo lo hacemos?

 

Pensar en x² + 7x + 10 como x² + 2x + 5x + 10 nos ayuda bastante para factorizar el trinomio, porque ahora podemos usar grupos y la Propiedad Distributiva para sacar los factores comunes. Esta es una estrategia para factorizar trinomios de la forma x² + bx + c: expandir el término bx como una suma de dos cantidades.

 

¡Perfecto! Pero espera, ¿Cómo sabemos qué números usar para separar bx? Por suerte, existe una regla para ello:

 

Factorizando Trinomios   Para factorizar un trinomio de la forma x2 + bx + c, encontrar dos enteros, r y s, tales que su suma es b y su producto es c. Reescribir el trinomio como x2 + rx + sx + c y luego usar agrupación y la Propiedad Distributiva para factorizar el polinomio. Los factores resultantes serán (x + r) y (x + s).

 

Una forma de entender por qué este método funciona es observar qué pasa cuando la expresión (x + r)(x + s) es evaluada: se convierte en x² + rx + sx + rs, como se muestra en el diagrama de abajo. El cuadro azul es x², el cual se encuentra en ambas formas del polinomio. El rectángulo rojo representa rs en la forma expandida, la versión de 4 términos del polinomio y c en el trinomio original. Los dos rectángulos verdes son rx + sx en la forma expandida y bx en la expresión original.

 

 

 

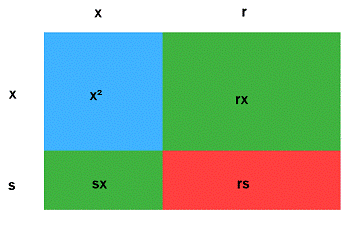
En otras palabras, hemos tomado las tres partes del trinomio (representado por los tres colores en el diagrama), y las hemos dividido en dos (mostrado como los 4 rectángulos). El tamaño de las piezas ha cambiado, pero el valor total es el mismo.

 

Cuando usamos este método de factorización de trinomios, estamos buscando una forma de convertir los tres términos en 4 términos

 

Usemos este método para factorizar el trinomio a² + a – 12. En este trinomio, el término bx es a o 1a y el término c es -12. (Es importante notar que este término es -12, y no +12. ¡Esto importará cuando busquemos los pares multiplicativos!)  Queremos encontrar los dos enteros, r y s, tales que su suma sea 1 y su producto sea -12.

 

Una tabla nos puede ayudar a organizar las posibilidades, A la izquierda enlistaremos todos los posibles factores de -12; a la derecha sumaremos los término r y s. ¿Qué valores de r y s cumplen nuestros criterios?

 

 

Sólo existe una combinación donde r • s = -12 y r + s = 1: cuando r = 4, y s = -3. Usémoslos para factorizar el trinomio original.

 

 

 

Factorizar trinomios es cuestión de práctica y paciencia. ¡Algunas veces el número de combinaciones apropiado será simplemente obvio! Otras veces, a pesar de tratar muchas posibilidades, las combinaciones correctas son difíciles de encontrar.

 

Mientras que no existe una forma infalible de encontrar la combinación correcta al primer intento, existen algunos consejos que pueden facilitar el trabajo. Piensa en el por qué cada uno de estos consejos es válido:

 

Consejos para Encontrar Valores que Funcionarán   Cuando se factoriza un trinomio de la forma x2 + bx + c, se pueden seguir los siguientes consejos:   Considerar primero el término c. ·         Si el término c es un número positivo, entonces los factores de c serán ambos positivos o negativos. En otras palabras, r y s tendrán el mismo signo. ·         Si el término c es un número negativo, entonces un factor de c será positivo , y el otro factor de c será negativo. Alguno de r o s será negativo, pero no ambos.   Después considerar el término b. ·         Si el término c es positivo y el término b es positivo, entonces r y s son > 0. ·         Si el término c es positivo y el término b es negativo, entonces r y s son < 0. ·         Si el término c es negativo y el término b es positivo, entonces el factor positivo tendrá un valor absoluto más grande. Esto es, si |r| > |s|, entonces r es positivo y s es negativo. ·         Si el término c es negativo y el término b es negativo, entonces el factor negativo tendrá un valor absoluto más grande. Esto es, si |r| > |s|, entonces r es negativo y s es positivo.

 

 

Jess está tratando de usar el método de agrupación para factorizar el trinomio v2 – 10v + 21. ¿Cómo debería reescribir el término central b, -10v?   A) +7v + 3v   B) -7v – 3v   C) -7v + 3v   D) +7v – 3v   Mostrar/Ocultar la Respuesta A) Incorrecto. Como el término c es positivo y el término b es negativo, ambos términos deberían ser negativos. (Nota que usando los enteros 7 y 3, 7 + 3 = + 10, por lo que tendríamos el término 10v en lugar de -10v.) La respuesta correcta es -7v – 3v.   B) Correcto. Como el término c es positivo y el término b es negativo, ambos términos deberían ser negativos. Comprobación: Al usar los enteros -7 y -3, -7 + -3 = -10 y -7 • -3 = 21, tenemos que los términos resultantes -10v y 21 son correctos.   C) Incorrecto. Como el término c es positivo y el término b es negativo, ambos términos deberían ser negativos. (Nota que usando los enteros -7 y 3, -7 + 3 = -4 y -7 • 3 = -21, por lo que tendríamos el término -4v en lugar de -10v y -21 en lugar de 21.) La respuesta correcta es -7v – 3v.   D) Incorrecto. Como el término c es positivo y el término b es negativo, ambos términos deberían ser negativos. (Nota que usando los enteros 7 y -3, 7 + -3 = 4 y 7 • -3 = -21, por lo que tendríamos el término 4v en lugar de -10v y -21 en lugar de 21.) La respuesta correcta es -7v – 3v.

 

 

 

Cuando usamos agrupación para factorizar un polinomio de cuatro términos, encontramos el factor común de pares de términos en lugar del de todo el polinomio. Usamos la Propiedad Distributiva para reescribir los términos agrupados como el factor común multiplicado por un binomio. Finalmente, sacamos cualquier binomio común de los grupos factorizados. El polinomio factorizado completamente será el producto de dos binomios.

 

Para factorizar trinomios de la forma x² + bx + c, encuentra dos enteros, r y s, tales que su suma sea b y su producto sea c. Reescribe el trinomio como x² + rx + sx + c y luego usa agrupación y la Propiedad Distributiva para factorizar el polinomio.