Factoring Trinomials by Grouping 1

 

Learning Objective(s)

·         Factor polynomials of the form x² + bx + c by grouping.

 

 

A polynomial with three terms is called a trinomial. Trinomials often (but not always!) have the form x² + bx + c. At first glance, it may seem difficult to factor trinomials and polynomials with even more terms, but a technique called grouping has the answer. Grouping is a divide and conquer strategy—it lets us factor big polynomials a pair of terms at a time instead of all at once.

 

Let’s start by considering how to use the grouping technique with 4 term polynomials. Then we will apply this method to the special cases of trinomials in the form x² + bx + c.

 

 

When we factor the two-term polynomial 12r² – 8r as 4r(3r – 2), we are using the Distributive Property, which states that a(b + c) = ab + ac. We pull out the greatest common factor of two monomials (the a), add the factors left behind (the b + c), and rewrite the expression as the product of the two (that gives us a(b + c)).

 

We can apply this same technique to factoring polynomials of three or more terms: wherever we find common factors among monomials, we pull them out and rewrite the expression.

 

This process is easier when we use the grouping technique. Here's how we do it:

• Group the terms of the polynomial into pairs
• Factor each pair of terms (find their greatest common factor and then use the distributive property to pull out the GCF)
• Look for common factors between the factored forms of the paired terms
• Factor the common polynomial out of the groups

 

Let's see how that looks in action, when we use the grouping technique to factor a four-term polynomial.

 

 

Let’s stop here to take a look at how the original polynomial has changed. The Distributive Property has been applied twice, creating two terms that are each a product of a monomial and a binomial: 4a(b + 3) and 3(b + 3). Swell! But now what?

 

Notice that the new terms have a common factor: (b + 3). Surely we can make use of that.

 

Think about how we'd factor 4ax + 3x. What factors do 4ax and 3x share? The greatest common factor is x, so we'd pull that factor out and rewrite the polynomial as x(4a + 3). Make sense? Well our polynomial, 4a(b + 3) + 3(b + 3), is just like that except with (b + 3) instead of x. So we can factor it the same way, pulling out (b + 3) just like we pulled out x:

 

 

 

Notice that when we factor 2 terms, the result is a monomial times a polynomial. But the factored form of a 4-term polynomial is the product of 2 polynomials.

 

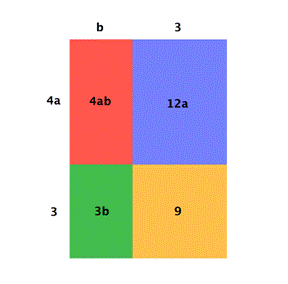
Below is a visual representation of what we just did. Notice how the individual terms in the factors multiply to create the 4 terms of the original polynomial. The entire rectangle has dimensions of (b + 3) and (4a + 3). The four smaller rectangles that make up its area are each a different term in the original polynomial. The factored form and the original form of the polynomial are equivalent.

 

 

Factor: 10ab + 5b + 8a +4   A) (2a + 1)(5b + 4)   B) (5b + 2a)(4 + 1)   C) 5(2ab + b + 8a + 4)   D) (4 + 2a)(5b + 1)   Show/Hide Answer A) Correct. Consider the following solution: 10ab + 5b + 8a +4 (10ab + 5b) + (8a +4) 5b(2a + 1) + 4(2a + 1) (2a + 1)(5b + 4)   B) Incorrect. When factoring 5b out of 10ab and 5b, the remaining 2a and 1 must still be added and multiplied by the common factor 5b: 5b(2a + 1). Similarly, factoring out the 4 from 8a + 4 leaves 4(2a + 1). Then you can factor (2a + 1) from the sum of those expressions to get the correct factorization, (2a + 1)(5b + 4).   C) Incorrect. The 5 is a common factor only for 10ab + 5b, giving 5b(2a + 1). The other pair, 8a + 4, have a common factor of 4. Factoring them gives 4(2a + 1). Since both expressions have a common factor of 2a + 1, you can factor again to give (2a + 1)(5b + 4).   D) Incorrect. You correctly identified 5b as a factor of one pair, leaving 2a and 1, and 4 as the factor of the other pair, also leaving 2a and 1. However, this gives 5b(2a + 1) + 4(2a + 1). If you had 5bx + 4x, you could factor out the x to get x(5b + 4), so factoring out the (2a + 1) gives (2a + 1)(5b + 4).

 

Let’s try factoring one more four-term polynomial. Notice that in the example below, the first term is x², and x is the only variable present—the other examples you have looked at so far have included two variables, but no squared terms.

 

 

Notice that both factors here, (x + 2) and (x + 5), contain the term x. This is often how squared terms are factored, and it leads us nicely into the next topic: factoring trinomials.

 

 

Polynomials with three terms are called trinomials. Some trinomials are in the form x² + bx + c. Trinomials can be factored just like other polynomials, and once again, the key is to use the idea of grouping that we just explored.

 

Let’s start with the trinomial x² + 7x + 10. At first glance, it looks like this trinomial cannot be factored, because the individual terms x², 7x, and 10 share no common factors. We could pull x out of the first two terms, but that would leave us with x(x + 7) + 10, which hardly seems helpful.

 

But let’s look closer…x² + 7x + 10 looks an awful lot like the polynomial x² + 2x + 5x + 10 that we just solved. In fact, if you add 2x and 5x, you get 7x, so the two polynomials are equivalent! And if we factored x² + 2x + 5x + 10 successfully (remember, we arrived at (x + 2)(x + 5)) then we should be able to factor x² + 7x + 10 as well. So how do we do it?

 

Thinking about x² + 7x + 10 as x² + 2x + 5x + 10 actually helps us factor the trinomial, because now we can use groups and the Distributive Property to pull out common factors. This is one strategy for factoring trinomials in the form x² + bx + c: expanding the term bx into the sum of two quantities.

 

Great! But wait. How do we know what numbers to break bx into? Lucky for us, there's a rule for that:

 

Factoring Trinomials   To factor a trinomial in the form x2 + bx + c, find two integers, r and s, whose sum is b and whose product is c. Rewrite the trinomial as x2 + rx + sx + c and then use grouping and the Distributive Property to factor the polynomial. The resulting factors will be (x + r) and (x + s).

 

One way to understand why this method works is to see what happens when the expression (x + r)(x + s) is evaluated: it becomes x² + rx + sx + rs, as shown in the diagram below. The blue square is x², which is present in both forms of the polynomial.  The red rectangle represents rs in the expanded, 4-term version of the polynomial and c in the original trinomial. The two green rectangles stand for rx + sx in the expanded form and bx in the original expression.

 

 

 

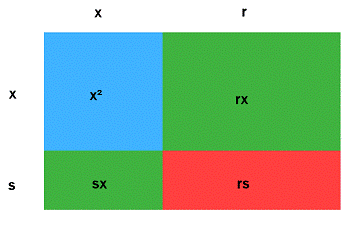
In other words, we've taken the three parts of the trinomial (represented by the three colors of the diagram), and split one of them in two (as shown by the 4 boxes). The size of the pieces has changed, but the total value is the same.

 

When we are using this method of factoring trinomials, we are looking for the way to turn three terms into four terms.

 

Let’s put this method to use and factor the trinomial a² + a – 12. In this trinomial, the bx term is a or 1a and the c term is -12. (It is important to note that this term is -12, not +12. This will matter when we find multiplicative pairs!)  We want to find two integers, r and s, whose sum is 1 and whose product is -12.

 

A chart will help us organize possibilities. On the left we'll list all possible factors of -12; on the right we'll add the r and s terms together. Which values for r and s meet our criteria?

 

 

There is only one combination where r • s = -12 and r + s = 1: when r = 4, and s = -3. Let’s use these to factor our original trinomial.

 

 

 

Factoring trinomials is a matter of practice and patience. Sometimes the appropriate number combinations will just pop out and seem so obvious! Other times, despite trying many possibilities, the correct combinations are hard to find.

 

While there is no foolproof way to find the right combination on the first guess, there are some tips that can ease the way. Think about why each of these tips is true:

 

Tips for Finding Values that Work   When factoring a trinomial in the form x2 + bx + c, consider the following tips:   Look at the c term first. ·         If the c term is a positive number, then the factors of c will both be positive or both be negative. In other words, r and s will have the same sign. ·         If the c term is a negative number, then one factor of c will be positive, and one factor of c will be negative. Either r or s will be negative, but not both.   Look at the b term second. ·         If the c term is positive and the b term is positive, then both r and s are > 0. ·         If the c term is positive and the b term is negative, then both r and s are < 0. ·         If the c term is negative and the b term is positive, then the positive factor will have the greater absolute value. That is, if |r| > |s|, then r is positive and s is negative. ·         If the c term is negative and the b term is negative, then the negative factor will have the greater absolute value. That is, if |r| > |s|, then r is negative and s is positive.

 

 

Jess is trying to use the grouping method to factor the trinomial v2 – 10v + 21. How should she rewrite the central b term, -10v?   A) +7v + 3v   B) -7v – 3v   C) -7v + 3v   D) +7v – 3v   Show/Hide Answer A) Incorrect. Because the c term is positive and the b term is negative, both terms should be negative. (Notice that using the integers 7 and 3, 7 + 3 = + 10, so this would provide the term 10v instead of -10v.) The correct answer is -7v – 3v.   B) Correct. Because the c term is positive and the b term is negative, both terms should be negative. Check: using the integers -7 and -3, -7 + -3 = -10 and -7 • -3 = 21, so this provides both terms -10v and 21 correctly.   C) Incorrect. Because the c term is positive and the b term is negative, both terms should be negative. (Notice that using the integers -7 and 3, -7 + 3 = -4 and -7 • 3 = -21, so this would provide -4v instead of -10v and -21 instead of 21.) The correct answer is -7v – 3v.   D) Incorrect. Because the c term is positive and the b term is negative, both terms should be negative. (Notice that using the integers 7 and -3, 7 + -3 = 4 and 7 • -3 = -21, so this would provide 4v instead of -10v and -21 instead of 21.) The correct answer is -7v – 3v.

 

 

 

When factoring a four-term polynomial using grouping, find the common factor of pairs of terms rather than the whole polynomial. Use the Distributive Property to rewrite the grouped terms as the common factor times a binomial. Finally, pull any common binomials out of the factored groups. The fully factored polynomial will be the product of two binomials.

 

To factor trinomials in the form x² + bx + c, find two integers, r and s, whose sum is b and whose product is c. Rewrite the trinomial as x² + rx + sx + c and then use grouping and the Distributive Property to factor the polynomial.