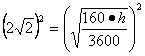Applying Radical Equations

 

Learning Objective(s)

·         Use radical equations to solve real world problems.

 

 

Mathematical problems that include radical equations arise in a number of professions, from engineering to nursing. Let’s take a look at some of the contexts within which radical equations arise and consider how to solve them.

 

 

Distance and size calculations using the Pythagorean Theorem often produce radicals because the formula contains three squared terms: a², b², and c². Consider the following problem:

 

A rectangular microchip has a length of 5 mm and a diagonal of  mm. What is the area of the microchip?

 

Before creating an equation for this problem, it makes sense to sketch a quick diagram. We are told that the microchip is rectangular, and we are also given the values for one length and the diagonal. We can assign any variable to represent the length of the side that we do not know—we’ll choose b.

 

 

 

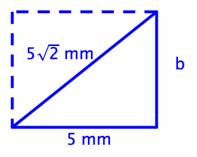
The dotted lines in the sketch above denote the edges of the microchip—it makes it easier to see the triangle that is created by the diagonal, length, and width.

 

Note that the problem asks for the area of the microchip. In order to find this, we will have to multiply the length (which we know to be 5 mm) and width (the length currently represented by the variable b).

 

Let’s use the Pythagorean Theorem to find the value for b.

 

 

We find that b has a value of 5. That means that the area of the microchip is 5 mm • 5 mm, or 25 mm².

 

 

Have you ever wondered how far you can see on a clear day? When we stand on the ground, environmental and man-made objects often block the view all the way to the horizon. But the higher we get—for instance, looking out the upper window of a tall building, or sitting at the top of a Ferris wheel—the further away we can see.

 

One estimate for how far we can see on a clear day is given by the formula , where v = visibility (in miles) and a = altitude (in feet).

 

A woman on a hang glider can see 49 miles to the horizon. Using the visibility formula, how far above the ground is she?

 

To solve this problem, let’s substitute our known values into the visibility formula. We will be left with a one-variable radical equation

 

 

The answer is 1600 feet! She is pretty high up in the air, but this makes sense, because she can see very far. To check our answer we should substitute 1600 back into our original equation and see if we get a true statement.

 

 

 

 

 

A true statement results when the values v = 49 and a = 1600 are inserted into the equation, so we can be confident that we have solved this problem correctly.

 

One final real world application of radical equations comes from the world of medicine. Before determining the dosage of a drug to give to a patient, doctors will sometimes calculate the patient’s Body Surface Area (or BSA). One way to determine a person’s BSA is to use the following formula: , where w = weight (in lbs), h = height (in  cm), and BSA is measured in square meters.

 

Gustav weighs 160 pounds and has a BSA of about  m². How tall (in cm) is he?

 

 

We find that Gustav is 180 cm tall (this is about 5 foot 11 inches). Notice how this problem had radicals on both sides of the equation. Squaring both sides eliminated both radicals and made this problem much easier to solve.

 

The Pythagorean Theorem states that in a right triangle, a2 + b2 = c2. Based on this Theorem, which of the following equations is also true?   A)   B)   C)   D)   Show/Hide Answer A) Incorrect. If you square both sides of this equation you arrive at a2 = b2 - c2. Adding c2 to both sides gives you a2 + c2= b2 which is a different relationship than is modeled in the Pythagorean Theorem. The correct answer is C) .   B) Incorrect. If you square both sides of this equation you arrive at b2 = a2 + c2, which is a different relationship than is modeled in the Pythagorean Theorem. The correct answer is C) .   C) Correct. Taking the square root of both sides of the Pythagorean Theorem will result in this value for c.   D) Incorrect. This equation is not related to the Pythagorean Theorem at all. The correct answer is C) .

 

 

 

A number of real world problems can be modeled with radical equations. When faced with a problem where a variable appears underneath a radical, raise both sides to the same power to remove the radical, and then solve for the variable.