Resolviendo Sistemas de Ecuaciones Lineales por Medio de Gráficas
Objetivos de Aprendizaje
· Describir la creación y el uso de sistemas de ecuaciones.
· Graficar un sistema de ecuaciones lineales en el eje de coordenadas e identificar su solución.
Introducción
A veces, graficar una sola ecuación lineal es todo lo que se necesita para resolver un problema matemático. Otras veces, una sola línea simplemente no nos sirve, y se necesita una segunda ecuación para modelar la situación. Este es normalmente el caso cuando un problema tiene dos variables. Resolver este tipo de problemas requiere trabajar con un sistema de ecuaciones, el cual es un conjunto de dos o más ecuaciones que contienen las mismas incógnitas.
Estudiemos los sistemas de ecuaciones, para ver qué nos revelan las gráficas de ecuaciones individuales sobre la relación matemática entre las variables.
Un sistema de ecuaciones contiene dos o más ecuaciones lineales que comparten dos o más incógnitas. Para encontrar la solución de un sistema de ecuaciones, debemos encontrar un valor (o rango de valores) que satisfagan todas las ecuaciones en el sistema.
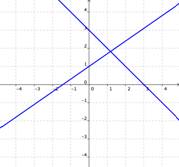
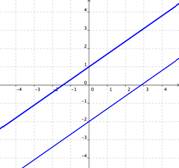
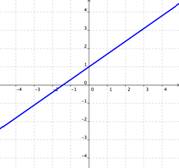
Las gráficas de ecuaciones del sistema nos pueden decir cuántas soluciones existen en ese sistema. Ve las imágenes abajo. Cada una muestra dos rectas que conforman un sistema de ecuaciones (en la gráfica de la derecha las dos rectas se enciman y parecen una sola línea). ¿Cuántos puntos en común revelan cada uno de los sistemas?
| Una Solución | Sin Solución | Soluciones Infinitas |
|
|
|
|
| Si las gráficas de las ecuaciones se intersectan, entonces existe sólo una solución para las ecuaciones.
| S las gráficas de las ecuaciones no se intersectan, (por ejemplo, si son paralelas), entonces no existe ninguna solución para las ecuaciones. | S las gráficas de las ecuaciones son la misma, entonces hay un número infinito de soluciones para las ecuaciones. |
Recuerda, la gráfica de una recta representa cada punto que es una posible solución para la ecuación de dicha recta. Por lo que cuando las gráficas de dos ecuaciones se cruzan, el punto de intersección es común en ambas rectas, lo que significa que es una posible solución para ambas ecuaciones. Cuando las gráficas de dos ecuaciones nunca se tocan, no hay puntos comunes y no hay soluciones posibles para el sistema. Cuando las gráficas de dos ecuaciones quedan una encima de la otra, comparten todos sus puntos y cada uno de ellos es una posible solución.
Graficar ecuaciones para identificar y especificar un punto específico de intersección generalmente no es una forma precisa de resolver sistemas porque podría ser difícil encontrar exactamente el punto donde las rectas se intersectan (a menos que estés usando un programa de computadora que te permita ampliar el punto). Sin embargo, la gráfica de un sistema de ecuaciones puede darnos una idea de qué tipo de solución buscamos. Grafiquemos un sistema, y veamos cómo funciona.
Graficar el sistema y = 3x y x + 2y = 4. ¿Cuántas soluciones tiene este sistema?
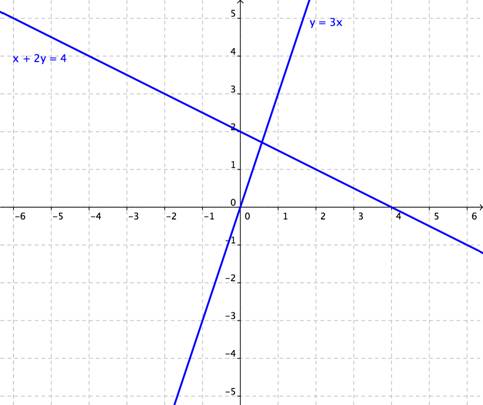
Una gráfica de las dos rectas y = 3x y x + 2y = 4 nos muestra que las rectas se intersectan, lo que significa que existe un único punto (x, y) que satisface ambas ecuaciones. Observa que la gráfica no nos dice exactamente dónde está dicho valor, pero no necesitamos saber esa información, porque sólo nos han preguntado por el número de soluciones.
Entonces un sistema hecho por dos rectas que se intersectan tiene una solución. Ahora veamos una situación distinta:
¿Cuántas soluciones existen para el sistema y -0.5x = 7 y 2y = x − 3?
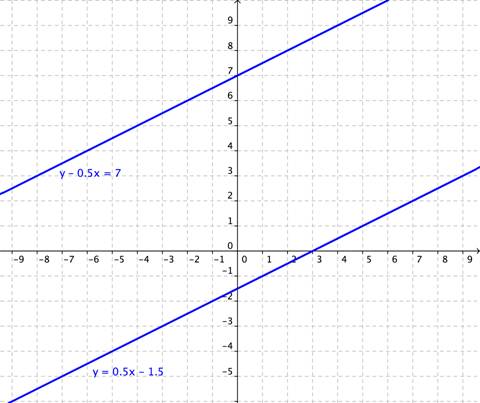
Graficamos ambas ecuaciones y observamos que no hay solución — las rectas son paralelas. Para confirmar nuestro resultado, podemos comparar las pendientes de las ecuaciones. Para hacerlo más fácil, convertimos las ecuaciones a su forma pendiente-intersección o y = mx + b. Lo que nos da las ecuaciones y = 0.5x + 7 y y = 0.5x − 1.5. Sí, la pendiente de ambas rectas es 0.5, lo que significa que las rectas son definitivamente paralelas. Nunca se intersectas, por lo que no hay un punto que sea común a ambas y no hay solución al sistema.
Micaela está tratando de encontrar el número de soluciones posibles para un sistema de dos ecuaciones lineales. Ella dibuja la siguiente gráfica, la cual muestra parte de las dos rectas del sistema. ¿Qué puede concluir?
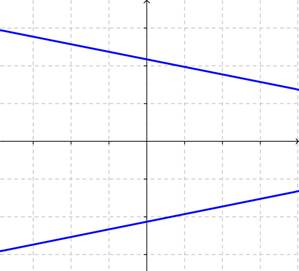
A) El sistema no tiene solución.
B) El sistema tiene una solución.
C) El sistema tiene dos soluciones.
D) El sistema tiene soluciones infinitas.
Graficando un Contexto del Mundo Real
Los sistemas podrían escribirse de manera distinta cuando tratamos con situaciones cotidianas, pero la solución del sistema debe seguir siendo un conjunto de valores que satisfacen todas las ecuaciones. Usemos un ejemplo de basquetbol para explorar un sistema de ecuaciones.
En el partido de basquetbol de ayer, Cheryl anotó 17 puntos con una combinación de canastas de 2 y de 3 puntos. El número de tiros de 2 puntos que ella anotó es mayor que el número de tiros de 3 puntos. ¿Cuántas canastas de cada tipo anotó Cheryl?
En este problema, existen dos relaciones que comparten un conjunto de incógnitas comunes. Podemos pensar en la primera relación como "el número de puntos que anotó Cheryl = el número de tiros de 2 + el número de tiros de 3." La otra relación es "(número de tiros de 2) − 1 = número de tiros de 3.” Nota que en ambas relaciones, las dos incógnitas son la misma: el número de tiros de 2, y el número de tiros de 3.
Relación 1: El número de puntos anotados por Cheryl = el número de tiros de 2 + el número de tiros de 3
Relación 2: (El número de tiros de 2) − 1 = el número de tiros de 3
Empecemos con la primera relación. Sabemos que Cheryl anotó 17 puntos, por lo que podemos incluir eso en la parte izquierda de la ecuación. Ahora tenemos que encontrar algunas combinaciones de tiros de 2 y tiros de 3 que sumados nos resulten 17 puntos. Podemos usar una simple tabla para representar las posibilidades:
| Número Total de Puntos | Número de tiros de 2 | Número de tiros de 3 |
| 17 | 7 (14 puntos) | 1 (3 puntos) |
| 17 | 4 (8 puntos) | 3 (9 puntos) |
| 17 | 1 (2 puntos) | 5 (15 puntos) |
Entonces, para la primera relación, existen tres posibles soluciones. Cheryl pudo haber anotado 17 puntos con cualquiera de las combinaciones de la tabla. Aquí está una gráfica que muestra las posibles soluciones para la primera relación:
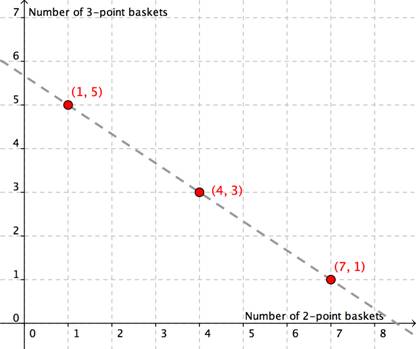
Ahora consideramos la segunda relación. El número de tiros de 2 es mayor que el número de tiros de 3 que ella anotó. Podemos también hacer una tabla que represente esta información.
| Número de tiros de 2 | Número de tiros de 3 |
| 1 | 0 |
| 2 | 1 |
| 3 | 2 |
| 4 | 3 |
| 5 | 4 |
| … | … |
Nota que esta relación podría continuar indefinidamente porque la ecuación no especifica un límite de cuantas canastas anotó Cheryl.
Como las variables de esta relación son las mismas que las de la primera relación, podemos graficarlas en el mismo eje de coordenadas:
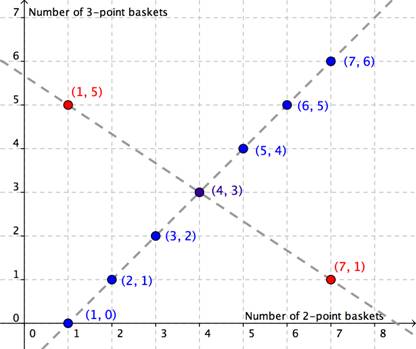
¿Qué es lo que observamos? Tenemos dos ejes, uno llamado "número de tiros de 2" y el llamado "número de tiros de 3," y hemos graficado ambas relaciones sobre estos ejes. Existe un solo punto común a las dos rectas que satisface ambas ecuaciones. Ese punto es (4, 3), y es la solución del sistema: Cheryl anotó 4 canastas de 2 puntos y 3 canastas de 3 puntos.
¿Cuál de los siguientes escenarios sólo puede ser solucionado usando un sistema de ecuaciones?
A) Paco y Lisel gastaron $30 en el cine ayer en la noche. Hoy, gastarán otros $10 en la cena. ¿Cuánto gastaron en total?
B) Paco y Lisel gastaron $30 en el cine ayer en la noche. Les sobraron $8. ¿Cuánto dinero tenían antes de ver la película?
C) Paco y Lisel gastaron $30 en el cine ayer en la noche. Cada boleto costó $9. ¿Cuánto gastaron en el refresco y las palomitas?
D) Paco y Lisel gastaron $30 en el cine ayer en la noche. Paco gastó $8 más que Lisel. ¿Cuánto gastaron cada uno?
Sumario
Un sistema de ecuaciones es aquel que está compuesto de dos o más ecuaciones que comparten dos o más incógnitas. Podemos graficar las ecuaciones del sistema para averiguar si el sistema tiene cero soluciones (representado por rectas paralelas), o una solución (representado por rectas que se intersectan), o si hay un número infinito de soluciones (representado por dos rectas superpuestas) A pesar de que las gráficas de sistemas de ecuaciones son una técnica útil, no son siempre una forma precisa de encontrar la solución a un sistema de ecuaciones.