Point Slope Form and Standard Form of Linear Equations
Learning Objective(s)
· Give the point slope and standard forms of linear equations and define their parts.
· Convert point slope and standard form equations into one another.
· Apply the appropriate linear equation formula to solve problems.
Introduction
Linear equations can take several forms, such as the point-slope formula, the slope-intercept formula, and the standard form of a linear equation. These forms allow mathematicians to describe the exact same line in different ways.
This can be confusing, but it’s actually quite useful. Consider how many different ways you could write a request for milk on a shopping list. You could ask for white milk, cow’s milk, a quart of milk, or skim milk, and each of these phrases would describe the exact same product. The description you use will depend on the characteristics that matter most to you.
Equations for describing lines can be chosen the same way—they can be written and manipulated based upon on which characteristics of the line are of interest. Even better, when a different characteristic becomes important, linear equations can be converted from one form to another.
One type of linear equation is the point slope form, which gives the slope of a line and the coordinates of a point on it. The point slope form of a linear equation is written as ![]() . In this equation, m is the slope and (x1, y1) are the coordinates of a point.
. In this equation, m is the slope and (x1, y1) are the coordinates of a point.
Let’s look at where this point-slope formula comes from. Here’s the graph of a generic line with two points plotted on it.
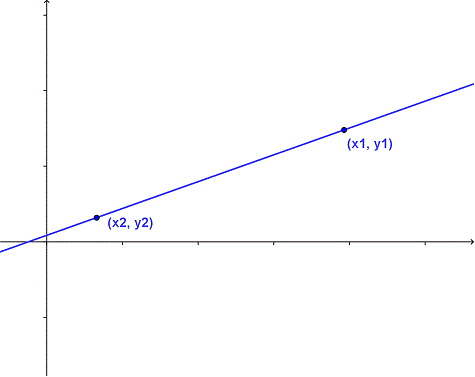
The slope of the line is “rise over run.” That’s the vertical change between the two points (the difference in the y-coordinates) divided by the horizontal change over the same segment (the difference in the x-coordinates). This can be written as ![]() . This equation is the slope formula.
. This equation is the slope formula.
Now let’s say that one of these points is a generic point (x, y), which just means it could be anywhere on the line, and the other point is a specific point, ![]() . If we plug these coordinates into the formula, we get
. If we plug these coordinates into the formula, we get ![]() . Now we can rearrange the equation a little bit by multiplying both sides of the formula by
. Now we can rearrange the equation a little bit by multiplying both sides of the formula by ![]() . This simplifies to
. This simplifies to ![]() .
.
![]()
![]()
![]()
![]()
![]() is the point-slope formula. We’ve converted the slope formula into the point slope formula. We didn’t do that just for fun, but because the point slope formula is sometimes more useful than the slope formula, for example when we need to find the equation of a line when given a point and the slope.
is the point-slope formula. We’ve converted the slope formula into the point slope formula. We didn’t do that just for fun, but because the point slope formula is sometimes more useful than the slope formula, for example when we need to find the equation of a line when given a point and the slope.
Let’s do an example. Consider a line that passes through the point (1, 3) and has a slope of ![]() .
.
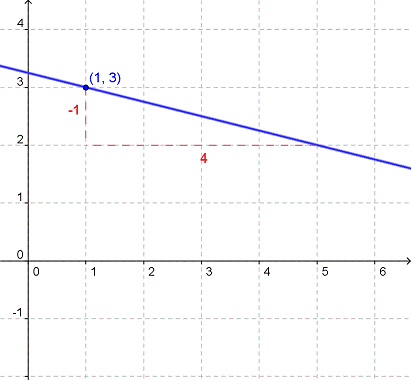
Putting these values into the point-slope formula, we get ![]() . That’s the equation of the line.
. That’s the equation of the line.
Which of the following points lies on the line (y + 8) = 7(x − 5)?
A) (5, -8)
B) (5, 8)
C) (8, 5)
D) (8, -5)
Remember, the point-slope formula is only one type of linear equation. It is effective in describing some of the characteristics of a straight line. However, point slope equations can be awkward to use in some algebraic operations. In such cases, it may be helpful to convert the equation into a different form, the standard form.
The standard form of an equation is Ax + By = C. In this kind of equation, x and y are variables and A, B, and C are integers.
We can convert a point slope equation into standard form by moving the variables to the left side of the equation. Let’s go back to that point-slope equation of ![]() . We can rearrange the terms as follows:
. We can rearrange the terms as follows:
| Example | |||
|
Problem |
(y − 3) |
= |
|
|
|
4(y − 3) |
= |
|
|
| 4y − 12 | = | -1x + 1 |
|
| x + 4y − 12 | = | -x + 1 + x |
|
| X + 4y − 12 | = | 1 |
|
| x + 4y − 12 + 12 | = | 1 + 12 |
| Standard Form | x + 4y | = | 13 |
When we shift the variable terms to the left side of the equation and everything else to the right side, we get ![]() . This equation is now in standard form.
. This equation is now in standard form.
We now know how to convert equations from point slope to standard form, and how to go back and forth between a graph and a linear equation. But with so many choices, how do we decide which form to use in a real-life situation?
The answer is to identify what you know and what you want to find out, and see which form uses those terms. Let’s look at a situation where one form of an equation is more useful than the others.
Andre wants to buy an MP3 player. He got $50 for his birthday, but the player he wants costs $230, so he’s going to have to save up the rest. His plan is to save $30 a month until he has the money he needs. We’ll help him out by writing an equation to analyze this situation. This will help us to figure out when he will have saved up enough to buy the MP3 player.
When we write the equation, we’ll let x be the time in months, and y be the amount of money saved. After 1 month, Andre has $80. That means when x = 1, y = 80. So we know the line passes through the point (1, 80). Also, we know that Andre hopes to save $30 per month. This means the rate of change, or slope, is 30.
We have a point and we have a slope—that’s all we need to write a point slope formula, so that’s the form of linear equation we’ll use. Remember, the point slope form is ![]() . When we substitute in Andre’s point and slope, the equation becomes
. When we substitute in Andre’s point and slope, the equation becomes ![]() .
.
Okay, now what? Well, we have a formula that describes Andre’s savings plan. We can use that to figure out how long it will take him to save all the money he needs to buy the MP3 player.
Remember, the y in this equation represents the amount Andre has saved, and the x represents the number of months he has been saving. We want to find what the value of x is when y equals 230. So we just need to set y equal to 230 in our equation, and solve for x.
| Example | |||
| Problem | y − 80 | = | 30(x − 1) |
|
| 230 − 80 | = | 30(x − 1) |
|
| 150 | = | 30x − 30 |
|
| 180 | = | 30x |
| Answer | 6 | = | x |
The result is x = 6. It will take Andre 6 months to save the $230 he needs to buy the MP3 player. Because the problem told us that we knew a point and a slope, we were able to choose the right form for the job of writing an equation. Once we wrote the equation, we were able to solve it for the variable we wanted to find.
Summary
We’ve learned that linear equations can be written in different forms, depending upon what we either know or want to know about a line. The point slope form, ![]() , is useful in situations involving slope and the location of one or more points. The standard form, Ax + By = C, is usually easier to use when we need to make algebraic calculations. When needs or knowledge change, we can convert an equation from one form into another.
, is useful in situations involving slope and the location of one or more points. The standard form, Ax + By = C, is usually easier to use when we need to make algebraic calculations. When needs or knowledge change, we can convert an equation from one form into another.
