Funciones no Lineales
Objetivos de Aprendizaje
· Definir las funciones no lineales.
· Definir las funciones inversas y reconocerlas en forma de ecuación, tabla y gráfica.
· Definir las funciones cuadráticas y reconocerlas en forma de ecuación, tabla y gráfica.
· Definir las funciones exponenciales y reconocerlas en forma de ecuación, tabla y gráfica.
¿Alguna vez has cocinado galletas? No las puedes tocar cuando apenas han salido del horno, o te quemarás. No toma mucho tiempo para que se enfríen lo suficiente para que las puedas comer, pero se mantienen templadas por mucho tiempo. Y no se enfrían más que la temperatura ambiente. Si dibujamos una gráfica del enfriamiento de una galleta, se vería más o menos así:
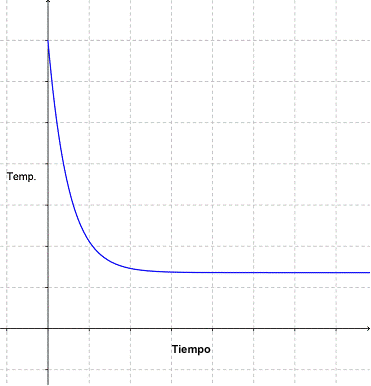
Nota que la gráfica está muy empinada al principio y luego se nivela con el pasar del tiempo, hasta que las galletas están a temperatura ambiente. Esta es una función — hay una entrada y una salida, y al cambiar el tiempo (la entrada), también cambia la temperatura (la salida). Pero no es una función lineal, porque no sigue una línea recta. Una función que no es lineal se llama función no lineal — ¡Seguro es fácil de recordar!
Hay muchos tipos de funciones no lineales. Vamos a explorar sólo algunos de ellos.
Un tipo de función no lineal se llama variación inversa. En éstas funciones, la variable dependiente es igual a una constante multiplicada por la inversa de la variable independiente. En forma simbólica, ésta es la ecuación 
, donde y es la variable dependiente, k es la constante, y x es la variable independiente. Compárala con la ecuación para una función que tiene variación directa entre las variables, como la función proporcional con fórmula 
. La única diferencia es que se utiliza la inversa de la entrada.
Un ejemplo de una función inversa es la velocidad requerida para viajar entre dos ciudades en un lapso de tiempo dado.
Digamos que necesitas conducir desde Boston hasta Chicago, que son aproximadamente 1,000 millas. Entre más tiempo tienes, más lento puedes ir. Si quieres llegar en 20 horas, necesitas ir a 50 millas por hora, porque 
. Pero si dispones de 40 horas para llegar, sólo tienes que promediar 25 millas por hora, ya que 
. La ecuación para averiguar qué tan rápido debes conducir dada una cantidad de tiempo es 
, o 
. Si te fijas, ésta es la misma forma que la fórmula de la función de variación inversa, .
Aquí está una tabla que muestra diferentes tiempos y velocidades que satisfacen la ecuación:
| Tiempo | Velocidad (millas por hora) |
| 1 | 1,000 |
| 5 | 200 |
| 10 | 100 |
| 15 | 66 2/3 |
| 16 | 62 1/2 |
| 20 | 50 |
| 40 | 25 |
Ahora, si graficamos esos puntos, veremos que la gráfica no es una línea recta.
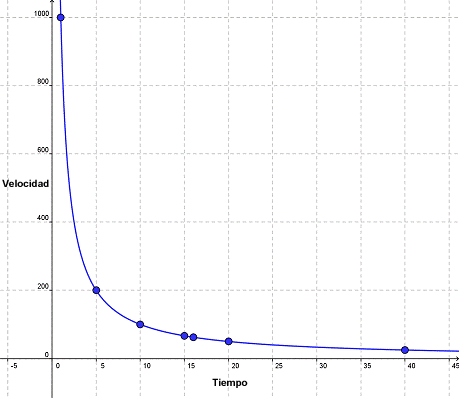
Una parte importante de las funciones y sus gráficas es la tasa de cambio. ¿Qué está pasando con la tasa de cambio en ésta gráfica? Cuando el tiempo está cerca de 0, un pequeño cambio en el tiempo produce una caída significante en la tasa en el que necesitas conducir. Si tienes muy poco tiempo, digamos 1 hora, tendrías que viajar a 1000 millas por hora para lograrlo, y creo que eso es ilegal. Pero si tienes disponible tan sólo otra hora más, puedes reducir la velocidad a 500 millas por hora.
Ahora mira el centro de la gráfica. La gráfica se vuelve plana — el cambio de una hora no provocará mucha diferencia en la velocidad. Si tú manejas por 15 horas, necesitarás ir a casi 67 mph, Añade una hora extra y ésta vez la velocidad requerida cae a sólo 4 millas por hora.
La tasa de cambio en ésta gráfica no es constante. Empieza muy alto, y la gráfica es muy empinada. Pero conforme la tasa de cambio disminuye, la gráfica se nivela.
En una función inversa, ¿qué le pasa a la salida cuando el valor de la entrada se reduce?
Otro tipo de función no lineal es la función cuadrática. En una función cuadrática, la variable independiente (x) se multiplica a sí misma.
Veamos la función cuadrática más simple, que tiene la ecuación y = x2. Una tabla de valores de x y y de ésta función se vería así:
| x | y |
| -3 | 9 |
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
En una gráfica, estos valores forman una línea curva con forma de U llamada parábola.
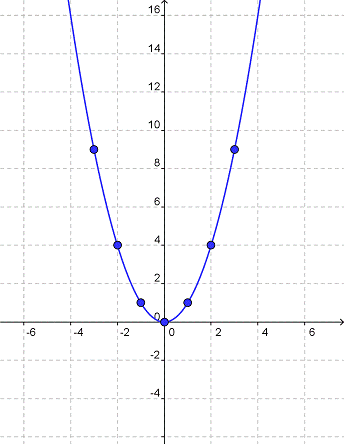
Todas las funciones cuadráticas forman una parábola en una gráfica. La parábola puede abrir hacia arriba (así – U) o hacia abajo (así – ∩). Puede ser amplia o angosta, simétrica sobre el eje y o acostada en uno de los cuadrantes. Las funciones cuadráticas son usadas para describir cosas con curvas simétricas suaves, como el botar de una pelota o el arco de un puente.
Una función cuadrática puede tener la ecuación y = x2. Pero otras fórmulas de funciones cuadráticas son más complejas — éstas son llamadas ecuaciones cuadráticas:
| y = ax2 + bx + c |
| y = (ax + b)(cx + d) |
| y = a(x+b)2 + c |
Lo importante que hay que notar es que en cada ecuación, la variable independiente está multiplicada por sí misma. Las letras a, b, c y d son coeficientes — su presencia en la ecuación modifica la silueta y localización de la parábola.
¿Confundido? Intenta esto — la gráfica interactiva de abajo te permite cambiar los valores de a, b, c y d en la fórmula estándar de la ecuación cuadrática y = ax2 + bx + c. Haz clic y arrastra los controles deslizantes llamados a, b, c y para ver qué pasa con la parábola.
La gráfica de abajo muestra la función de la altura contra el tiempo de una pelota que lanzas al aire y la atrapas.
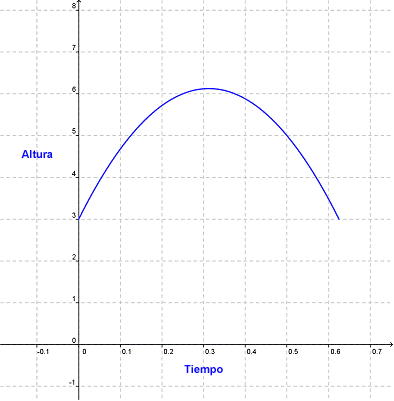
Basado en la gráfica, ¿cuál de las siguientes declaraciones es verdadera?
A) Entre más alta está la pelota, más lentamente se mueve.
B) La pelota viaja a una velocidad constante.
C) La pelota se eleva más rápido de lo que cae.
D) La pelota cae más rápido de lo que se eleva.
Otro tipo de función no lineal es la función exponencial. En éstas funciones, la variable independiente es un exponente en la ecuación. La fórmula de la función exponencial tiene la forma y = abx. Como x es el exponente, si b es mayor que 1, la salida crecerá muy rápido por cada pequeño incremento del valor de entrada. Las funciones exponenciales son usadas en cosas relacionadas con el crecimiento o la disminución de una población o la descomposición radiactiva.
Aquí hay una tabla que muestra los valores de x y y para la ecuación y = 2x.
| x | y |
| -2 | 0.25 |
| -1 | 0.5 |
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
La gráfica de ésta función se ve así:
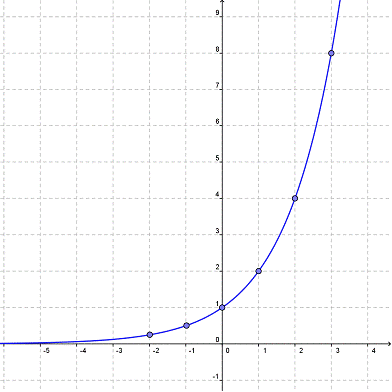
Puedes ver por qué el término matemático "exponencial" se ha vuelto popular para describir cambios rápidos y explosivos.
Las letras a y b en la ecuación de la función exponencial son coeficientes que forman la base del exponente x. Esta gráfica interactiva te permite manipular los valores de la ecuación y = abx. Haz clic y arrastra los controles deslizantes llamados a y b y nota el gran efecto que provocan pequeños cambios. En las funciones exponenciales, poco significa mucho.
Sumario
Hemos explorado algunos tipos de funciones no lineales. Como las funciones lineales, las funciones relación inversa, cuadrática y exponencial nos pueden ayudar a modelar situaciones del mundo real y entenderlas mejor. A diferencia de las funciones lineales, la tasa de cambio en las funciones no lineales no es constante sino que varía. Debido a esto, las gráficas de funciones no lineales muestran líneas curvas.
