Absolute Value

 

Learning Objective(s)

·         Find the absolute value of numbers and expressions.

·         Represent absolute values with numerical statements and on number lines.

 

Introduction

 

Algebra usually requires us to be careful about not just the size of a value but also its sign.  -10 is different than 10.  3 + 7 yields a different result than 3 + (-7). But there are circumstances in which the sign doesn’t matter, in mathematics and in real life. Have you ever stumbled stepping on or off a moving walkway? It doesn’t really matter if you’re moving faster or slower than the ground surface—it’s the magnitude of the difference that makes you lose your balance. Or think of taking a long hike—your feet will get just as sore whether you go north or south. Direction doesn’t matter, only distance.

 

In mathematics, there’s a concept for dealing with situations where size matters more than sign. It’s called absolute value. The absolute value of a number is its value regardless of its sign.

 

Absolute Value—the Numeric Approach

 

Absolute value can be explored both numerically and graphically. Numerically, absolute value is indicated by enclosing a number, variable, or expression inside two vertical bars, like so:

 

|20|

|x|

|4n − 9|

 

When we take the absolute value of a number, it is always either positive or zero. If the original value is already positive or zero, the absolute value is the same. If the original value is negative, we simply drop the sign.  For example, the absolute value of 5 is 5. The absolute value of -5 is also 5.

 

Example

 

Value

Absolute Value

5

5

-5

5

 

Remember, in absolute value situations we aren’t changing the location or direction of a number, we’re just ignoring those details.

 

Be careful not to confuse |absolute value bars| with (parentheses) or [brackets]. They are not the same symbols, and different rules apply for evaluating them.

 

For example, -1(-3) = 3. The negatives inside and outside the parentheses cancel out when they are multiplied.

 

Example

Problem

-1(-3)

=

 

 

-1 • -3

=

3

 

But -1|-3| = -3. You can't multiply across the absolute value bars, so you must first find the absolute value of the number inside them. Since the absolute value of -3 is 3, the operation becomes -1(+3).

 

Example

Problem

-1|-3|

=

 

 

-1 • 3

=

-3

 

When absolute value bars enclose an expression that includes operations, the expression must be evaluated before finding the absolute value. Consider the expression |6 − 4|. Before we can take the absolute value of the expression, we need to carry out the subtraction. When we do that, |6 − 4| becomes |2|.  Now we can find the absolute value of the expression—it's the absolute value of 2, which is 2.

 

|6 − 4| = |2| = 2

 

Similarly, for the expression |15 − 21|, we must carry out the operations inside the absolute value bars first.

 

|15 − 21| = |-6| = 6

 

Which of the following is the correct value of |6 − 9|?

 

A) -3

B) 3

C) (-3)

D) 15

 

Show/Hide Answer

A) -3

Incorrect. The absolute value of a number is always positive or zero. If the original number is negative, its absolute value is that number without the negative sign. The correct answer is 3.

 

B) 3

Correct. |6 − 9| = |-3| = 3.

 

C) (-3)

Incorrect. |6 − 9| = |-3|. The absolute value bars are not the same as parentheses. The correct answer is 3.

 

D) 15

Incorrect. 15 is 6 + 9. We must perform the operation inside the bars before we drop the negative sign. |6 − 9| = |-3| = 3. The correct answer is 3.

 

 

Absolute Value—the Graphic Approach

 

On a number line, the absolute value of a number or expression is the distance between the value and zero. When using a number line to explore absolute value, the absolute value of an expression will always lie at zero or to the right of zero. If the original value is positive or zero, the absolute value will overlie the original.

 

If we plot both the original value and the absolute value, they are in the same place. The |3| is 3. In this case, both the original value and the absolute value lie 3 units to the right of zero on a number line.

 

 

 

If the original value is negative, the absolute value will lie at the same distance from zero as the original, but on the other side of the origin. The |-4| is 4. If we plot both original and absolute values, they are the same distance from zero, but in opposite directions.

 

 

 

When using a number line to show the absolute value of an expression, we must once again be sure to carry out all of the operations inside the bars before plotting. The |4 − 6| is plotted at 2, not -2, 4, or 6.

 

Which of the points on this number line is |3 − 8|?

 

 

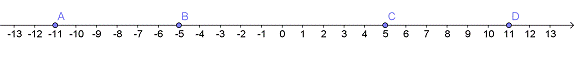
A) point D

B) point A

C) point B

D) point C

 

Show/Hide Answer

A) point D

Incorrect. 11 is |3 + 8|, not |3 − 8|. |3 − 8| = |-5|. The absolute value of -5 is 5. The correct answer is point C, 5.

 

B) point A

Incorrect. -11 is -|3 + 8|, not |3 − 8|. |3 − 8| = |-5|. The absolute value of -5 is 5. The correct answer is point C, 5.

 

C) point B

Incorrect. -5 is the value of 3 − 8, not the absolute value. The absolute value of a negative number is that same number without the − sign. The correct answer is point C, 5.

 

D) point C

Correct. |3 − 8| = |-5|. The absolute value of -5 is 5.

 

 

Summary

 

Absolute value is a helpful concept when we are only interested in the size of the difference between two numbers. Absolute value gives distance, but discards information about direction. Because direction is ignored, the absolute value of any number can only be positive or zero, never negative. When an expression’s value is positive or zero, its absolute value is the same as the initial value. When the value of an expression is negative, its absolute value is that same value with the negative signed dropped.